1 Innledning
1.1 Generatoren - en energiomformer 1.2 Generatorens plass i produksjonssystemet for elektrisk kraft.2 Generelle prinsipper
2.1 Magnetisk fluks og induksjon. 2.2 Induksjonsloven. 2.3 Roterende sløyfe i konstant, magnetisk felt. 2.4 Magnetisk motstand og -potensial 2.5 Viserdiagrammer.3 Synkronmaskinens virkemåte
3.1 To-polet, enfase synkronmaskin. 3.2 To-polet, trefase synkronmaskin. 3.3 Poltall - Turtall 3.4 Polskoformer. Grunnharmonisk felt. 3.5 Forkortet skritt. Skrittforkortningsfaktor. 3.6 Fordelte viklinger. Viklingsfordelingsfaktor. 3.7 Statorviklinger. Praktisk utforming. 3.8 Beregning av klemmespenning.4 Generelle utleggingsprinsipper
4.1 Utnyttelse. 4.2 Svingmasse. 4.3 Bestemmelse av hoveddimensjoner. 4.4 Eksempel.5 Typiske byggeformer
5.1 Langsomtløpende generatorer. 5.2 Hurtigløpende generatorer 5.3 “Størrelse” og “teknologi”HÅNDBOK - GENERELT OM VANNKRAFTGENERATORER
Teoretisk bakgrunn, grunnleggende dimensjonering, unormale driftspåkjenninger, aldring/ levetid
Hensikt/ Innhold:
• Friske opp kunnskapen innen elektromagnetisk teori for elektriske maskiner
• Etablere forståelse for grunnleggende prinsipper innen utlegging og dimensjonering av generatorer
• Gi en oversikt over typiske byggeformer og gjennomgå deres typiske egenskaper
• Gi en oversikt over unormale driftspåkjenninger og deres konsekvenser
• Gi en oversikt over historiske utviklingstrekk innen materialer og framstillingsmetoder innen produksjon av generatorer
• Gi innledende kommentar til emnet “Aldring/ Levetid”
1 Innledning
1.1 Generatoren - en energiomformer
De fleste av oss tenker vel på generatoren som på en maskin som går rundt og lager strøm. Selve ordet generator kommer av verbet generere som betyr frambringe eller produsere. En elektrisk generator skulle da være en innretning som produserer elektrisk strøm.
Noe mer presist kan vi si at en generator er en “Energiomformer” som omformer energi av en kategori, nemlig bevegelsesenergi, til en annen kategori, nemlig elektrisk energi.
I vår moderne tilværelse er vi omgitt av forskjellige typer energiomformere på nær sagt alle områder som for eksempel på bilen der den potensielle energien i bensinen via varme blir omformet til den ønskede bevegelsesenergi, eller varmeovnene og komfyren eller lyspærene hjemme der elektrisk energi blir omformet til varme- og lys-energi.
Eller vi kan tenke oss stereoanlegget i stua som tapper elektrisk energi ut av stikkontakten og omformer den til bevegelsesenergi i høyttalermembranene i takt med signalene på plata eller magnetbåndet.
Felles for alle energiomformere er at de har en inngang der en tilfører energi av en bestemt kategori, og en utgang der en får ut den ønskede energiform.
Dessuten er det slik at den energimengden vi får ut fra en omformer aldri kan bli større enn den energimengden som mates inn. Tvert imot er den noe mindre.
Differansen skyldes omformingsprosessens energiforbruk, dvs. at noe av den tilførte energien blir omdannet til andre former for energi som ikke når utgangen. Dette er et uønsket biprodukt som vi har mistet på veien og som vi derfor betegner med ” Tap”. Siden denne “tapte” energien ofte er varmeenergi, snakker vi gjerne om “Tapsvarme”. Denne må vi sørge for blir ledet bort fra omformeren. Dersom vi ikke gjør det, vil den akkumuleres i omformeren og temperaturen vil stige og stige.
1.2 Generatorens plass i produksjonssystemet for elektrisk kraft.
I vårt land utgjør elektrisk energi en vesentlig del av det totale energiforbruk. Ser vi på forbruket av elektrisk energi pr. innbygger, topper Norge verdensstatistikken. (Hvis vi imidlertid ser på det totale energiforbruk pr. innbygger, kommer vi lengre ned på listen.)
Hos oss blir så godt som 100 % av den elektriske energien
produsert ved vannkraft. I omformings-prosessen fra den
potensielle energi i vannet til den elektriske energi som kan tas
ut av stikkontakten på veggen hjemme, inngår en rekke typer
energiomformere. (Se Figur 1
og Figur 2)
Vannmagasinet er i besittelse av en potensiell energimengde som
er proporsjonal med produktet av utnyttbar fallhøyde og
vannmengden i magasinet. I vannveien som fører ned til turbinen
blir høydepotensialet omformet til trykkpotensial samt noe
hastighetspotensial. Når vannet strømmer inn i turbinhjulet, blir
en potensielle energien omdannet til bevegelsesenergi. Denne blir
så mekanisk overført til generatoren via turbinhjul og aksel.
Generatoren omformer den tilførte bevegelsesenergi til elektrisk energi med en passe spenning for generatoren. (Se Figur 2)
Når en skal overføre store energimengder over lange strekninger, vil det være hensiktsmessig å heve spenningen mest mulig for å redusere overføringstap. Den optimale spenning vil imidlertid også være en balanse mellom kostnaden på akive deler (Kobber, aluminium) og kostnaden på passive deler. (Isolatorer, master, osv.) Kostnaden for aktive materialer vil nemlig minke med spenningen, mens kostnaden for de passive materialene vil øke med spenningen.
For å oppnå den ønskede spenning, settes det inn en transformator mellom generatoren og overføringslinjen. Transformatoren er i prinsipp også en energiomformer som omformer elektrisk energi med ett spenningsnivå til elektrisk energi med et annet spenningsnivå.
Denne spenningen må vi så transformere ned igjen i ett eller flere trinn til den spenning som forbrukeren skal ha.
2 Generelle prinsipper
I generatoren utnytter vi det fenomen at om en elektrisk leder beveger seg i et magnetisk felt, så vil det induseres en elektrisk spenning over lederen. (Se Figur 3)
Før vi ser nærmere på dette, skal vi først repetere noen grunnleggende, magnetiske begreper.
2.1 Magnetisk fluks og induksjon.
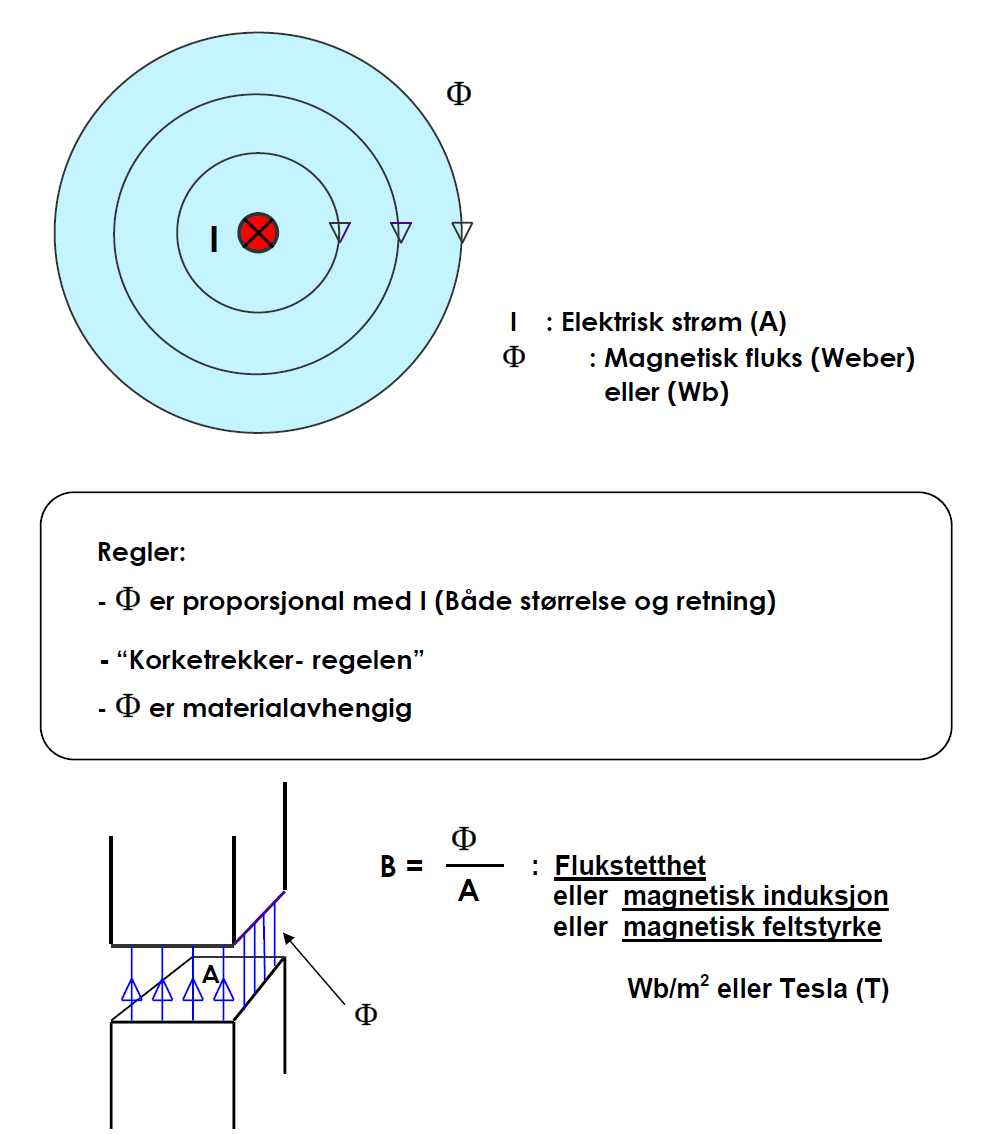
Dersom det flyter en strøm i en leder, vil det oppstå et magnetisk felt rundt lederen. Dette feltet er proporsjonalt med strømmen og betegnes gjerne med den greske bokstaven φ.
Magnetisk fluks angis i enheten “Weber”, forkortes “Wb”.
Vi skal merke oss at dersom strømmen skifter retning, vil også fluksen gjøre det. For å bestemme retningen for fluksen i forhold til strømmen kan vi tenke oss en høyregjenget
skrue som vi skrur til i strømretningen. Rotasjonsretningen for skruen vil da angi retningen på fluksen.
Fluks pr. flateenhet A, kalles flukstetthet, feltstyrke eller induksjon. Betegnelsen er gjerne bokstaven “B” og enheten angis i Wb/m2 eller “Tesla” (forkortet T) som er samme sak.
Dersom flukstettheten er konstant over flaten, blir relasjonen mellom φ og B gitt av følgende uttrykk:
\[B = \phi/A\qquad{(1)}\]
Hvor B = [T], φ = [Wb], A = [m2]
2.2 Induksjonsloven.
Ved å kople et voltmeter over endene på lederen, slik som vist i Figur 3, vil lederen, tilkoplingsledningene og voltmetret utgjøre en lukket sløyfe (vinding).
I en vilkårlig lederstilling flyter det en bestemt magnetisk fluks, φ, gjennom sløyfen. Dersom vi nå beveger lederen, vil fluksen gjennom sløyfen forandre seg. Beveges lederen til venstre på Figur 3, øker fluksen, mens den minker om bevegelsen er til høyre.
Hvis vi beveger lederen fram og tilbake i det konstante magnetfeltet (med lederen hele tiden inne i magnetfeltet), vil vi oppdage følgende:
- Spenningen, U, øker når hastigheten, v, på lederen øker. Ved nærmere undersøkelse viser det seg at spenningen er direkte proporsjonal med hastigheten.
- Spenningen skifter retning når hastigheten på lederen skifter retning. Ved nærmere undersøkelse vil vi finne at retningen av spenningen er slik at den forsøker å drive en strøm, I, i lederen som vil hindre at fluksen i sløyfen forandrer seg.
Dersom lederen beveges mot venstre i Figur 3, vil fluksen gjennom sløyfen øke. Dette vil altså den induserte spenningen i sløyfen prøve å motsette seg. Den vil derfor prøve å drive en strøm som har en slik retning at den fluksen som den er årsak til, prøver å hindre fluksøkningen i sløyfen. Fluksen som strømmen setter opp har altså motsatt retning av den fluksforandring som skyldes bevegelsen av sløyfen. Retningen på strømmen vil dermed bli fra pkt.a til pkt.b i Figur 3 ifølge skrueregelen som vi nevnte ovenfor. Dermed er også spenningsretningen gitt, nemlig + ved pkt.a.
Vi øker nå feltstyrken i sløyfen ved å øke magnetiseringsstrømmen, If . Så beveger vi lederen på samme måten som før og med samme hastighet. Vi legger merke til følgende:
- Spenningen, U, har øket i forhold til tidligere. Ved nærmere observasjon viser det seg at spenningen er proporsjonal med feltstyrken B.
Hvis vi slår sammen alle observasjoner vi har gjort, kan vi forme det til en generell regel på følgende måte:
- Indusert spenning i en sløyfe er proporsjonal med fluksforandringen pr. tidsenhet i sløyfen.
Dette er den grunnleggende regel for all generatorteori og benevnes med “Induksjonsloven”. Matematisk kan denne uttrykkes slik:
\[U = - d\phi/dt\qquad{(2)}\]
Hvor U = Volt [V], dφ = [Wb], dt = sek [s] og dφ/dt angir hvor mye fluksen forandres pr. tidsenhet. Minustegnet sørger for riktig retning på spenningen i forhold til fluksforandringen.
Hvis f.eks. fluksen i en sløyfe forandrer seg med dφ/dt=1 Wb/s, vil den induserte spenningen over sløyfen bli 1 V.
Dersom vi kopler N sløyfer i serie, får vi en spole med N vindinger. Hver vinding vil få en indusert spenning som er gitt av lign. Formel 2. Over spolen blir da spenningen:
\[U = - N \cdot d\phi/dt\qquad{(3)}\]
Lign. Formel 3 representerer induksjonsloven for en spole med N vindinger.
I det foregående har vi sett at vi får indusert en spenning i en sløyfe eller spole ved å bevege den i et magnetisk felt som holdes konstant. Dette kunne vi kalle “bevegelsesindusert spenning”. I en generator går ikke viklingene fram og tilbake, men roterer. Her bruker vi derfor betegnelsen “rotasjonsindusert spenning”.
Induksjonsloven, lign. Formel 3, stiller ikke noe krav til måten vi skaffer oss fluksvariasjonen på. Virkningen blir den samme, enten vi lar en spole bevege seg i et konstant magnetfelt eller varierer feltet i en stillestående spole. Dette siste er det som skjer i en transformator.
Spenningen som induseres på denne måten kaller vi derfor “transformatorisk indusert spenning”.
2.3 Roterende sløyfe i konstant, magnetisk felt.
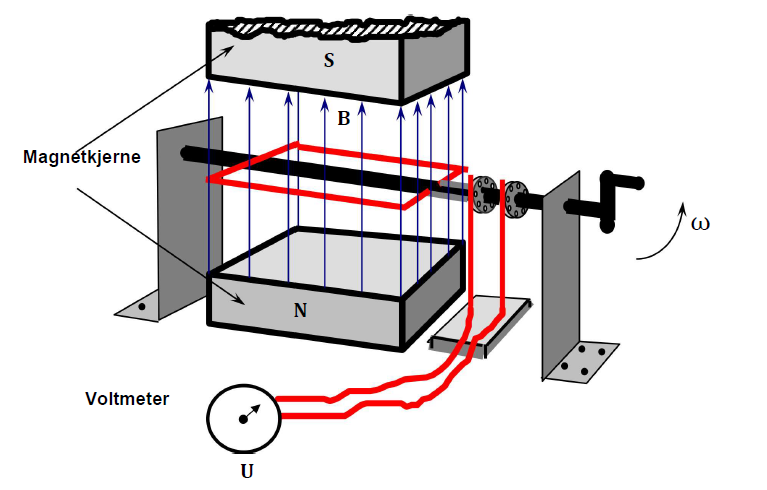
Vi skal nå se litt nærmere på rotasjonsindusert spenning og tenker oss en anordning som vist i Figur 5. Her lar vi en vindingssløyfe rotere mellom en nordpol og en sørpol. Mellom polene er det et magnetisk felt med feltstyrke B. Vi regner at feltet er konstant i hele sløyfens utstrekning.
Sløyfen har et areal, A = b • l, der b er bredden og l er lengden av sløyfen.
Vi vil gjerne finne spenningen over sløyfen uttrykt med feltstyrken, B, sløyfearealet, A, og vinkelhastigheten, ω, som sløyfen roterer med.
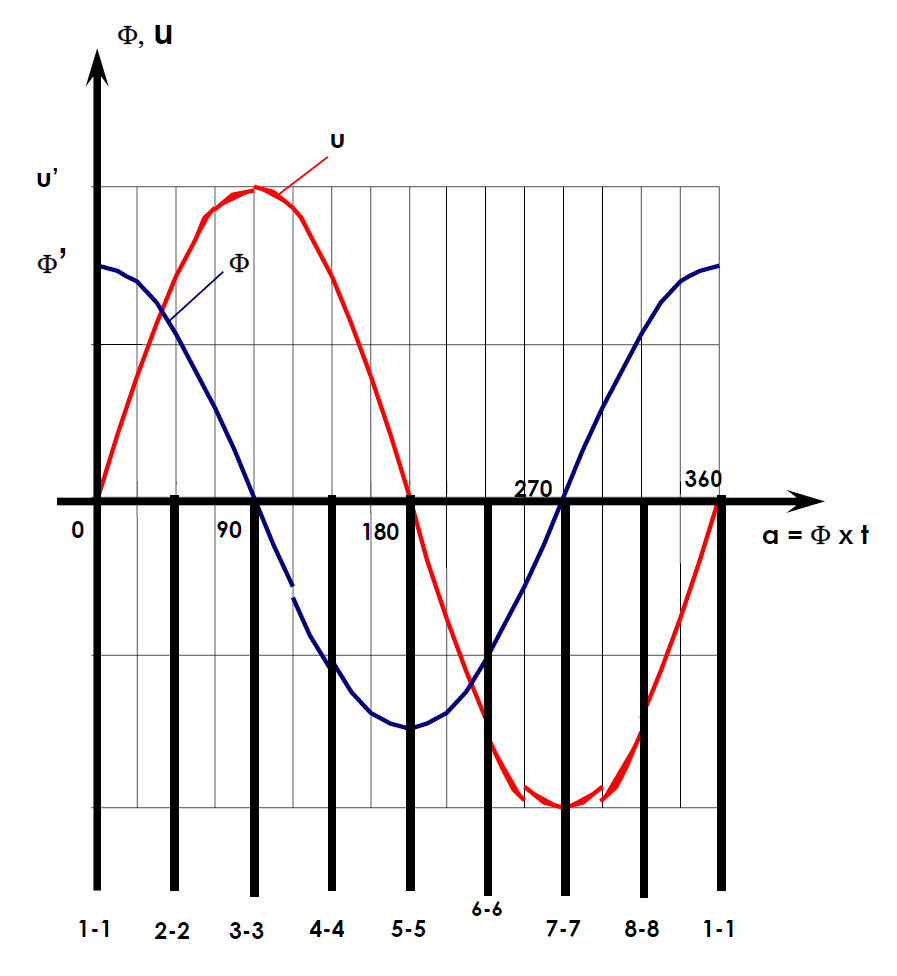
I utgangspunktet ligger sløyfen horisontalt, slik som vist på Figur 6 Dette tilsvarer stilling 1-1 på Figur 6. I denne stillingen flyter det en fluks, φ’ gjennom sløyfen. Vi ser at om vi dreier sløyfen den ene eller den andre veien, vil fluksen gjennom sløyfen minke. φ’ er derfor den maksimale fluksen som sløyfen vil føre hvis feltstyrken, B, holdes konstant.
I stilling 3-3 går det ingen fluks gjennom sløyfen. Vi ser også at i denne stillingen vil retningen av fluksen gjennom sløyfen snu. Hvis vi definerer fluksretningen som positiv før vi når stilling 3-3, vil den altså bli negativ etter at 3-3 er passert.
I stilling 5-5 har vi maksimal fluks igjen, men nå i motsatt retning av det vi hadde i stilling 1-1, altså -φ’. Når sløyfen har fullført en dreining på 360 o, har fluksen gjennom den variert som vist på Figur 7.
Vi skal se at fluksen som funksjon av vinkelen, α, kan skrives som: φ (α) = φ’ • cos(α). Av Figur 8 framgår at den delen av fluksen som flyter gjennom sløyfen er proporsjonal med det projiserte sløyfearealet vinkelrett på feltet. Projisert sløyfeareal ved en vilkårlig vinkel a ser vi kan skrives som:
\[A(\alpha) = l \cdot b \cdot cos(\alpha)\qquad{(4)}\]
Tilsvarende fluks gjennom sløyfen blir da:
\[\phi(\alpha) = B \cdot A(\alpha) = B \cdot l \cdot b \cdot cos(\alpha)\qquad{(5)}\]
Setter vi inn φ’=B • l • b, får vi altså
\[\phi(\alpha)= \phi' \cdot cos(\alpha)\qquad{(6)}\]
Dette er en cosinus-kurve og er tegnet ut på Figur 7. Vi ser av kurven at ved α = 0, dvs. i utgangsstillingen som vist på Figur 5, vil fluksen ikke forandre seg i det hele tatt pr. vinkelenhet hvis vi tenker oss en ørliten vinkeldreining fra dette punktet.
Da vil vi med andre ord ha dφ/dα=0 her. Det samme ser vi er tilfellet ved α=180 o, α=360 grader osv. for hver 180 o. Den største variasjonen pr. vinkelenhet ser at vi har ved α=90 grader og videre for hver 180 grader framover.
I disse punktene har derfor dφ/dα sine maksimalverdier. I Figur 7 er dφ/dα tegnet inn. Det kan vises at dφ/dα blir en sinuskurve som kan skrives:
\[d\phi/d\alpha = - \phi' \cdot sin(\alpha)\qquad{(7)}\]
Matematisk får en lign. Formel 7 direkte ved å derivere lign. Formel 6 med hensyn på vinkelen α.
Vi går nå tilbake til anordningen i Figur 5. Her tenker vi oss at sløyfen roterer med en konstant vinkelhastighet, ω, som angis i radianer pr. sek. Vi skal først se på hva vi mener med vinkelhastighet.
Vi vet at en i vinkeldreiing som tilsvarer en hel sirkelomdreining er det 2 π radianer.
Dersom vi tenker oss et turtall, n, på en omdreining pr. sek, vil altså den tilsvarende vinkelhastighet være 2 π radianer pr. sek. (r/s). Dersom turtallet angis i omdreininger pr.
minutt i stedet for pr. sek., vil altså et turtall på 60 omdreininger pr. minutt tilsvare en vinkelhastighet på 2π r/s. Generell sammenheng mellom turtall, n, og vinkelhastighet, ω, blir da:
\[\omega = 2\pi \cdot n/60\qquad{(8)}\]
Grunnen til at vi har innført vinkelhastigheten ω er at alle formler blir enklere da.
Når sløyfen Figur 5 roterer med konstant vinkelhastighet, ω, vil den i løpet av t sekunder ha dreid seg en vinkel som vil være proporsjonal med ω og t. Vi har med andre ord følgende sammenheng mellom vinkeldreining, vinkelhastighet og tid:
\[\alpha = \omega \cdot t\qquad{(9)}\]
Dersom vi nå går tilbake til uttrykket for fluks som funksjon av vinkelen, lign. Formel 6, og innfører lign. Formel 9, får vi fluksen som funksjon av tiden, noe som vi må ha for å kunne beregne indusert spenning. (Lign. Formel 2).
Vi får altså:
\[\phi (t) = \phi' \cdot cos(\omega \cdot t)\qquad{(10)}\]
For å finne indusert spenning må vi finne et uttrykk for hvordan fluksen varierer med tiden, dvs. dφ/dt. Siden lign. Formel 10 har samme form som lign. Formel 6, vil også dφ/dt ha samme form som dφ/dα slik vi kom fram til det i lign. eq:vannkraft_generator_generelt-om-vannkraftgeneratorer_generelle-prinsipper_eq-233. Imidlertid skjønner vi at desto fortere sløyfen roterer, desto større blir variasjonen i fluksen pr. tidsenhet. dφ/dt må derfor være proporsjonal med ω. Vi vil derfor få følgende uttrykk for dφ/dt:
\[d\phi/dt = -\omega \cdot \phi' \cdot sin(\omega \cdot t)\qquad{(11)}\]
Matematisk vil vi få dette resultatet direkte ved å derivere lign. Formel 10 med hensyn på tiden. Anvender vi nå induksjonsloven, lign. Formel 2 på dette og setter inn φ ’=B • b • l, får vi:
\[U(t) = -d\phi /dt = \omega \cdot B \cdot b \cdot l \cdot sin(\omega \cdot t)\qquad{(12)}\]
Dette er altså indusert spenning som funksjon av tiden i en sløyfe med areal b • l som roterer med en konstant vinkelhastighet, ω, i et homogent, magnetisk felt, B. Spenningen som induseres i sløyfen får en amplitudeverdi som er ω • B • b • l. Kaller vi den for U’, får vi:
\[U(t) = U' \cdot sin(\omega \cdot t)\qquad{(13)}\]
Denne funksjonen har vi tegnet inn på Figur 7.
Hvis vi tenker oss at vi måler denne spenningen med et voltmeter, så vil dette vise effektivverdien av spenningen. Effektivverdien for en sinusfunksjon fås ved å dividere amplitudeverdien med √2. Effektivverdien av spenningen blir:
\[U_{eff} = U'/\sqrt(2)\qquad{(14)}\]
eller hvis vi innfører U’=ω • B • b • l:
\[U = \omega \cdot B \cdot b \cdot l /\sqrt(2)\qquad{(15)}\]
Dersom vi bytter ut sløyfen med en spole som har N vindinger, ser vi at spenningen over spolen vil bli:
\[U = N \cdot \omega \cdot B \cdot b \cdot l/\sqrt(2)\qquad{(16)}\]
Lign. Formel 16 gir oss den fundamentale forståelsen av spennings- og induksjonsforholdene for en hvilken som helst elektrisk maskin.
Med ord kan vi summere det på følgende måte: Indusert spenning er proporsjonal med:
• antall vindinger i serie • omdreiningshastigheten (Turtallet) • feltstyrken i spolen (Magnetisering) • spolebredden (Poldeling) • spolelengen (Aksial jernlengde)
Vi skal senere se nærmere på praktiske anvendelser av disse prinsippene.
2.4 Magnetisk motstand og -potensial
Vi kjenner til at vi har en bestemt sammenheng mellom elektrisk potensial, strøm og resistans (Ohms lov) i en krets:
\[I = U/R\qquad{(17)}\]
Med ord kan vi si at strømmen, I, i en krets er proporsjonal med det drivende potensial, U, og omvendt proporsjonalt med resistansen, R, i kretsen.
En analog sammenheng har vi mellom magnetisk potensial, fluks og magnetisk motstand langs fluksveien i en magnetisk krets.
\[\phi = U_m/R_m\qquad{(18)}\]
Her representerer Um det drivende, magnetiske potensialet og kalles også den magnetomotoriske kraft (Analogt med Elektromotorisk kraft). Um er identisk med det drivende amperevindingstall, IN (Enhet = At, dvs ampereturn) som vi har over den magnetiske kretsen. Rm representerer den magnetiske motstanden langs fluksveien.
Vi skal være oppmerksomme på at Rm ikke alltid er en konstant, slik som en resistans er det. For jern vil den magnetiske motstanden være avhengig av feltstyrken. Jo større feltstyrken er, desto større blir den magnetiske motstanden. Dette kalles magnetisk metning. I uttrykket ovenfor vil Rm derfor også være en funksjon av φ . I det tilfellet får vi altså en ulineær sammenheng mellom fluks og magnetisk potensial.
For luft derimot, er det ingen metningsfenomener. Det betyr at den magnetiske motstanden for luft er konstant. Det kan vises at denne kan skrives:
\[R_{mo} = (1/\mu _o) \cdot\delta/A\qquad{(19)}\]
µo kalles permeabilitetskonstanten for luft og har størrelsen
\[\mu _o = 4 \cdot \pi \cdot 10^{-7} = 1.256 \cdot 10^{-6} [H/m]\qquad{(20)}\]
δ er luftgapets lengde i m.
A er luftgapets areal i m2.
Setter vi nå Formel 19 inn i Formel 18 og setter inn Um=IN får vi:
\[\phi = \mu _o \cdot IN \cdot A/\delta\qquad{(21)}\]
Innføres nå feltstyrken, B=φ/A, får vi
\[B = \mu _o \cdot IN/\delta\qquad{(22)}\]
Setter vi inn størrelsen på µo, ser vi at vi med litt avrunding får:
\[B = 1.256 \cdot 10^{-6} \cdot IN/\delta [T]\qquad{(23)}\]
Dette uttrykket gir oss altså muligheten til å beregne feltstyrken i et luftgap dersom vi kjenner de drivende amperevindingene over luftgapet og lengden på det.
For jern vil vi kunne gjøre samme resonnement. Her må vi da
innføre
permeabilitetskonstanten for jern. Denne oppgis gjerne som en
relativverdi i forhold til µo og betegnes gjerne
µr. Størrelsen på µr vil variere med
feltstyrken og den aktuelle størrelsen må tas ut fra en
permeabilitetskurve som gjelder for den jernkvaliteten vi har.
For jern får vi altså da:
\[B = \mu _r \cdot 1.256 \cdot (10^{-6}) \cdot IN/l_j [T]\qquad{(24)}\]
der lj er jernlengden i m.
2.5 Viserdiagrammer.
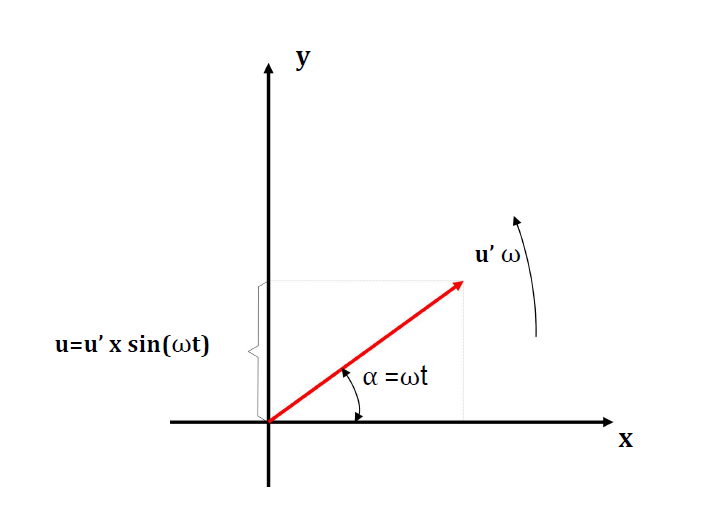
I stedet for å framstille tidsfunksjonene som f.eks. flukser og spenninger slik som vist i Figur 7, kan det i mange tilfeller være mer hensiktsmessig å betrakte funksjonene som vektorer eller visere som roterer med konstant vinkelhastighet, ω. Et slik framstilling kaller vi gjerne et viserdiagram.
På Figur 10 er vist et viserdiagram for spenningen, u, i Figur 9. Spenningen er her representert av en vektor (eller viser) som har en lengde lik spenningens amplitudeverdi, u’. Vi tenker oss at i utgangspunktet, ved tiden t=0, ligger spenningsvektoren langs den positive x-aksen. Etter en viss tid, t, har den rotert en vinkel α=ω • t. Dersom vi nå betrakter viserens projeksjon på y-aksen, ser vi denne får en lengde som er u • sin(ω • t), uansett i hvilken kvadrant viseren befinner seg. Vi legger også merke til fortegnet på viseren som er positiv i kvadrant 1 og 2, og negativ i kvadrant 3 og 4.
Projeksjonen på y-aksen er altså identisk med øyeblikks verdien av spenningen.
Vi legger spesielt merke til rotasjonsretningen. Den er pr. konvensjon alltid mot ur.
Den største fordelen med viserdiagrammet kommer best fram når
vi har flere vektorer, slik vi f.eks. hadde i Figur 7.
Her er det lett for å miste oversikten. I Figur 10
er de samme funksjonene framstilt i viserdiagram. Vi legger merke
til at det er visernes innbyrdes stilling som er av interesse.
Vinkelen mellom vektorene representerer
faseforskyvningen mellom dem. Denne er konstant, uavhengig av
tiden. Visernes stilling i forhold til en eller annen
referanseakse kan vi derfor velge vilkårlig.
3 Synkronmaskinens virkemåte
3.1 To-polet, enfase synkronmaskin.
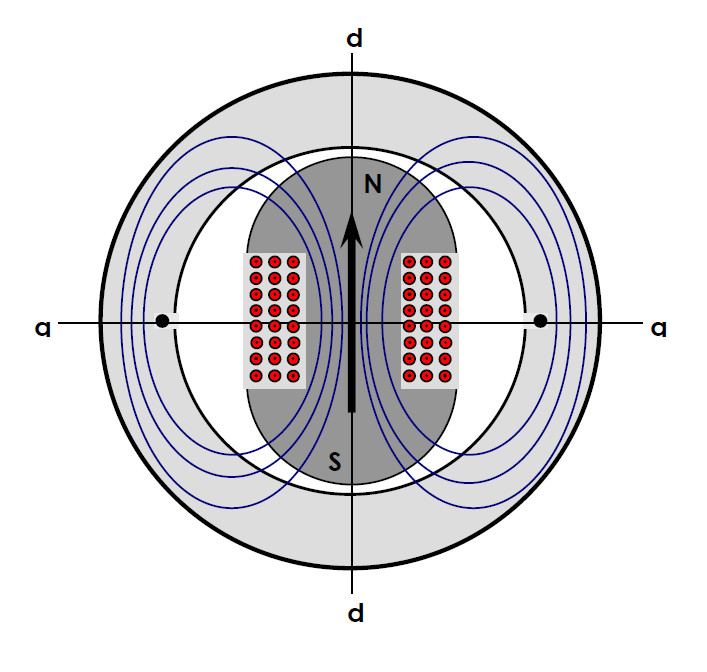
Figur 11 viser prinsippet for en 2- polet, 1- fase synkronmaskin. Magnetfeltet skaffes til veie av en roterende elektromagnet (Polhjul) med to poler. Polhjulet har en vikling som frembringer magnetfeltet og som vi kaller magnetiseringsvikling. (Feltvikling, polvikling og rotorvikling er også mye brukt). Uttakene for magnetiseringsviklingen kan vi f.eks. tenke oss er tilkoplet en ekstern spenningskilde (Magnetiseringsutstyr) via sleperinger.
Polhulet roterer med konstant hastighet inne i statoren som består av en jernring (Også kalt jernkjerne eller blikkpakke) og en statorvikling som i dette tilfellet består av en vinding montert i spor i jernkjernen.
Vi legger spesielt merke til utformingen av den ytterste delen av polene (Polskoformen). Denne er her utformet slik at vi oppnår en mest mulig sinusformet feltstyrke i luftgapet langs periferien av statorboringen. Vi ser at luftgapet er minst ved polenes senterlinje og øker på ut mot senterlinjen mellom polene (Pollukene).
Hvis vi går tilbake til lign. Formel 23 i Kapittel 2.4, ser vi at feltstyrken er omvendt proporsjonal med luftgapet. For å få til en sinusformet feltfordeling i luftgapet, må derfor den inverse verdien av dette, 1/ω, gjøres sinusformet.
Når polhjulet roterer, vil derfor fluksen gjennom
statorvindingen variere etter en
sinusfunksjon. Dette gir igjen en sinusformet spenning over
vindingen, slik som vi har sett i Kapittel 2.3.
Dersom polhjulet roterer med en konstant vinkelhastighet, ω • t,
kan vi tegne fluks og spenning slik som vist på Figur 12.
3.2 To-polet, trefase synkronmaskin.
På Figur 11 er vist en maskin med en vikling, dvs. en enfase maskin. Vi tenker oss nå at vi legger inn to viklinger til, og fordeler dem jevnt på omfanget. Viklingene blir da liggende med en vinkel 360/3 = 120 grader fra hverandre. Dette er vist på Figur 13.
Dersom polhjulet roterer med konstant vinkelhastighet, vil hver av viklingene få en indusert spenning nøyaktig som viklingen for enfasemaskinen, men spenningene vil være 120 grader faseforskjøvet i forhold til hverandre. Dette er vist på Figur 14.
Viklingene kan vi kople sammen, f.eks. til en stjernekopling som er det vanligste for generatorer. I dette tilfellet koples -a, -b og -c sammen til stjernepunkt og de andre endene vil da danne faseuttakene.
Vi har nå skaffet oss et trefase spenningssystem. Dette har vi tegnet i et viserdiagram i Figur 15 sammen med fluksen gjennom den enkelte spole. Vi legger merke til at spenningen for en fase er faseforskjøvet 90 grader etter fluksen i den tilsvarende vikling. Dette er i overensstemmelse med det vi har observert tidligere, f.eks. slik det framgår av Figur 10 og Figur 12.
3.3 Poltall - Turtall
Hvis vi ser på Figur 13 og tenker oss at polhjulet dreier seg en omdreining, så ser vi at spenningene har gjennomgått en periode. Det vil si at vektorene i viserdiagrammet, Figur 15 har dreid seg en omdreining, eller 360 grader.
Når vi betrakter vinkeldreininger for spenningsvektorer,
snakker vi om elektriske grader. En periode består altså av 360
elektriske grader. Vinkeldreining for polhjulet betegnes derimot
med mekaniske grader. For en 2- polet maskin, slik som vi har her,
ser vi at elektriske grader er det samme som mekaniske grader.
Hadde vi derimot hatt en maskin med fire poler, ville en periode,
360 elektriske grader, vært gjennomløpt i løpet av en halv
omdreining. For en 8- polet maskin ville en periode tilsvart en
kvart
omdreining, osv.
Det er altså en bestemt sammenheng mellom mekanisk og elektrisk vinkel og poltallet som vi kan skrive slik:
\[\omega _e = \omega _m \cdot p\qquad{(25)}\]
\[\phi e / t = \omega _m \cdot t \cdot p\qquad{(26)}\]
Divisjon med t gir:
\[\omega _e = \omega _m \cdot p\qquad{(27)}\]
ω_e : elektrisk vinkelhastighet ω_m : mekanisk vinkelhastighet p : antall polpar (halve poltallet)
Innfører vi her periodetallet, f, og turtallet, n, får vi:
\[\omega _e = 2\pi \cdot f\qquad{(28)}\]
\[\omega _m = \pi \cdot n/60\qquad{(29)}\]
Setter vi dette inn i lign. Formel 25 får vi:
\[2f = p \cdot n/60\qquad{(30)}\]
Sammenhengen mellom poltall, frekvens og turtall blir:
\[2p = 2f \cdot 60/n\qquad{(31)}\]
eller
\[n = 2f \cdot 60/2p\qquad{(32)}\]
For f=50 Hz får vi da følgende enkle sammenheng mellom poltall og turtall:
\[2p = 6000/n\qquad{(33)}\]
eller
\[n = 6000/2p\qquad{(34)}\]
Etter dette vil vi også skjønne at avstanden mellom to nordpoler (eller sydpoler) alltid, uavhengig av poltallet, vil være 360 elektriske grader. En poldeling, dvs. avstanden mellom to nabopoler, representerer altså alltid 180 elektriske grader.
3.4 Polskoformer. Grunnharmonisk felt.
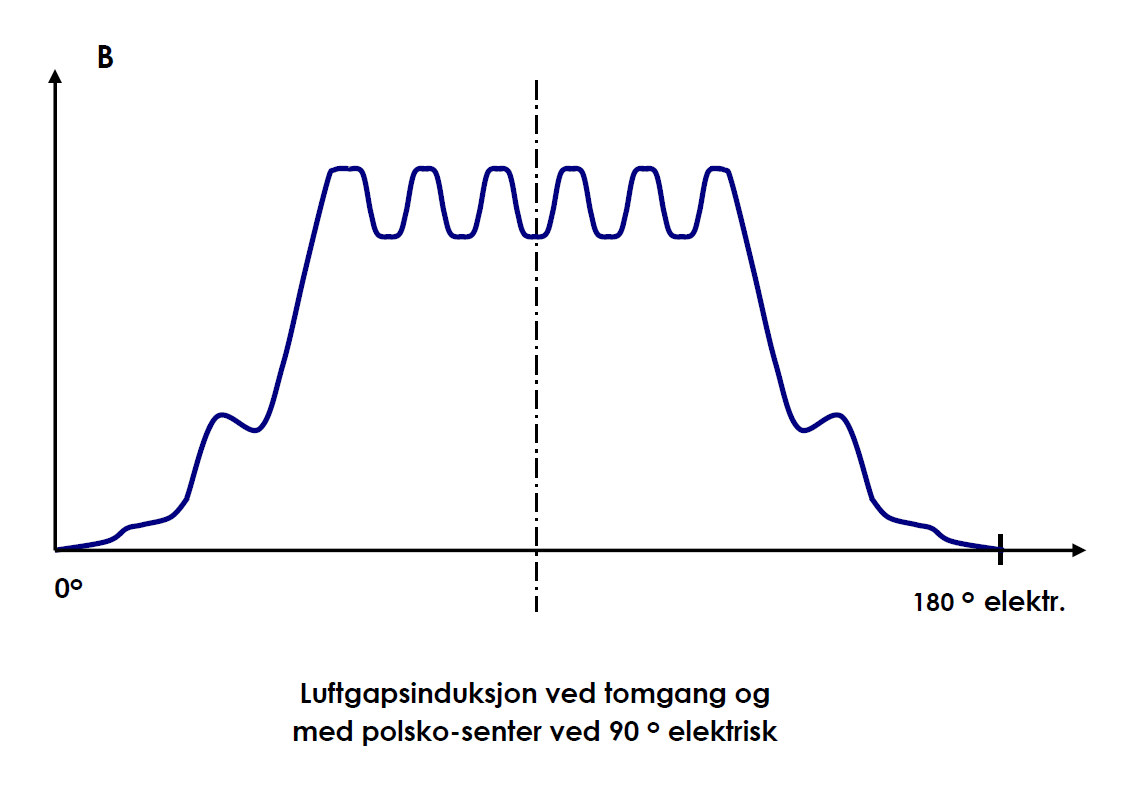
I eksemplene som er beskrevet i Kapittel 3.1 og Kapittel 3.2 forutsatte vi at polskoene ble utformet på en slik måte at feltfordelingen i luftgapet ble sinus-formet. I en praktisk maskin er ikke dette mulig å få til. Her vil de forskjellige maskinleverandører har sin egen måte å utforme polskoene på, men alle vil gi et luftgapsfelt som mer eller mindre avviker fra sinus-formen.
Det viser seg at enhver kurveform kan tenkes sammensatt av en rekke sinus-funksjoner med forskjellig frekvens. Vi har først en grunnharmonisk komponent. Denne har en bølgelengde på to poldelinger, slik som vi har det i de nevnte eksemplene. I tillegg har vi en rekke med overharmoniske komponenter med frekvenser som er et multiplum av grunnfrekvensen.
Det er bare den grunnharmoniske komponenten som vi er
interessert i da det er bare den som gir et nyttig bidrag til
generatorspenningen. De overharmoniske
komponentene skaper overtoner i spenningskurven og er derfor
uønsket. Virkningen kan begrenses ved forkortet viklingsskritt.
Dette blir beskrevet i neste avsnitt.
For å kunne beregne spenningen må vi altså kjenne størrelsen på den grunnharmoniske komponenten for feltkurven. For å gjøre det, kreves det en omfattende matematisk analyse som vi kaller Fourieranalyse. Denne analysen har vi gjort for de polskoformene som vi benytter. Hver type polskoform gir en bestemt feltkurveform som er den samme uansett dimensjoner og poltall.
I Figur 17 er vist en typisk feltkurveform. Amplituden for den grunnharmoniske feltkomponenten kaller vi B1. Den tilsvarende verdi for den virkelige feltkurven kaller vi Bδl.
Vi definerer nå forholdet mellom Bδ og Bδl som grunnharmonisk feltformfaktor og kaller den kB:
\[k_B = B_\delta/B_{\delta l}\qquad{(35)}\]
Hver type polskoform har altså sin bestemte kB som vi kjenner og kan bruke i beregningene.
3.5 Forkortet skritt. Skrittforkortningsfaktor.
I eksemplene foran har vi forutsatt en spole som strekker seg over over en poldeling, dvs. 180 elektriske grader. Dette gir maksimal spenning siden spolen da utnytter hele fluksen som flyter mellom polene.
Det er imidlertid vanlig å gjøre spoleskrittet noe kortere enn poldelingen. Dette gjøres for å redusere overharmoniske spenningskomponenter, spesielt av 5. og 7. harmoniske orden. Det kan vises at ved å velge spoleskrittet ca. 83 % av poldelingen, så får vi størst reduksjon av begge disse komponentene.
Spenningen blir altså som nevnt redusert ved forkortet spoleskritt. Reduksjonsfaktoren kalles skrittforkortningsfaktor og blir:
\[f_{sk} = sin((\tau _v/\tau _p) \cdot \pi/2)\qquad{(36)}\]
der τv er spoleskritt og τp er poldeling.
Skrittforkortningsfaktoren er altså forholdet mellom indusert spenning i en spole med forkortet skritt og indusert spenning i en spole med fullt skritt. Indusert spenning i en spole er nemlig, slik vi har sett det i Kapittel 2, proporsjonal med maksimal fluks gjennom spolen.
På Figur 19 er prinsippet med skrittforkortning antydet. Av figuren vil en kunne resonnere seg fram til uttrykket for skrittforkortningsfaktoren slik den er uttrykt i lign. Formel 36.
3.6 Fordelte viklinger. Viklingsfordelingsfaktor.
I de eksempler vi har studert har det alltid vært snakk om en spole pr. pol og fase. Dette er gjort for at det skulle være enkelt å beskrive prinsippene. I en praktisk maskin, derimot, må vi utnytte hele omfanget i statorboringen. Dette medfører at viklingene må fordeles jevnt utover statorboringen. Hver fase vil da få flere spoler under hver av polene. Hver fase vil få 180/3 = 60 elektriske grader pr. pol til disposisjon.
Disse spolene vil ligge i nabospor og vil derfor ha en avstand på en spordeling fra hverandre. Dermed vil vi få en viss faseforskjell i den induserte spenningen for hver av spolene. Fasevinkelen vil være identisk med vinkelen målt i elektriske grader mellom to nabospor (Sporvinkelen). Mellom ytterspolene vil vi ha 60 elektriske grader.
Spolene under en pol blir seriekoplet for hver fase. Siden spolespenningene ikke er i fase, vil spenningen for spolegruppen ikke bli eksakt lik summen av den enkelte spolespenning. Spenningene må nemlig summeres vektorielt, noe som gir en mindre spenning enn om alle spolene hadde samme fasevinkel. På Figur 20 er vist hvordan spenningene adderes for en vikling som har 3 spoler pr. pol og fase.
Reduksjonsfaktoren for spenningen på grunn av fordelte viklinger kaller vi viklings- fordelingsfaktor, fn. Denne vil i noen grad være avhengig av sportallet, men virkningen er liten. I praksis gjør vi liten feil om vi regner at fn er forholdet mellom 60 grader av sirkelbuen og den tilsvarende korde. Dette forholdet blir:
\[f_n = 3/\pi = 0.955\qquad{(37)}\]
3.7 Statorviklinger. Praktisk utforming.
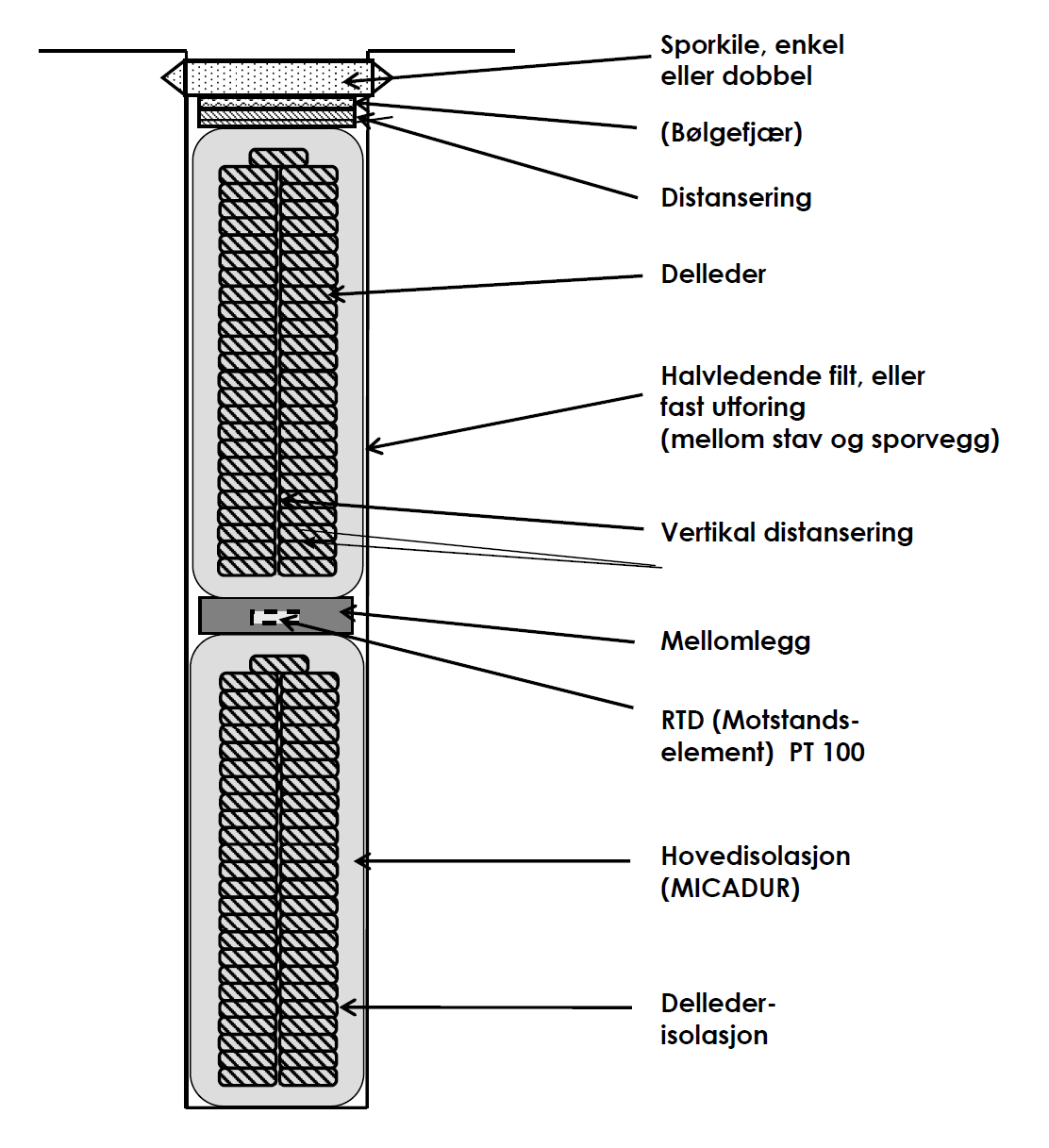
Statorviklingen er bygget opp av et visst antall staver som er lagt inn i spor i statorblikk- kjernen. Stavene kan bestå av en eller flere ledere. Ved en leder pr. stav snakker vi om envindingsspoler. Er stavene bygget opp av to eller flere ledere får vi det vi kaller flervindindsspoler. Se Figur 31 og Figur 32.
Viklingstyper
Stavene koples sammen etter forskjellige prinsipper til spoler og spolegrupper som igjen sammenkoples til den komplette vikling. Spesielt i eldre maskiner er ofte PLANVIKLINGER benyttet. Disse ligger med en stav i hvert spor. Sammenkoplingen mellom stavene må foregå i flere plan. Dette har gitt navn til denne typen viklinger. På Figur 21 er prinsippet for en slik vikling vist. En av ulempene med en slik vikling er at spolene blir forskjellige, alt etter hvilket lag de tilhører. Produksjonsmessig er ikke dette å foretrekke.
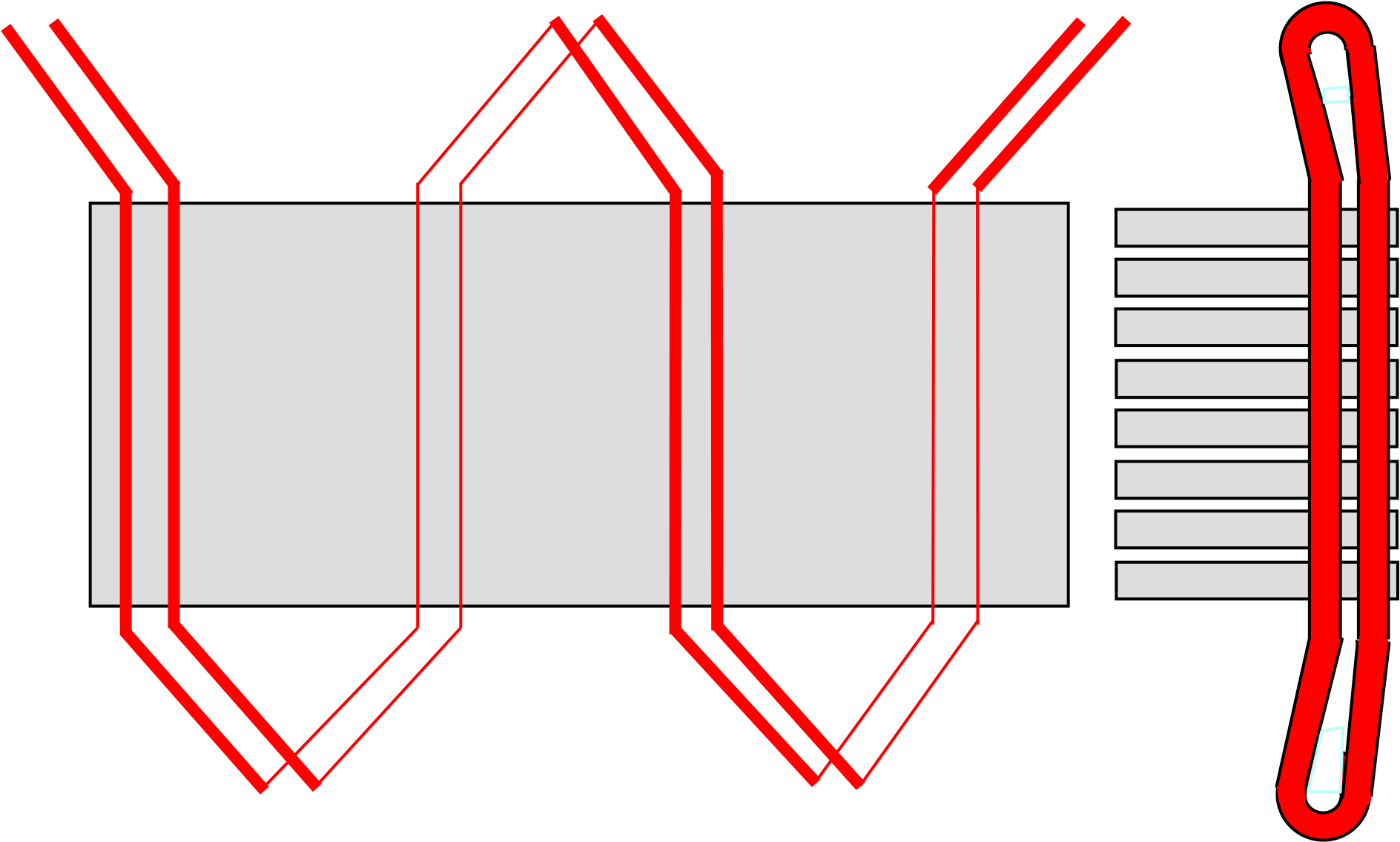
En annen type vikling er den såkalte BØLGEVIKLINGEN. Disse har to staver pr. spor, en bunnstav og en toppstav. Prinsippet for en bølgevikling er vist på Figur 22. Vi ser at viklingen går i en slags bølge langs omfanget av stator, derav navnet.
Sammenkoplingen mellom stavene går fra bunnstav til toppstav og kan foretas i ett plan i motsetning til planviklingen.
En tredje type vikling er SLØYFEVIKLINGEN som er lik bølgeviklingen bortsett fra at sammenkoplingen mellom stavene er slik at det dannes sløyfer for hver pol. Prinsippet for en sløyfevikling er vist på Figur 23.
Hvirvelstrømtap
Hver leder er (som regel) bygget opp av et visst antall delledere. Disse er parallellkoplet på visse punkter i viklingen alt etter hvilken viklingstype vi har.
Oppdelingen i delledere er gjort for å redusere tap i viklingen
på grunn av strømfortrengning i lederen. Denne oppstår fordi det
mellom tennene i statorkjernen (på tvers av sporet, og altså
gjennom lederen) vil flyte en magnetisk fluks (lekkfluks) som blir
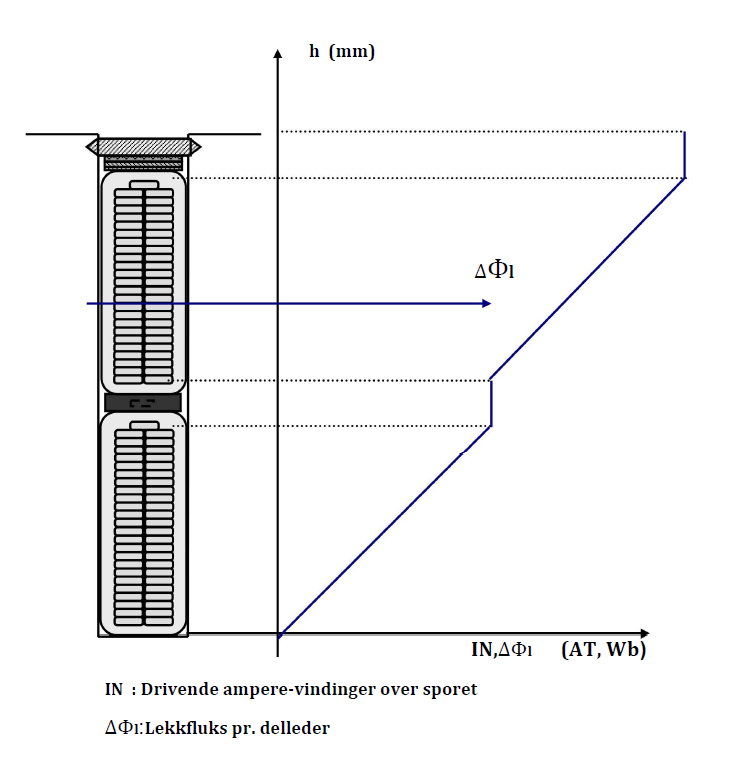
drevet av strømmen i lederen. På Figur 25
er vist hvordan de drivende
amperevindinger for lekkfluksen varierer over sporhøyden.
En massiv leder ville kunne få meget store hvirvelstrømtap på grunn av dette fenomenet. Jo flere delledere vi velger, desto mindre blir hvirvelstrømtapene. Dette er fordi delledertykkelsen har blitt mindre. I praksis settes en øvre grense for tillatt hvirvelstrømtap, og dermed er også minste antall delledere gitt.
Sirkulasjonstap
Lekkfluksen mellom tennene varierer over sporhøyden. I bunnen av sporet er den null og er størst i toppen. Dette betyr at den øverste dellederen blir gjennomflytt av en større lekkfluks enn de underliggende. Den induserte spenningen som den enkelte delleder får på grunn av lekkfluksen, blir dermed størst for de øverste dellederne.
Dersom vi tenker oss at vi parallellkoplet dellederne i hver
ende av stavene, ville den spenningsdifferanse som vi har mellom
de forskjellige dellederne drive en
sirkulasjonsstrøm mellom dellederne. Dette ville føre til
tilsvarende sirkulasjonstap som vil kunne bli av vesentlig
størrelse.
Transponering
For å redusere sirkulasjonstapene blir dellederne transponert etter forskjellige systemer.
Prinsippet med alle typer transponeringer er at vi sørger for at spenningsdifferansen mellom dellederne blir helt eller delvis eliminert mellom de punktene der dellederne skal parallellkoples.
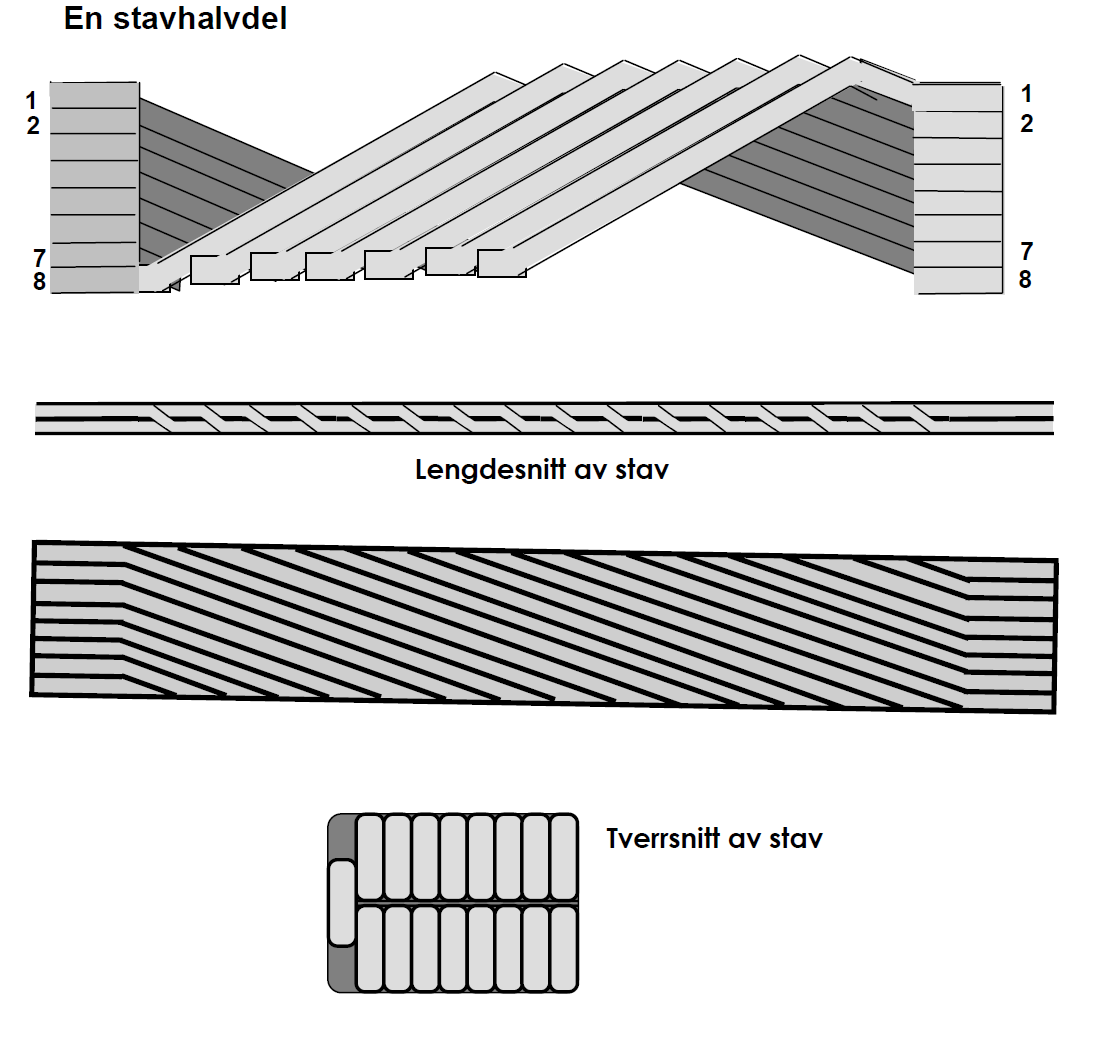
Dersom parallellkoplingen foretas i hver ende av hver stav, eller i hver spoleende, må transponeringen gjøres i sporet. Den vanligste metoden her er kalt ROEBEL- metoden. I Figur 27 framgår prinsippet for en Roebelvikling. Figuren viser den ene halvparten av en Roebelstav. Den andre halvparten har motsvarende form, slik at begge halvpartene til sammen gir en rektangulær form som vist nederst på figuren.
Ved denne metoden vil hver delleder innta samtlige posisjoner over sporhøyden en eller flere ganger. Dermed har vi oppnådd at hver delleder i gjennomsnitt over stavlengden har blitt utsatt for like mye lekkfluks. Dermed er også den induserte spenningen lik for alle dellederne og sirkulasjonsstrømmene blir dermed eliminert.
En annen måte å løse problemet med sirkulerende strømmer på er å føre dellederne isolert fra hverandre gjennom hele viklingen fra faseuttak til nullpunkt. Da kan transponeringen foretas i koplingen mellom de forskjellige stavene eller spolegruppene på en slik måte at spennings-differansen for et visst antall staver blir mest mulig nøytralisert av resten av stavene.
Viklingsskjema
For å forklare viklingsskjemaet, har vi valgt å studere en 4-polet trefasemaskin. Prinsippet for denne er vist på Figur 28. Viklingen er en 2- lags, 3- fase, symmetrisk sløyfevikling. Viklingen er lagt ut med et totalt sportall på Q=30. Iflg. lign. Formel 25 blir elektrisk vinkel rundt hele omkretsen på maskinen:
\[\omega _e = 360 \cdot 4/2 = 720^{\circ}\qquad{(38)}\]
Elektrisk vinkel mellom to nabospor blir ωe/Q = 720/30 = 24 grader.
Spenningen i den vindingen som har overstav i spor 2 ligger 24 grader etter spenningen i vindingen som har overstav i spor 1. Mekanisk sporvinkel er 12 grader. Antall spor pr. pol blir:
\[Q/(2p) = 30/4 = 7,5 spor\qquad{(39)}\]
Dette er ikke noe annet enn poldelingen uttrykt i antall spor. Med et relativt spoleskritt på 0,83 gir dette ett spoleskritt på 7,50,83 = 6,2 spor.
Spoleskrittet må selvsagt være et helt tall. Vi velger spoleskritt = 6 spor. Relativt spoleskritt blir da 6/7,5 = 0.8. Iflg. lign. Formel 36 gir dette en skritt- forkortningsfaktor på
\[f_{sk} = sin(0,8 \cdot 90^{\circ}) = sin 72^{\circ} = 0,951\qquad{(40)}\]
Antall spor pr. pol og fase blir:
\[q = Q/(2p\cdot 3) = 30/(4\cdot 3) = 2 1/2\qquad{(41)}\]
Vi kan selvfølgelig ikke ha halve vindinger. For å få til q=2 1/2 må vi gjøre det slik at vi i gjennomsnitt over en strømkrets i en fase får dette. I dette tilfellet oppnår vi det ved å legge 3 vindinger under annenhver pol, og 2 under den andre halvparten av polene.
Vinding 1 ligger med overstav i spor 1 og får understav i spor 7. På Figur 28 er disse merket med a1. På fig. er også resten av viklingen inntegnet.
For å bestemme hvilken fase en vinding skal tilhøre, deles stator inn i 2p • 3 = 12 soner som hver er på 60 elektriske grader, slik som vist på Figur 29. De vindingene som har overstav i den første sonen, legges til fase A. De som har overstav i den andre sonen legges til fase C, men med negativt fortegn i forhold til A- fasen. De som har overstav i sone 3 legges til fase B, med positivt fortegn. Forholdene framgår av Tabell 1 :
| Sone | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Fase | A | -C | B | -A | C | -B | A | -C | B | -A | C | -B |
| Elektrisk vinkel | 0- 60 | 60- 120 | 120- 180 | 180 - 240 | 240 - 300 | 300 - 360 | 0- 60 | 60- 120 | 120 - 180 | 180 - 240 | 240 - 300 | 300- 360 |
| El.vinkel + kopl.vinkel | 0- 60 | 240- 300 | 120- 180 | 0- 60 | 240 - 300 | 120 - 180 | 0- 60 | 240 - 300 | 120 - 180 | 0- 60 | 240 - 300 | 120- 180 |
Tabell 1 viser at de vindingene som er koplet til fase A har elektrisk vinkel mellom 0 og 60 grader, de vindingene som er koplet til fase B har elektrisk vinkel mellom 120 og 180 grader, og de vindingene som er koplet til fase C har elektrisk vinkel mellom 240 og 300 grader. Det er da tatt hensyn til at noen vindinger er koplet med negativt fortegn.
Hvis en beregner resultanten av spenningsvektorene innenfor hver sone vil en finne at de ligger faseforskjøvet 120 grader i forhold til hverandre og danner et symmetrisk trefase-system.
Figur 30 viser koplingen av vindingene i fase A. Et slikt skjema kalles gjerne vikleskjema. Et komplett vikleskjema omfatter alle tre fasene og ikke som her bare den ene. Uttaket merket A er faseuttak, mens uttaket merket Ao er nullpunkt. Overstaver er tegnet med heltrukket linje, understaver er stiplet.
Strømretningen i overstavene er inntegnet. Det framgår at sammenkoplingen av viklingen av vindingene er gjort slik at vindinger som skal koples med negativt fortegn har piler som peker nedover på papiret. De som skal koples med positivt fortegn har piler som peker oppover.
3.8 Beregning av klemmespenning.
Vi skal nå finne et uttrykk for klemmespenningen for en vilkårlig maskin. Vi definerer først noen symboler som vi har bruk for i beregningen.
| Beskrivelse | Symbol | Enhet |
|---|---|---|
| Innerdimeter | D | [m] |
| Brutto lengde | L | [m] |
| Poldeling | τp | [m] |
| Klemmespenning | U | [kV] |
| Sportall | Q | [-] |
| Spor pr. pol og fase | q | [-] |
| Antall ledere pr. spol | Ns | [-] |
| Antall parallelle strømkretser pr. fase | c | [-] |
| Skrittforkortningsfaktor | fsk | [-] |
| Viklings- fordelingsfaktor | fn | [-] |
Spenning i en vinding med fullt skritt
For å komme videre trenger vi et uttrykk for spenningen pr. vinding. Figur 33 viser grunnhamoninsk felt under en pol. For å få den tilhørende fluksen, må vi integrere feltstyrken over en poldeling. Det viser seg at denne blir:
\[\phi ' = (2/\pi) \cdot B_1 \cdot \tau _p \cdot L\qquad{(42)}\]
Innfører vi nå τp=π • D/(2p), får vi:
\[Q' = B_1 \cdot D \cdot L/p\qquad{(43)}\]
For å finne spenningen, trenger vi fluksen som funksjon av tiden:
\[\phi (t) = \phi ' \cdot cos(\omega \cdot t)\qquad{(44)}\]
som gir:
\[\phi (t) = (B_1 \cdot D \cdot L/p) \cdot cos(\omega \cdot t)\qquad{(45)}\]
Spenningen i vindingen som funksjon av tiden blir dermed:
\[u(t) = -d\phi/dt = (\omega \cdot B_1 \cdot D \cdot L/p) \cdot sin(\omega \cdot t)\qquad{(46)}\]
Effektivverdien av spenningen fås ved å dividere amplitudeverdien med √2:
\[u_e= \omega \cdot B_1 \cdot D \cdot L/(p \cdot \sqrt(2))\qquad{(47)}\]
Klemmespenning
Spenningen i en vinding med forkortet skritt får vi ved å multiplisere uttrykket i lign. Formel 47 med skrittforkortningsfaktoren, fsk:
\[u_v = f_{sk} \cdot \omega \cdot B_1 \cdot D \cdot L/ (p \cdot \sqrt(2))\qquad{(48)}\]
La oss nå si at viklingen er utført med nf vindinger i serie pr. fase. For en 2- lagsvikling gi dette:
\[n_f= (Q/3) \cdot (n_s /2)/c\qquad{(49)}\]
Dette gir en fasespenning for viklingen:
\[Uf = u_v \cdot n_f \cdot f_n\qquad{(50)}\]
som innsatt gir:
\[U_f = f_n \cdot f_{sk} \cdot \omega \cdot B_1 \cdot D \cdot L/ (p \cdot \sqrt(2))\qquad{(51)}\]
\[U_f = \omega \cdot B_1 \cdot D \cdot L \cdot q \cdot (n_s/c) \cdot f_{sk} \cdot f_n /\sqrt(2)\qquad{(52)}\]
Klemmespenningen på maskinen fås ved å multiplisere Uf med √3. Dersom vi gjør det og samtidig setter inn ω=2π • f, får vi:
\[U = 0.385 \cdot B_1 \cdot D \cdot L \cdot q \cdot (n_s/c) \cdot f_{sk} \cdot f_n \cdot (f/50)\qquad{(53)}\]
Dette er altså det generelle uttrykket for klemmespenningen i en vilkårlig synkronmaskin.
Utlegging av statorvikling
Når vi skal konstruere en vikling for en maskin gjelder det å finne et et sportall som er gunstigst ut fra de aktuelle maskindata. Dessuten må en bestemme viklingens oppdeling i antall ledere pr. spor, ns, og antall parallelle strømkretser pr. fase, c. Alle disse verdiene er gitt implisitt i lign. Formel 53. Løser vi ligningen med hensyn på disse størrelsene, får vi:
\[q \cdot (n_s/c) = 2.6 \cdot (50/f) \cdot U/(B_1 \cdot D \cdot L \cdot f_{sk} \cdot f_n)\qquad{(54)}\]
Alle størrelser som inngår i dette uttrykket er kjente innenfor nokså snevre grenser. Vi kjenner frekvensen, f. Spenningen, U, er enten gitt fra kunden eller vi kan velge en gunstig verdi selv. Fordelingsfaktoren, fn, kan settes til 0.955, slik som vi så i lign. Formel 37. Skritt-forkortningsfaktoren, fsk, vil ligge rundt 0.96. Denne verdien må vi justere etter at det endelige sportallet er bestemt.
Feltstyrken B1 blir valgt i området 0.7 - 1.0 Tesla alt etter maskintype.
Diameteren D og lengden L er bestemt ut fra krav til svingmoment, rusningsturtall og hvor høy utnyttingsgrad vi velger for maskinen. Denne er igjen bestemt av krav til temperaturer, reaktanser og virkningsgrad. Vi skal se litt på dette i neste kapittel.
4 Generelle utleggingsprinsipper
4.1 Utnyttelse.
Når vi skal bestemme maskinens hoveddimensjoner, dvs. diameter (D) og lengde (L) tar vi utgangspunkt i maskinens utnyttelsesfaktor (C). Denne er definert slik:
\[C = S/(D^2 \cdot L \cdot n)\qquad{(55)}\]
der S er maskinens ytelse (kVA), D er boringsdiameter (m), L er jernfeltets lengde (m) og n er maskinens nominelle turtall (o/min).
Vi ser at utnyttelsesfaktoren er proporsjonal med ytelsen pr. volumenhet for boringen, (Boringsvolum: (π /4) • D2 • L), og er derfor et mål på hvor mye ytelse en har lagt inn i dette volumet ved det aktuelle turtallet. Høy utnyttelsesfaktor betyr at materialene er i maskinen er høyt utnyttet, både elektrisk, magnetisk og mekanisk.
Generelt kan vi si at jo høyere utnyttelsesfaktor, jo vanskeligere blir det å bli kvitt tapsvarmen og jo vanskeligere blir det å oppnå lave reaktanser. I tillegg blir det også vanskeligere å oppnå tilstrekkelig svingmasse for maskinen.
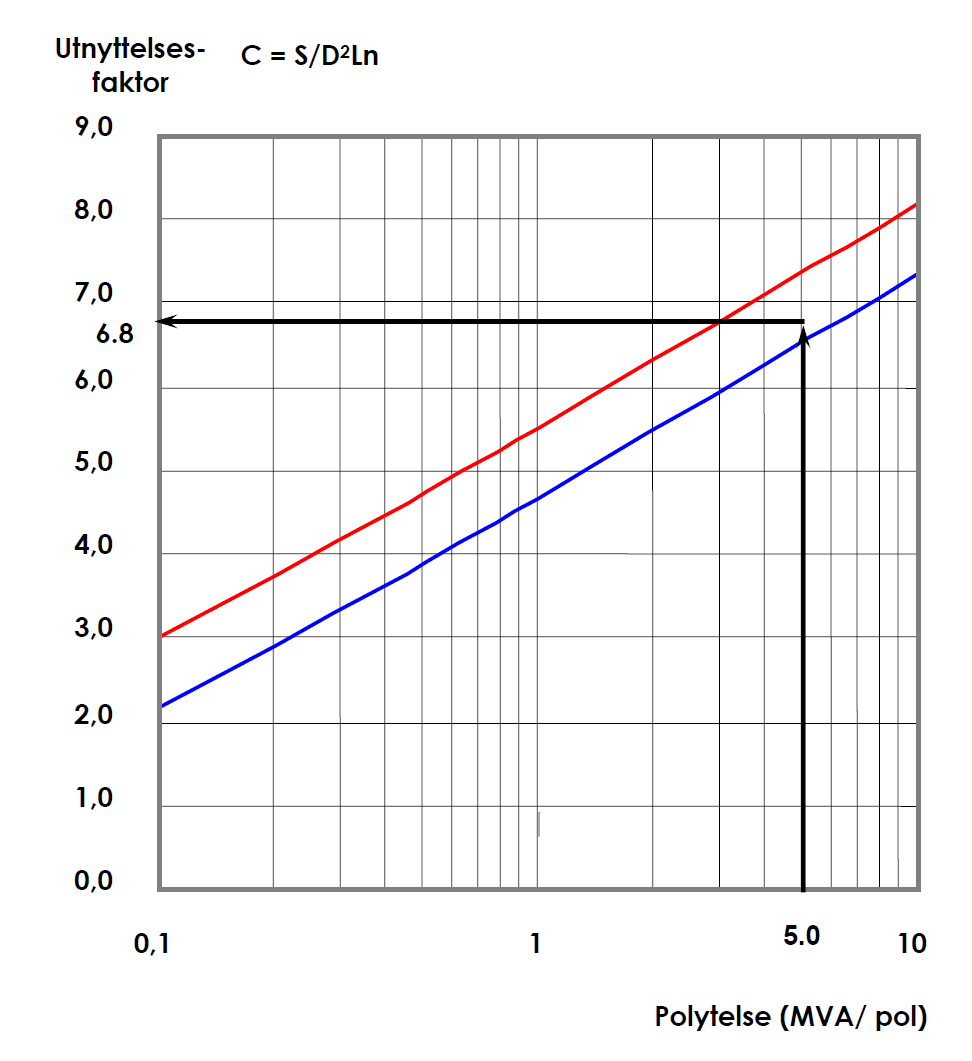
I praksis har hvert firma sine erfaringskurver for utnyttelsesfaktoren for de forskjellige turtall, ytelsesområder og maskintyper. Som regel vil en ha kurver der utnyttelsesfaktoren er gitt som funksjon av ytelse pr. pol. (Se Figur 34). Dermed kan en si at utnyttelsesfaktoren er kjent på utleggingstidspunktet og denne vil bli brukt som et utgangspunkt for den videre beregning.
Med utgangspunkt i lign. Formel 55 får vi:
\[D^2 \cdot L = S/(C \cdot n)\qquad{(56)}\]
4.2 Svingmasse.
Svingmassen, Θ, for en rotor er difinert som:
\[\theta = G \cdot D_{t}^2\qquad{(57)}\]
der G er rotorvekten (tonn) og D_t er rotorens tyngdepunktsdiameter (m). Svingmassen er som regel bestemt av turbinleverandøren ut fra stabilitetshensyn og turtallsstigning ved lastavslag.
Siden G er proporsjonal med rotorvolumet og D_t er proporsjonal med boringsdiameteren, får vi:
\[\theta = \beta \cdot D^4 \cdot L\qquad{(58)}\]
eller
\[D^4 \cdot L = \theta /\beta\qquad{(59)}\]
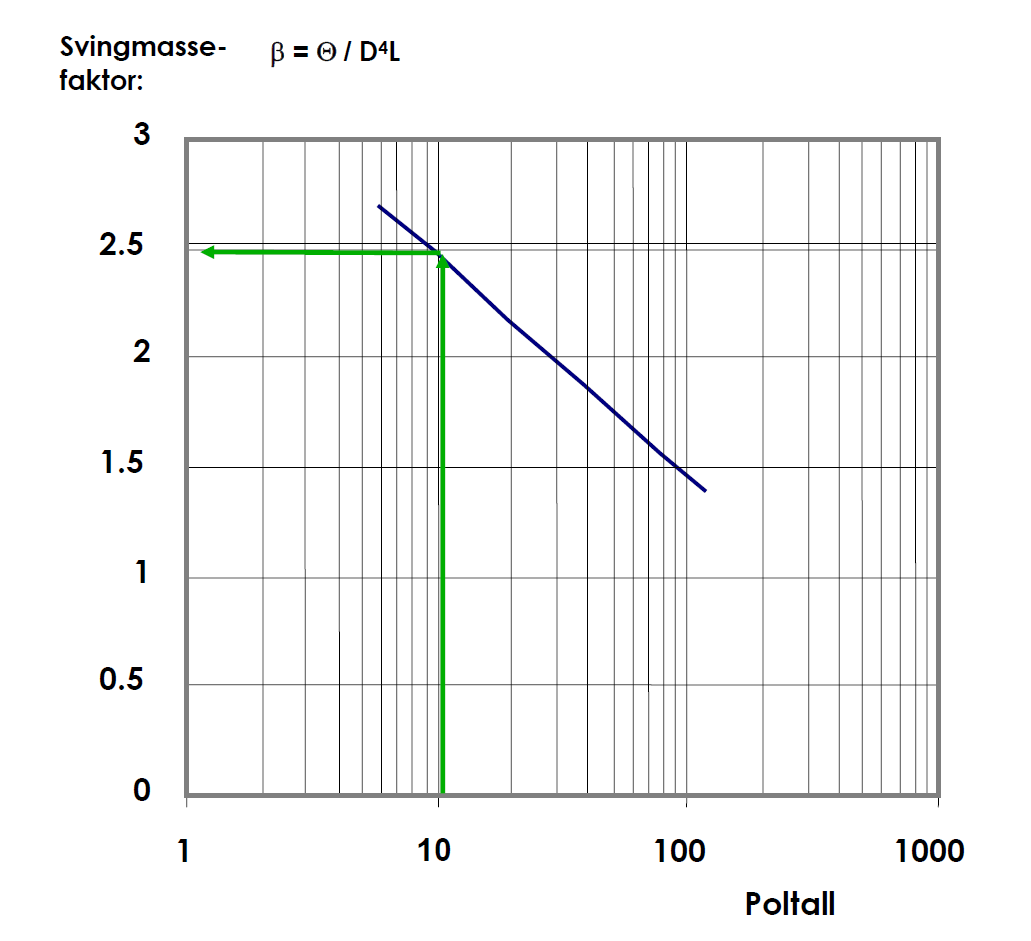
Proporsjonalitetsfaktoren β er en erfaringsverdi for de forskjellige poltall og finnes gjerne i kurveform. (Se Figur 34)
4.3 Bestemmelse av hoveddimensjoner.
Matematisk ser vi at lign. Formel 56 og Formel 59 utgjør et ligningssett med to ligninger og to ukjente og dermed er både D og L bestemt:
\[D = \sqrt( (\theta \cdot C \cdot n)/(\beta \cdot S) )\qquad{(60)}\]
\[L = S / ( C \cdot n D^2)\qquad{(61)}\]
Verbalt kan vi si at diameter og lengde på maskinen må velges slik at kravet til svingmasse er oppfylt samtidig som utnyttelsen må være mest mulig optimal med hensyn til balansen mellom vekt (pris), temperaturer, reaktanser og tap.
4.4 Eksempel.
Vi skal finne passende diameter og lengde for en generator som er levert:
| Ytelse: | S = 50000 | kVA |
| Svingmasse: Nom. | Θ = 260 | tm2 |
| Turtall: Rusn. | n = 600 | o/min |
| Turtall | nr= 1100 | o/min |
Vi finner først poltallet etter lign. Formel 33: 2p = 6000/n = 6000/600 = 10.
Så regner vi ut ytelsen pr. pol: S/2p = 50/10 = 5 MVA/pol.
Dermed kan vi finne utnyttelsesfaktoren C = 6.8 av Figur 34 (ca. midt i området) og svingmassefaktoren Θ = 2.5 av Figur 35. Diameter og lengde fås dermed av lign. Formel 60, hhv. Formel 61 :
\[D = \sqrt((260 \cdot 6.8 \cdot 600)/(2.5 \cdot 50000)) = 2.92 ( m )\qquad{(62)}\]
\[L = 50000/(6.8 \cdot 600 \cdot 2.92^2) = 1.69 (m)\qquad{(63)}\]
Denne maskinen ble opprinnelig lagt ut med D = 2.6 m og L = 2.0 m. Utnyttelsesfaktor C = 6.16.
Grunnen til den slanke utførelsen var hensynet til mekaniske påkjenninger ved rusning. En måte å få et inntrykk av dette på er å se på periferihastigheten for rotorens ytterflate ved rusning.
Ved D = 2.92 m blir den 168 m/sek. og ved 2.6 m: 150 m/sek. Erfaringen tilsier at kommer vi over 150 m/sek, begynner påkjenningene å bli så store at vi må ty til forholdsvis dyre løsninger. (Dyrere materialkvaliteter, Større polklør, tykkere rotorring etc.)
Når det gjelder utleggelsen av diameter og lengde, er det også en rekke andre hensyn en må ta i betraktning slik som transportdimensjoner (seksjonsoppdeling), montasjeforhold, bygningsmessig tilpassing, kritisk turtall, etc.
Når det gjelder utnyttelsesfaktoren kan det ha vært hensynet til tap og reaktanser som har gjort at en ikke har ønsket å gå høyere enn 6.16.
5 Typiske byggeformer
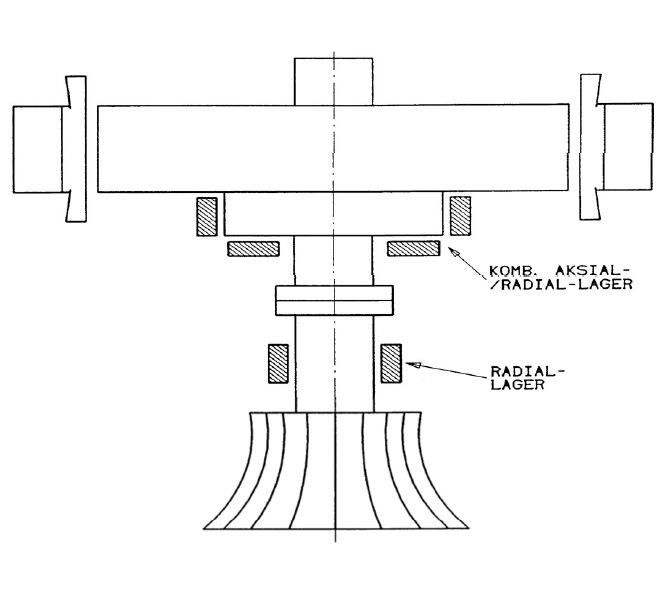
Med bygeform mener vi ofte hvordan lagrene er plassert i forhold til generatorens rotor. I Figur 36 er det vist noen eksempler på dette. For vertikale aggregater kan vi skille mellom to hovedgrupper:
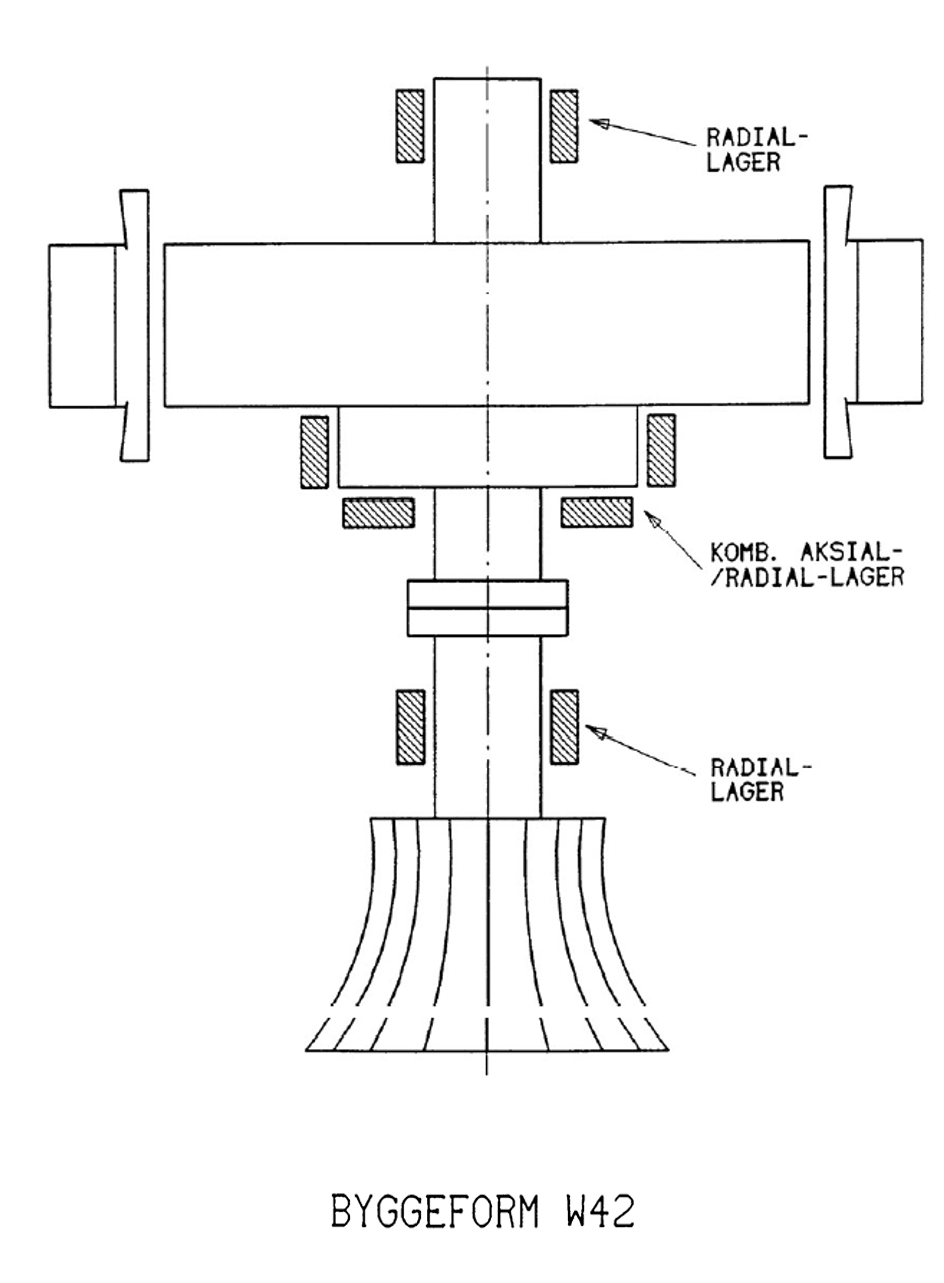
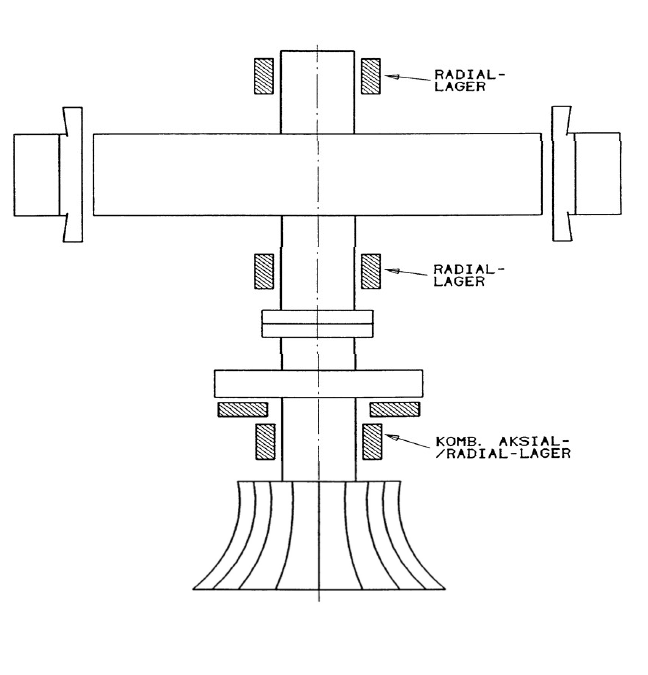
Bærelageret plassert under rotor (Se W42, W3, W8 og W6)
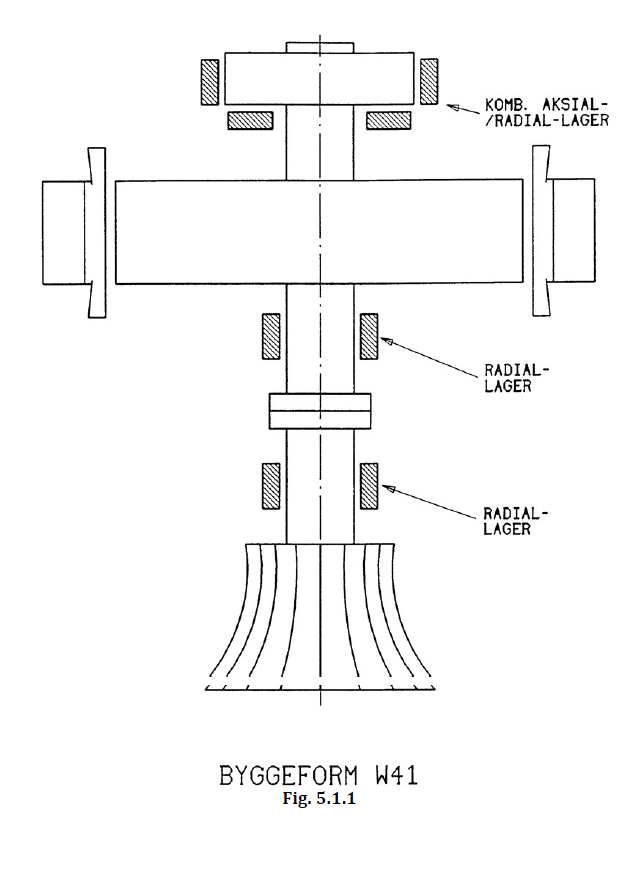
Bærelageret plassert over rotor (Se W41)
Generelt kan vi vel si at langsomtløpende maskiner ofte får bærelageret plassert under rotor, mens de fleste hurtigløpende har overliggende bærelager. Vi skal se litt nærmere på hver av disse kategoriene.
5.1 Langsomtløpende generatorer.
Langsomtløpende generatorer har forholdsvis stor statordiameter med tung rotor og stor hydraulisk tilleggslast fra turbinen. Turbinsjaktens diameter er som regel mindre enn statorboringens diameter. Med lageret plassert under rotoren vil en derfor få et enklere og lettere armkryss og overføringen av kreftene fra lageret via armkrysset til fundamentet blir også enklere. Et eksempel på dette er vist i Figur 42. som har et lagerarrangement tilsvarende W42 i Figur 37.
Som det framgår av figurene i figurene (Figur 36 - Figur 40) finnes det flere alternative lagerarrangement under hovedgruppe 1. Byggeformene W8 og W6 er begge det en kaller for “paraplymaskiner”, dvs. de har intet styrelager over rotor. Dette gir en enklere og billigere løsning og en sparer tap i ett styrelager.
Spørsmålet om en kan sløyfe øvre styrelager er imidlertid avhengig av hvor høyt kritisk turtall en kan oppnå med denne løsningen. Et vanlig krav er at kritisk turtall skal ligge 15 til 20 % over rusningsturtallet for aggregatet.
For langsomtløpende maskiner vil de mekaniske deformasjonene i rotor være den begrensende faktor på grunn av de store dimensjonene, mens de mekaniske spenningene som regel er relativt lave. Rotorringen består ofte av blikksegmenter som vanligvis bygges opp på anlegg på grunn av transportbegrensningene. Dette kalles ofte “kjederotor” fordi segmentene lenkes sammen med bolter til et slags ringkjede.
Kjederotorer blir ofte utført som såkalt “ventilert ring”, dvs. utført med radielle ventilasjonskanaler som gir en meget jevn ventilasjonen og dermed kjøling av både feltvikling og stator. Dette systemet er også gunstig på grunn av at en ikke behøver de påbygde viftene.
5.2 Hurtigløpende generatorer
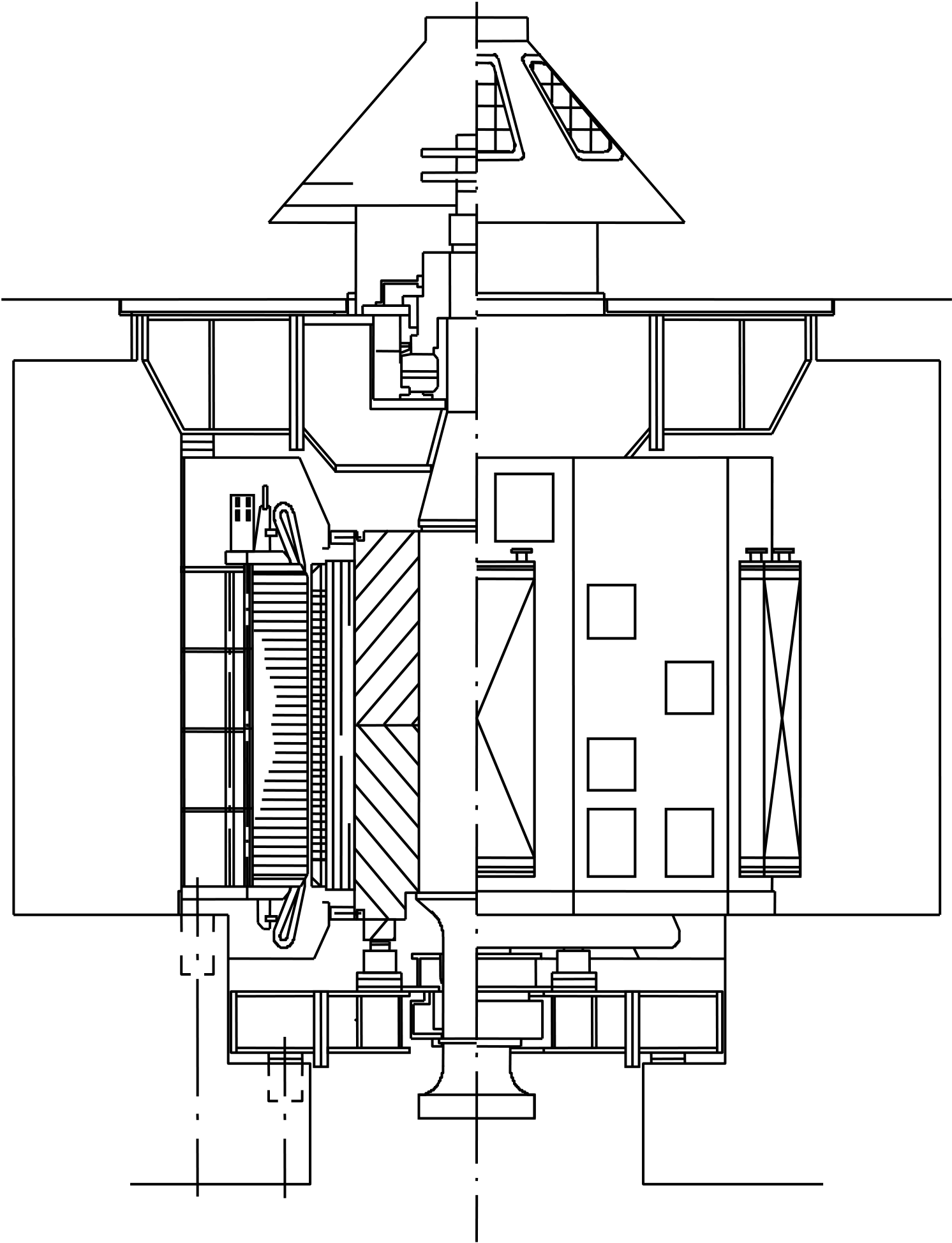
Hurtigløpende generatorer utføres vanligvis med et kombinert bære-/ styrelager plassert over rotoren. Denne typen maskiner har som regel relativt stor jernlengde i forhold til diameteren, og blir derfor oftest utført med et underliggende styrelager i tillegg på grunn av kravet til kritisk turtall. Et typisk eksempel på en slik utførelse er vist på Figur 41 som har et lagerarrangement tilsvarende W41 i Figur 36.
For hurtigløpende maskiner er det de mekaniske spenningene i rotor som er begrensningen på grunn av det høye rusningsturtallet. De mekaniske deformasjonene er som regel aldri noe problem. I tillegg vil kritisk turtall ofte begrense konstruksjonsmulighetene på grunn av den slanke utførelsen med en forholdsvis lang akselstreng, i kombinasjon med høyt rusningsturtall.
Rotorringen blir ofte utført i smidd stål som er krympet på et nav. Noen ganger er det ikke plass til navet fordi påkjenningene i ringen krever så tykk ring. I slike tilfeller blir rringen krympet direkte på akselen. I ekstreme tilfeller vil heller ikke dette være nok og en må smi aksel og rotorring i ett stykke. Dette henger også sammen med kravet til kritisk turtall.
For hurtigløpende maskiner blir ventilasjonen vanligvis besørget av aksielle vifter med justerbare bladvinkler, en vifte på hver ende av rotor.
5.3 “Størrelse” og “teknologi”
Vi har tatt med disse begrepene for å illustrere forskjellen i de tekniske utfordringer som vi møter for typisk langsomtløpende og for hurtigløpende maskiner. Definisjonene er som følger:
Størrelse: Generatorytelse dividert på turtallet, dvs.:
\[Størrelse = S/n (MVA/opm)\qquad{(64)}\]
Teknologi: Generatorytelse multiplisert med turtallet, dvs.:
\[Teknologi = S \cdot n/1000 (MVA/opm/1000)\qquad{(65)}\]
Dersom vi kombinerer uttrykket Formel 64 med uttrykket Formel 55 i forrige kapittel vil vi få:
\[Størrelse = C \cdot D^2 \cdot L = k \cdot C \cdot V (MVA/opm)\qquad{(66)}\]
der k er en proporsjonalfaktor og V er volumet av generatorboringen.
Dersom vi i Formel 65 setter inn n = 6000/2p (Gjelder for 50 hz), får vi
\[Teknologi = 6 \cdot (S/2p) (MVA/pol)\qquad{(67)}\]
Det finnes et eksempel i Tabell 6.
“Størrelsen” er altså proporsjonal med volumet av statorboringen og derfor et begrep om de fysiske dimensjoner for generatoren. Her er utfordringen spesielt å mestre de makaniske deformasjonene, feks når det gjelder rundhet.
“Teknologien” er proporsjonal med ytelsen pr pol, noe som vi ofte betegner “polytelse”. Denne er altså et uttrykk for hvor mye generatorytelse som faller på hver pol. Det viser seg at jo større dette tallet er, jo vanskeligere teknisk blir det å mestre konstruksjonen, feks. kjølemessig og mekanisk. Derav kommer navnet “Teknologi”.
Ut fra dette forstår vi at for langsomtløpende maskiner (lavt turtall, stort volum) så vil vi finne at “størrelsen” er høy. For hurtigløpende maskiner (høyt turtall, få poler) er “teknologien” høy. Vi har illustrert dette i Figur 43, hvor vi også har plottet inn to store maskiner.
Den ene maskinen som er plottet inn er Grand Coulee i USA som er 825 MVA, 85.7 opm, altså en meget stor maskin med lavt turtall. Den har en boring på ca. 21 m og en jernlengde på 2.1 m.
Utnyttelsesfaktor: C = 10.4
“Størrelse”: 9.62
“Teknologi”: 70.7
Den andre maskinen er vår egen Svartisen som er 410 MVA og 333 opm, dvs. en maskin med ca. halvparten av ytelsen i forhold til Grand Coulee, men med et tutall som er nesten 9 ganger større. Den har en boring på 5.8 m og en jernlengde på 2.8 m.
Utnyttelsesfaktor: C = 13.0
“Størrelse”: 1.23
“Teknologi”: 136
Disse tallene taler sitt eget språk som klart viser at vi i det lille landet Norge hvor en stor del av maskinene kan karakteriseres som hurtigløpere ikke på noen måte behøver å føle oss underlegne når det gjelder dette å mestre de tekniske utfordringene som vannkraftmarkedet gir oss.
6 Unormale driftspåkjenninge
Vi har i dette kurset valgt å definere begrepet unormale driftspåkjenninger som de påkjenninger maskinen blir utsatt for på grunn av driftsforstyrrelser som oppstår utenfor maskinen. De viktigste stedene slike forstyrrelser oppstår er nettet og turbinen, men vi har tatt med bla. fundamentet og magnetiseringsutstyret for å få et komplett bilde av de driftsforstyrrelser som er medtatt. Hvis alt skulle vært medtatt, skulle feks. apparatanlegg, kontrollanlegg, kjølevannstilførsel mm. vært med.
På Figur 44 er det vist en tabell over de viktigste driftsforstyrrelser, hvor de oppstår og hvor påkjenningene oppstår og hvilken kategori påkjenninger det er tale om. Tabellen er ikke fullstendig, men kan forhåpentlig være til noe hjelp likevel.
Vi skal nå gå gjennom de driftsforstyrrelsene som er vist i tabellen:
Kortslutning, stator
Kortslutnig på faseuttakene eller lenger ute på nettet vil medføre store kortslutningskrefter på statorviklingen, spesielt spolehode og støttesystemet for disse. Dessuten vil vi få et kortslutningsmoment som påkjenner innfestingen mot fundamentet og blikkpakkens innfesting mot statorhuset. Det samme skjer feks. mellom rotorring og nav og mellom nav og aksel. Store kortsluningskrefter oppstår også i dempeviklingens kortslutningslasker mellom polene.
Størrelsen på kortslutningskrefter og -momenter er avhengig av den samlede reaktans i kortslutningskretsen og kan dreie seg om 5 til 15 ganger det vi har i normal drift.
Feil synkronisering
Med dette tenker vi på at generatoren ved en feil blir faset inn på nettet med en for stor vinkel mellom generatorens og nettets spenningsvektorer. Det mest ekstreme er innfasing i motfase, dvs 180 o feilsynkronisering. Fenomenet arter seg på samme måte som for kortslutninger og virkningene er i prinsipp de samme.
Størrelsen på kreftene er avhengig av nettets kortslutningsytelse (reaktansen sett fra generatoren) og vinkelforskjellen mellom spenningsvektorene for generator og nett. I de ugunstigste tilfellene vil ikke generatoren tåle disse påkjenningene.
Skjevlast
Med dette mener vi at vi har en lastsituasjon som fører til ulik strøm i de tre fasene. Det mest ekstreme er at en fase fører null strøm mens de andre fører full strøm.
Hvis vi analyserer strømmen i de tre fasene i et skjevlasttilfelle ved hjelp av roterende vektorer, vil vi oppdage at i tillegg til de medroterende vektorene som vi har ved en symmentrisk last, har vi også fått vektorer som roterer den motsatte veien. Størrelsen av disse vektorene er større jo større skjevheten i lasten er. Disse vektorene vil indusere strømmer i dempeviklingen og gi årsak til oppvarming av denne. Sagt med andre ord så vil dempeviklingen sette opp en strøm som prøver å motvirke de motroterende strømkomponentene. Dette er forøvrig en av oppgavene for dempe-viklingen.
Overharmoniske spenningskomponenter
Dette er noe som oppstår på grunn av store likeretterlaster, feks. aluminiumsverk, eller last fra smelteverk. Størrelsen av de overharmoniske spenningskomponentene er avhengig av lastens størrelse og beskaffenhet og av nettets kortslutningsytelse sett fra generatoren.
Virkningen på generatoren er overharmoniske strømmer som blir indusert, primært i dempeviklingen, i poloverflaten og i statorblikkpakken. Dette gir sg utslag i økt temperatur i de samme delene. Å motvirke overharmoniske spenningskomponenter fra nettet er en annen oppgave som dempeviklingen har.
Atmosfæriske- og bryter-overspenninger
Dette er høye spenningsbølger som forplanter seg fra nettet inn mot generatoren. De er karakterisert ved en meget steil front, i størrelsesorden mikrosekund. Når denne meget hurtige spenningsøkningen eller spenningsgradienten entrer den første spolen i statorviklingen (den møter en reaktans), vil det oppstå store spenningsgradienter langs viklingen. Dersom det er en flervindingsspole, vil det oppstå en stor spenningsforskjell mellom spesielt den første og andre vindingen og det kan føre til gjennomslag mellom vindingene.
Også mellom vikling og jord vil det oppstå store spenninger, men her er isolasjonstykkelsen mye større, slik at faren for gjennomslag er mindre. Spenningsbølgen kan også forplante seg kapasitivt til feltviklingen og kan føre til gjennomslag også her.
Størrelsen av påkjenningen som generatoren utsettes for er avhengig av om feks. generatoren er koplet direkte til en linje, eller om det er en transformator mellom som er det vanligste i Norge. Det er også i mange tilfeller montert spenningsavledere som skal skjerme generatoren for slike overspenninger.
Asynkront løp
Dette kan skje hvis generatoren går med last og så mister magnetiseringen helt eller den blir redusert vesentlig. Da kan kippmomentet bli redusert til en verdi som er mindre enn det aktuelle lastmoment og vi får “polslipp” eller asynkronløp.
Asynkronløpet fører til at det oppstår et felt i luftgapet som roterer i forhold til rotor. (I synkron drift står feltet stille i forhold til rotor). Dermed “ser” polene et (til å begynne med lavfrekvent) vekselfelt og dette induserer strømmer i feltviklingen som kan gi opphav til overspenninger som igjen kan føre til overslag og/ eller varmgang. Etter hvert som rotoren retarderer, øker frekvensen som polene ser og dempeviklingen vil få mer og mer “juling”.
Overturtall
Dette kan skje ved reguleringsfeil eller ved lastavslag. Alle generatorer er dimensjonert for å tåle dette, men hvis det skjer meget hyppig, må en sjekke rotorkomponentens evne til å motstå slike lastsykler over lengre tid.
Lagrene vil få høyere temperatur på grunn av turtallsstigningen. Oljefilmtykkelsen vil øke, slik at faren for at lageret skal skjære seg derimot ikke er særlig overhengende.
Ubalanse i turbin
Ubalanse kan selvfølgelig også oppstå i generatoren, men her har vi definert driftsforstyrrelser som de som oppstår utenfor generatoren. Ubalanse fører til vibrasjoner og disse får innvirkning på alle roterende deler samt på lagrene, spesielt styrelagrene og fører til temperaturstigninger der.
Setninger i fundamentet
Setningen kan føre til forskyvninger i bunnklossene for statorhuset eller lagerarmkryss. Konsekvensen er at rotor kan bli stående eksentrisk i stator eller at akselopprettingen kommer ut av stilling slik at lagrene “kniper” om akslingen.
Luftgapseksentrisiteten fører til usymmetrisk magnetisk trekk mellom rotor og stator med derav følgende større styrelagerbelastning, noe som medfører temperaturøkning.
At lagrene “kniper” kan føre til ujevn temperaturfordeling på akselomfanget og akselen kan slå krok som igjen fører til større knip og dermed større krok, osv. Resultatet er vibrasjoner og temperaturstigning på lagrene.
7 Utviklingstrekk
7.1 Materialer/prosesser/design
I løpet av de ca. 100 år som er gått etter at de første maskinene ble montert her i landet har det skjedd en kolossal utvikling på materialsiden. Materialer med stadig bedre egenskaper og jevnere kvalitet har blitt utviklet. Dette gjelder de fleste materialer, vi kan nevne støpestål, smigods, valset stål, “elektroblikk” for statorblikkpakken, kunstharpiksmaterialer for viklingsisolasjon, glassfiberarmerte kunstharpikser for kapslinger og sporkiler, etc.
Dessuten er nye produksjonsprosesser utviklet i takt med de nye materialene: sveiseteknikk, lakkisolerte statorblikk, vakuum- impregnert kunstharpiks- statorisolasjon, etc.
I tillegg har det blitt utviklet stadig gunstigere konstruksjoner og sikrere beregningsprogrammer for de påkjenningene som de utsettes for. F. eks. FINITE ELEMENT analyseprogrammer som på en helt annen måte enn før kan kartlegge spiss-spenninger og påkjenninger ved dynamiske forhold. Samtidig har kvalitetskontrollen blitt bedre og sikrere. Det samme gjelder systemene for kvalitetssikring.
Statorviklingen
Hvis vi går mer i detalj og ser på hvordan denne utviklingen har påvirket de enkelte maskinkomponentene, vil isolasjonssystemet for stotorviklingen utpeke seg som kanskje det mest iøynefallende området hvor utviklingen har fått avgjørende betydning.
Etter hvert som en har fått mer kunnskap om aldringsmekanismene har det skjedd en suksessiv overgang til mer aldringbestandige materialer. Og dette gjelder ikke bare aldringsegenskapene, men andre tekniske egenskaper har også blitt bedre.
Vakuumimpregnering av statorstavene var en viktig milepæl og senere kom kunstharpiks-isolerte staver. I løpet av denne tiden har en kunnet øke feltstyrken på sporisolasjonen til minst det dobbelte og tillatt maksimal temperatur har kunnet høynes vesentlig. Også på områder som glimbeskyttelse, sporkiler, støttemateriell, lodde/ sveise- metoder har utviklingen vært stor. I tillegg har vi også fått avanserte programmer for beregning av kortslutningskrefter på spolehodene som muliggjør en optimal dimensjonering oppstøttingssystemet.
Statorblikk
Noe av det samme har skjedd for statorblikkjernen. Tapstallet (kW/kg) for blikket har blitt redusert vesentlig, fra 2.7 til 1.0 W/kg og overgangen fra papirisolerte til lakkisolerte blikk har gitt oss en mer aldringbestandig og temperaturbestandig isolering. Nye beregningsprogrammer (Finite Element) har satt oss i stand til å unngå vibrasjonsproblemer, feks. pressystemet for blikkpakken er forbedret idet vi nå ofte benytter gjennomgående pressbolter direkte gjennom blikket istedet for at boltene er plassert utafor ryggen av blikket. Dette gir et mer kontrollert, sikrere og mer stabilt og homogent press, som gir stor stabilitet, f.eks. mot “buckling”.
Rotorviklingen
Når det gjelder rotorviklingen er vel det vesentligste som har skjedd at temperaturklassen er øket fra klasse A til klasse F, slik at vi nå er på høyde med statorviklingen. Den miljøfarlige asbest- isolasjonen er skiftet ut med NOMEX som ikke er helsefarlig og har like gode elektriske og termiske egenskaper.
Magnetiseringsutstyr
De roterende likestrøms magnetiseringsmaskinene med
tilhørende
spenningsregulatorer av “tikkende” eller “valsende” type,
transduktorregulator, el.l. har blitt erstattet av statiske
tyristor- systemer, med helt andre reguleringsmuligheter og med
mindre vedlikeholdskostnader.
Vi nevner også muligheten for børsteløst magnetiseringssystem
som må sies å være nesten vedlikeholdsfritt.
Hovedeffekten leveres fra en “speilvendt” synkrongenerator der
ankerviklingen er plassert på rotoren og er koblet til
generatorens polvikling via
roterende dioder. Reguleringen foretas på den stasjonære
polviklingen ved hjelp av en elektronisk regulator. Dette kan være
et gunstig alternativ også til statisk magnetisering og er
spesielt interessant for ombygging av gamle maskiner med LS
magnetiseringsmaskin. Her er det plass nok til den nye VS-
magnetiseringsmaskinen og en trenger svært liten plass til
spenningsregulatoren som ellers ville kunne være et problem å få
plass til ved ombygging til statisk magnetisering.
Lagre
Også når det gjelder lagrene har det skjedd en viss utvikling. Vi kan feks. nevne selvsmørende lagre, hvitmetallbelagte vippesegmenter, separate oljekjølere, bedre og mer komplette overvåkingsorganer, osv. Vi må også trekke fram trykkoljeavlastningen på bærelagrene som har blitt standard på alle bærelagre og som i høy grad har bidratt til økt levetid og større driftssikkerhet.
Det eksperimenteres med Teflon-belagte segmenter som krever mindre oljesmøring og dermed tap.
Bedre beregningsprogrammer har bidratt til en mer optimal dimensjonering slik at tapene blir minimalisert samtidig som min. ojlefilmtykkelse sikres og temperaturene ikke overstiger tillatte grenser.
Vi vil også nevne et relativt nytt konsept med pumpesegmenter. Disse er plassert i radialdelen av lageret og sørger for oljesirkulasjon både til radial- og aksiallageret slik at vi får et selvpumpende lager. Dermed får man et meget sikkert og vedlikeholdsfritt system idet en unngår pumper med styringer og overvåkning, og en får et enklere rørsystem. En er også sikret nødvendig oljetilførsel i krisesituasjoner ved feil og strømbrudd, noe som en ellers må ta hensyn til.
Ventilasjonssystemet
Ventilasjonssystemet har også gjennomgått en utvikling som vi bør ta fram her.
Overgangen fra friskluftkjøling til omluftkjøling betydde renere maskiner og dermed mindre vedlikeholdsarbeid. Men det har kanskje ikke minst medført muligheter for temperaturkontroll, slik at en kan unngå for store temperatursvingninger over døgnet og året. Også her har sikrere beregningsprogrammer blitt utviklet, noe som har gjort det mulig å effektivisere kjølingen samtidig som ventilasjonstapene kan reduseres.
Vi vil her i tillegg nevne ventilasjonskonseptet “ventilert ring” som er beskrevet under pkt. 5.1. Fordelen med dette er at en unngår de tradisjonelle, påbygde viftebladene og oppnår en meget jevn og effektiv kjøling av både rotor og stator.
Listen på komponenter som har gjennomgått en vesentlig utvikling kunne selvsagt ha blitt gjort mye lengre, men dette får greie seg i denne omgang. På Figur 46 er noen av de viktigste milepælene listet opp.
På 80-90 talet har utviklingen forsatt, om enn ikke i samme tempo som i perioden 1960-1980.
Utviklingen har primært vært rettet mot utvikling av bedre beregningsmetoder, Finite Element beregninger for mekaniske spenninger, magnetiske felter samt ventilasjonssystemer.
Av direkte teknisk nyvinninger kan nevnes:
- “Oblique elements” for mekaniske støttekonstruksjoner med stor diameter.
- Maskiner med høyspente statorviklinger, 45-150 kV.
7.2 Utnyttelsesfaktor
Den utvikling som har skjedd for materialer og tilvirkingsprosesser har muliggjort høyere utnyttelsesfaktor for maskinene. Som vi så i Kapittel 4 er utnyttelsesfaktoren et mål for den ytelse som legges inn i boringsvolumet.
Som vi har sett i Kapittel 4 betyr høy utnyttelsesfaktor (ved et bestemt turtall) at ytelse pr. volumenhet av maskinen er høyt idet vi i Kapittel 4 fant
\[C = S/(D^2 \cdot L \cdot n)\qquad{(68)}\]
se Formel 55
og ved å innføre volumet av statorboringen V = π/4(D2 • L) :
\[C = k_1 \cdot (S/V)/n\qquad{(69)}\]
Undersøker vi utviklingen fra 1940 til idag, så vil vi se at økningen er ca. 100%. Dette innebærer at boringsvolumet på en moderne generator kan være bare halvparten av det som en generator med samme ytelse og turtall fra 1940- tallet har. På slutten av 60- tallet kom de første direkte vannkjølte generatorene og utnyttelsesfaktoren gjorde dermed et hopp oppover på ca. 50%. På Figur 47 har vi forsøkt å anskueliggjøre utviklingen.
Denne utviklingen har dog ikke utelukkende tatt sikte på høyere utnyttelse, men har også innebåret at vi på flere områder har fått både mer driftsikre og mer service-vennlige maskiner. Det er også en kjensgjerning at kravet til svingmasse har hatt en synkende tendens opp gjennom årene, og det har selvsagt ført til at boringsvolumet har kunnet reduseres noe.
Disse mulighetene som utviklingen har ført med seg kan vi også i større eller mindre grad nyttiggjøre oss ved oppgradering, opprustning og modernisering av eldre generatorer.
Vi skal nå se litt på hvordan økt utnyttelse fører til økte materialpåkjenninger.
Termisk belastning
Vi skjønner at jo høyere utnyttelsesfaktor, jo vanskeligere blir det å bli kvitt tapsvarmen rett og slett fordi tapene blir konsentrert i et mindre volum eller mindre flater.
La oss se nærmere på storviklingen:
Dersom vi innfører ankerbelastningen As som er ampereledere pr. cm av boringsomfanget:
\[As = I_n \cdot Q \cdot (N_s/c)/ \pi \cdot D\qquad{(70)}\]
og magnetisk feltstyrke i luftgapet, Bδ1, kan det lett utledes at utnyttelsesfaktoren blir proporsjonalt med produktet av As og Bδ1:
\[C = k_2 \cdot A_s \cdot B_{\delta 1}\qquad{(71)}\]
Vi ser at høy utnyttelse betyr vanskeligere kjøleforhold for statorviklingen idet konsentrasjonen av koppertapene på statoromfanget grovt sett vil være proporsjonal med kvadratet av anker belastningen.
Det skal dog bemerkes at forholdene i realiteten ikke er fullt så enkle som at temperatur og utnyttelse henger entydig sammen. En av grunnene til dette er at økt utnyttelsesfaktor gjerne medfører noe større diameter, med derav bedrede ventilasjonsforhold. En annen viktig grunn er at den moderne isolasjonsvegg er vesentlig tynnere enn den gamle og termisk ledningsevne er bedre slik at varmetransporten mellom kopper og blikk har blitt vesentlig bedre.
Magnetisk feltstyrke
Vi vil også lett forstå at når boringsvolumet minker, vil magnetisk feltstyrke i luftgapet øke under ellers like forhold siden fluksen, som er konstant, får en mindre flate å strømme gjennom. Dette vil ikke bare gjelde luftgapet, men også statortenner, statorrygg og poler siden feltstyrken her er proporsjonal med feltstyrken i luftgapet.
Matematisk ser vi dette av uttrykk Formel 71 som sier at luftgapsinduksjonen er proporsjonal med utnyttelsesfaktoren:
\[B_{\delta 1} = (1/k_2) \cdot C/A_S\qquad{(72)}\]
(Spillerommet for luftgapsinduksjonen B1 er begrenset: 0.8 - 1.1 Tesla)
Jerntapene er i prinsipp proporsjonal med kvadratet på magnetisk feltstyrke og proporsjonalt med tapstallet for blikket. Selv om utviklingen har ført til økte feltstyrker kan vi vel si at reduksjonen av tapstallet som har skjedd minst har kompensert for dette.
Mekaniske spenninger
Høy utnyttelsesfaktor betyr også høyere mekaniske påkjenninger
i rotor. Dette kommer av at under ellers like forhold (feks. samme
svingmasse) vil økt utnyttelsesfaktor føre til en økning av
diameteren. Dermed skjønner vi at økt utnyttelse fører til
større
sentrifugalkrefter og dermed større mekaniske spenninger.
Av uttrykket Formel 60 :
\[D = \sqrt( (\theta \cdot C \cdot n)/(\beta \cdot S) )\qquad{(73)}\]
ser vi at diameteren øker med utnyttelsesfaktoren.
7.3 Konklusjon
I løpet generatorenes historie har det skjedd en radikal utvikling av bedre og mer homogene materialer, nye og sikrere tilvirkingsprosesser, gunstigere konstruksjoner, sikrere beregningsprogrammer og bedre kvalitetskontroll- og styring. Dette har gjort det mulig å øke utnyttelsesgraden av maskinene, slik at vekt, dimensjoner og dermed kostnader både for maskin og kraftstasjon har kunnet reduseres. Dette har skjedd med økt kvalitet og bedre virkningsgrad.
Dette viser også at mulighetene når det gjelder oppgradering og opprustning av eldre maskiner burde meget store, både teknisk og økonomisk.
8 Aldring/Levetid
Alle materialer aldres eller svekkes under påvirkning av påkjenninger over tid. Det kan være temperatur, elektrisk feltstyrke, mekaniske spenninger (statiske og dynamiske), kjemiske påvirkninger (feks. vann, luft, gasser), slitasje, etc. I de følgende delene der en tar for seg de enkelte komponentene vil dette bli beskrevet mer i detalj. Her vil vi bare peke på kompleksiteten i de påkjenninger som oppstår under drift. Det er f.eks. ikke slik at levetiden for en statorvikling utelukkende er bestemt av temperaturnivået for viklingen. Mekaniske og elektriske påkjenninger kan spille like stor rolle , feks. vibrasjoner, termiske deformasjoner ved feks. hyppig start og stopp, glimming (høy elektrisk feltstyrke i overflaten), osv.
Spørsmålet om restlevetid for de forskjellige komponentene er et tema som har vært oppe til debatt i både internasjonale og mer hjemlige fora gjennom mange år, kanskje spesielt de siste 5- 6 årene. Det er klart at hvis en kunne skaffe seg en pålitelig oversikt over dette, så ville vedlikehold og utskiftninger kunne planlegges på den mest optimale måte for å oppnå en størst mulig forlengelse av aggregatets levetid.
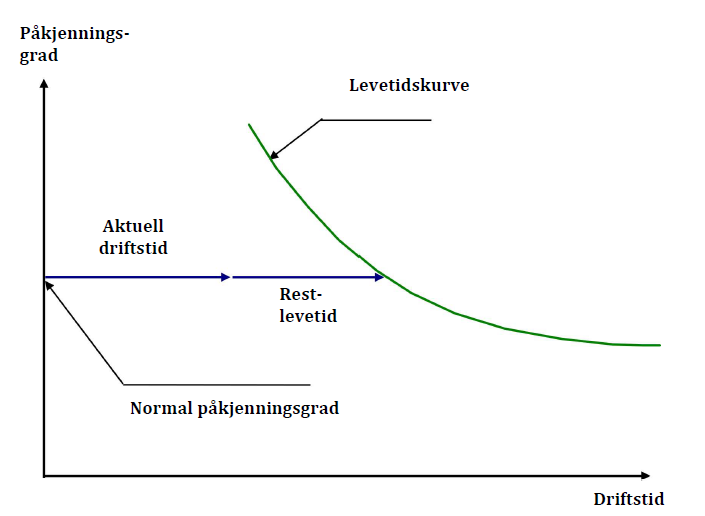
Noen har forsøkt seg med “enkle” betraktninger, feks. for statorviklinger, der restlevetiden kan beregnes ut fra en enkle betraktinger om skademekanismer og de påkjenninger som viklingen utsettes for under drift. En illustrasjon av dette kan ses på Figur 48. Her kan en tenke seg at en har beregnet en “levetidskurve” for feks. statorisolasjonen som funksjon av driftstid og “påkjenningsgrad”. Restlevetiden kan dermed leses rett ut av diagrammet. Problemet er både å utvikle en pålitelig levetidskurve og å beregne summen av de påkjenninger som viklingen har vært utsatt for inntil dags dato slik at den midlere påkjenningsgrad kan bestemmes. Vi må vel erkjenne at dette blir mer komplisert og resultatet mer usikkert enn det en kan gjøre seg praktisk nytte av.
Likevel er det meget viktig å skaffe seg den best mulige oversikt over de mekanismer som bryter ned feks. statorisolasjonen basert både på teoretiske betraktninger og erfaringer fra både laboratorieforsøk og fra driften. Det er også viktig å samle data for driftspåkjenningene over levetiden, men her forstyrres bildet i vesentlig grad av kompleksiteten av de mange ytre påkjenninger som delen utsettes for. Her kommer ikke bare normalpåkjenningene inn, men størrelsen av ekstraordinere påkjenninger, kombinasjonen med andre påkjenninger, tidspunktet når de inntreffer og hvor mange ganger før de har inntruffet, osv. På Figur 49 er dette forsøkt anskueliggjort.
Som sagt er kunnskapen om skade/ nedbrytningsmekanismene og
registrering/ innsamling av de påkjenningene som maskinen har vært
utsatt for meget viktig. Dette er helt nødvendig for å kunne gjøre
seg opp mening om maskinens tilstand ut fra målinger og for å
kunne foreta de riktige beslutninger. Hvordan dette bør gjøres vil
bli behandlet i de andre delene av dette kurset der en gjennomgår
de enkelte komponentene. Her vil vi bare nevne at en spesielt er
ute etter trender av
tilstandsutviklingen. Det ligger også i kortene her at desto
sterkere trenden er, desto hyppigere bør tilstanden måles. Dette
er etter vår mening en sikrere metode enn bare å se på det
absolutte tilstands- og påkjenningsnivå.
Kombinert med en solid kunnskap om skade/ nedbrytningsmekanismene og det brede erfaringsunderlag som finnes på området vil dette gi det beste grunnlaget for en prognose for restlevetiden og for en sikker beslutning angående videre tiltak.
9 Figurer










ANTALL POLER, TURTALL OG FREKVENS
| Generell regel | n = f120/(2p)* | n = 6000/(2p) |
| f = 50 Hz | 2p = f120/n* | 2p = 6000/n |
n: Turtall (o.p.m) f: Frekvens (Hz) 2p: Antall poler (-)













BESTEMME HOVEDDIMENSJONENE, Eksempel
| Ytelse |
|
| Svingmasse |
|
| Turtall (Nom) |
|
| Turtall (Rusn.) |
|
Poltall: 2p = 6000/n = 6000/600 = 10 poler
Polytelse: S/2p = 50/10 = 5 MVA/pol
Utnyttelsesfaktor (Fra kurve): C = 6.8
Svingmassefaktor (Fra kurve): b = 2.5
Diameter (likning Formel 60 ):
\[D = sqrt[(Q \cdot C \cdot n) / (b \cdot S)] = 2.92 m\qquad{(74)}\]
Valgt: 2.6 m
Lengde (likning Formel 61 ):
\[L = (S/C \cdot n)2 \cdot b /Q = 1.69 m\qquad{(75)}\]
Valgt: 2.0 m
Periferihastighet (Rusn.):
\[V_r = \pi \cdot D \cdot n_r/60 = 168 m/s\qquad{(76)}\]
Vanligvis prøver en å unngå periferihastigheter over 150 m/s fordi det ofte fører til økte kostnader å hanskes med de tilsvarende mekaniske påkjenningene. Derfor gikk en i dette tilfellet ned til 2.6 m i diameter og måtte dermed øke lengden for å begrense ytnyttelsesfaktoren. I et generelt tilfelle må dette overveies nøye ved hjelp av komplette beregninger. Her må også transport- og montasjeforhold vurderes.
BESTEMME HOVEDDIMENSJONER
Gitt:
Ytelse - Turtall - Svingmasse - Ruseturtall
Bestem poltall ut fra turtallet
Bestem ytelse pr. pol
Bestem utnyttelsesfaktor og svingmassefaktor
Kombiner formlene for svingmasse og utnyttelsesfaktor for å bestemme boringsdiameter og jernlengde
Sjekk periferihastigheten
Vurder:
- Transportdimensjoner
- Montasjeforhold - bygningsmessig tilpasning
- Kritisk turtall
- Utnyttelsesfaktoren i lys av kravene til reaktanser og
- Tapskapitalisering


“STØRRELSE” OG “TEKNOLOGI”
• «Størrelse» = S/n (MVA/o.p.m)
\[C = S/(D^2 \cdot L \cdot n)\qquad{(77)}\]
som gir
\[S/n = C \cdot D^2 \cdot L = k \cdot V\qquad{(78)}\]
der V er boringsvolumet og k er en konstant
«Størrelse» = k • C • V (MVA/o.p.m)
• «Teknologi» = Sn/1000 (MVA/pol)
med n = 6000/2p
«Teknologi»= 6 • S/2p (MVA/pol)
| S [MVA] n [o.p.m] L [m] C «Utnyttelse» «Størrelse» «Teknologi» |
Grand 852 86 21 10,4 9,62 71 Coulee
9.1 Svartisen 410 333 5,8 2,8 13 136



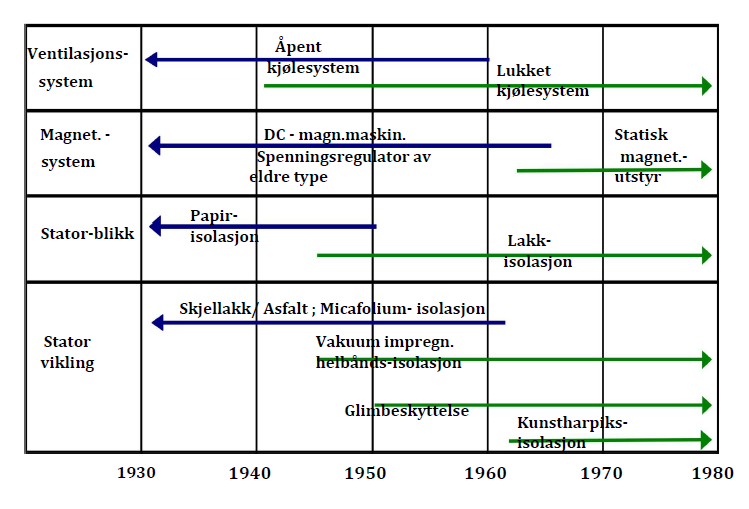
Om milepæler i generatorviklinger:
På 80-90 tallet har utviklingen fortsatt, om enn ikke i samme tempo som i perioden 1960-1980.
Utviklingen har primært vært rettet mot utvikling av bedre beregningsmetoder, Finite Element beregninger for mekaniske spenninger, magnetiske felter samt ventilasjonsystemer.
Av direkte teknisk nyvinninger kan nevnes:
- “Oblique elements” for mekaniske støttekonstruksjoner med stor diameter.
- Maskiner med høyspente statorviklinger, 45-150 kV.

MATERIALER OG PROSESSER - Historisk utvikling
Konklusjon:
Radikal utvikling av:
- bedre og mer homogene materialer
- nye og sikrere tilvirkingsprosesser
- gunstigere konstruksjoner
- sikrere beregningsprogrammer
- og bedre kvalitetskontroll- og styring
Dette har muliggjort økning av utnyttelsesgraden av maskinene som medfører reduksjon av:
vekt
dimensjoner og dermed
- kostnader for maskin
- kostnader for kraftstasjon (Volum)
Dette har skjedd med økt kvalitet og bedre virknings- grad.
Mulighetene når det gjelder oppgradering og opprusting av eldre maskiner er derfor meget store, både teknisk og økonomisk.