5 Sikkerhetsfaktorer
5.1 Sikkerhetsfaktorer generelt 5.2 Damforskriftene 5.3 TBK og Rules for Certification of Diving Systems 5.4 “Finite elements”-beregning 5.5 Avledete størrelser 5.6 Eksempel: Vannlast 5.7 Eksempel: Dimensjonerende spenning6 Krefter og belastninger
6.1 Belastningstyper 6.2 Belastninger for innstøpt platekasse 6.3 Innstøpte rør 6.4 Frittliggende rør 6.5 Friksjonskrefter 6.6 Istrykk 6.7 Temperaturvariasjoner og temperaturkrefter 6.8 Trafikkbelastninger 6.9 Krefter i fagverk7 Strekk- og trykkspenning
7.1 Normalspenning 7.2 Flatetrykk for glidelister 7.3 Hjultrykk 7.4 Flatetrykk mot betong 7.5 Membranspenninger i sfæriske og sylindriske skall 7.6 Eksempel: Aksialspenning i gjenget bolt 7.7 Eksempel: Membranspenninger i rør8 Enakset bøyespenning
8.1 Bøyebelastning for bjelke 8.2 Plate opplagret på bjelker 8.3 8.4 Eksempel: Spenninger i frontplate på tvers av bjelkeretning 8.59 Toakset bøyespenning i plate
9.1 Generelt 9.2 Rektangulære platefelt 9.3 Rondeller og ringplater 9.4 Eksempel: Rørflens regnet som ringplate11 Skjærspenning pga. skjærkraft
11.1 Aktuelle formler 11.2 Skjærkraft ved nagle- og boltforbindelse 11.3 Eksempel: Skjærspenning mellom bjelke og frontplate12 Vridningsspenning (torsjon)
12.1 Vridningsspenning i enkle profiler 12.2 Vridningsspenning i lukkede tynnveggede tverrsnitt 12.3 Vridningsspenning i åpne tynnveggede tverrsnitt 12.4 Vridningsspenning i mindre klappeluke16 Utmatting
16.1 Konstruksjoner hvor utmatting bør undersøkes 16.2 Utmattingsdiagrammer 16.3 Egensvingning ifm. varegrinder 16.4 Egensvingning ifm. platekasser 16.5 Eksempel: Egensvingefrekvens for grindstav17 Bruksgrensetilstand
17.1 Generelt om bruksgrensekontroll 17.2 17.3 Eksempel: Kontroll av deformasjon for glideluke 17.4 Eksempel: Kontroll av deformasjon for klappelukeHÅNDBOK - MEKANISKE KONSTRUKSJONER I VANNVEIEN: DIMENSJONERING AV UTSTYR I KRAFTVERKSVANNVEIEN
1 Innledning
Forfatter: Ragnar Hartmann, Statkraft Engineering as 12.03.96
Dette manuskript er betalt av Energiforsyningens Fellesorganisasjon (EnFO) og kan fritt benyttes ved alle EnFOs nåværende og fremtidige kurs. Bruk til andre formål, omarbeidelser eller videre bearbeiding, krever forfatters godkjennelse. Statkraft Engineerings eventuelle bruk av manuskriptet skal ikke skje slik at dette kommer i konkurranse med EnFOs virksomhet. Privatpersoner har anledning til å ta enkeltkopier når for- målet er egen opplæring. Ved kopiering ut over dette for andre enn EnFO, Statkraft Engineering eller forfatter, må tillatelse på forhånd være innhentet fra EnFO.
2 Hensikt og målsetting
Manuskriptet er laget i tilknytning til et kurs om luker, ventiler, rør og varegrinder. Primært mål er å øke forståelsen for hvordan en konstruksjon kan analyseres styrkemessig. Sekundært vil manuskriptet ved presentert tekst og litteraturhenvisninger kunne hjelpe den som måtte ønske å tilegne seg mer kunnskap.
Kursets målgruppe er personell ved vannverk og i kraftforsyning. Manuskriptet har imidlertid delvis blitt skrevet for den del av gruppen som har bygnings- eller maskiningeniørkompetanse. Det er likevel et håp at eksemplene som illustrerer det presenterte stoff, reduserer terskelen til forståelse.
Manuskriptet presenterer ulike konstruksjonstyper og belastningssituasjoner, men fremstillingen er ikke komplett, og det gis ingen teoretisk bakgrunn for presenterte formler. Av disse årsaker frarådes at man benytter manuskriptet ved dimensjonering uten samtidig å ha grunnleggende forståelse av hva som gjøres. Ved beregninger som kan bli av betydning for sikkerhet eller økonomi må manuskriptet ikke benyttes som referanse. For dette anbefales litteraturlistens titler.
3 Symboler
Anvendte symboler er sammen med aktuelle måleenheter angitt i listen nedenfor. I flere tilfeller avviker disse symboler fra symbolene i de referanser formler er hentet fra. Årsaken er at man i manuskriptet har tilstrebet ensartet symbolbruk.
a - lengde (mm).
b - lengde (mm).
d - diameter (mm).
f - friksjonseksentrisitet ved rullemotstand (mm).
fHz - svingefrekvens (s-1).
i - treghetsradius = (I/ A)0,5 (mm).
ks - sikkerhetsfaktor, forhold mellom “bruddlast” og tillatt last. Belastningen kan være kraft, trykk eller antall belastningsvariasjoner (ubenevnt).
l - lengde (mm).
lk - knekklengde for stav (mm).
m - forholdststall mellom lineære dimensjoner (ubenevnt).
n - antall belastninger (stk), eller svingemode.
p - flatetrykk, ev. vanntrykk (MPa).
q - belastning langs bjelke, etc. (N/mm).
r - radius (mm)
t - tykkelse(mm).
x - variabel lengde (mm).
A - areal (mm2).
B - profilbredde (mm).
D - platestivhet = E • t2 / ( 12 • (1-v2)) (N).
E - elastisitetsmodul (MPa).
F - kraft (last) (N).
Fb - “bruddlast” for konstruksjon/struktur (N).
Fd - dimensjonerende last for konstruksjon/struktur (N).
Ft - tillatt bæreevne (last) for konstruksjon/struktur (N).
G - skjærmodul (MPa)
H - profilhøyde (mm).
I - treghetsmoment (mm4).
Ip - polart treghetsmoment (mm4).
M - bøyemoment (Nmm).
Mv - vridningsmoment (Nmm)
Q - skjærkraft (N).
T - flatemoment (mm3)
W - motstandsmoment (mm3).
Wp - polart motstandsmoment (mm3).
α - lineær temperaturutvidelseskoeffisient (°C-1).
ε - relativ forlengelse (ubenevnt).
γf - lastfaktor (i Damforskriftene kallt lastkoeffisient) (ubenevnt).
γm - materialfaktor (i Damforskriftene kallt materialkoeffisient) (ubenevnt).
γv - deformasjonsvinkel knyttet til skjærspenning og skjærmodul (ubenevnt).
δ - lineær deformasjon (mm).
φ - faktor for beregning av spenning i rektangulær eller sirk. plate (ubenevnt).
φv - resulternede deformasjonsvinkel pga. vridning (ubenevnt, dvs. radianer).
λ - slankhet = lk/i (ubenevnt).
λre - relativ slankhet = (λ/π)-(σF/E)0,5 (ubenevnt).
μ - friksjonskoeffisient (ubenevnt).
ν - Poissons konstant (ubenevnt).
ρ - densitet (kg/m3).
σ - strekk-, trykk- eller bøyespenning (MPa).
σd - dimensjonerende spenning = σF / γm (MPa).
σk - knekkspenning (MPa).
σkre - relativ knekkspenning = σk / σF (ubenevnt).
σB - bruddspenning (strekkgrense) (MPa).
σE - Euler-spenning = π2 • E/λ2 (MPa).
σF - flytespenning (MPa).
σ0,2 - spenning som etter avlastning gir 0,2 % varig forlengelse (MPa).
τ - skjærspenning (MPa)
τv - vridningsspenning (MPa).
4 Dimensjonering og regelverk
Ved dimensjonering fastlegges eller verifiseres en konstruksjons dimensjoner. Dimensjoneringen kan karakteriseres som en teoretisk undersøkelse av pålitelighet, funksjonalitet og økonomi. Mest fokusert blir vanligvis sikkerhet mot brudd.
Brudd-dimensjonering gjennomføres i overenstemmelse med regler, dimensjonerings- standarder og forskrifter. For kraftverksluker i Norge anvendes Damforskriftene med tilhørende regler og NS 3472. Ifm. kraftverksrør av stål nyttes TBK. Mange byggherrer stiller dessuten egne krav i tillegg til de forannevnte.
Det er et faktum at Norges handelspolitiske tilnærming til det øvrige Europa med intensjon om fri flyt av varer og tjenester, aktualiserer bruk av andre beregningsstandarder enn de forannevnte. Dette sammen med det at ny forskrift skal avløse Damforskriftene, medfører at man i dette manuskript har valgt å dempe bindingen til forskrifter og standarder.
For beregninger som kan komme i tillegg til vanlig bruddkontroll, er det få generelle retningslinjer. Ofte må man ved slike problemstillinger etter beste skjønn selv forsøke å utarbeide noe som blir både korrekt og anvendbart, men de to hensyn lar seg til tider vanskelig forene. Eksempler på slike andre aktuelle beregningsoppgaver listes nedenfor. Nærmere behandling av de nevnte beregningene vil ikke bli gitt i dette manuskript.
Økonomisk dimensjonering.
Pålitelighetsanalyser.
Vannføringsberegninger.
Beregning av luftbehov for luker og ventiler.
Temperaturberegninger (kontroll vedr. innvendig ising i frittliggende rør).
Ved ny konstruksjon er det en god regel å utforme strukturer slik at de ikke blir for kompliserte å beregne. Ifm. eldre konstruksjoner må man imidlertid ta de utfordringer som er. Det skal ikke legges skjul på at enkelte eldre konstruksjoner tidligere er behandlet noe lettvint. Ved de revurderinger som NVE krever skal gjennomføres i tilknytning til enkelte hovedtilsyn, er intensjonen at konstruksjonene skal vurderes mot dagens krav. Dette betyr at beregningsdokumentasjon også skal foreligge og at den om nødvendig må utføres på nytt. For den som revurderer, må det derfor stilles strenge krav til teoretisk kompetanse. Det forekommer eksempelvis at det ifm. eldre utstyr blir aktuelt å benytte bruddmekanikk. Slik teori kommer sjelden til anvendelse ved dimensjonering av nytt utstyr.
I spesielle tilfeller mener undertegnede det kan føre galt avsted å benytte moderne dimensjoneringsstandarder for evaluering av eldre utstyr. Dette gjelder særlig når utstyret skal utbedres eller modifiseres. Dagens standarder forutsetter moderne materialer med krav til seighet og sveisbarhet. For det eldre utstyret ble materialvalgene gjort i en tid da sveising var uaktuell som vanlig sammenføyningsmetode samtidig som man manglet egnet verktøy for teoretisk vurdering av sprøbrudd og utmatting. Ifm. dimensjonering og gjennomføring av konstruksjonsendringer på eldre konstruksjoner fremsettes derfor følgende råd:
Vær varsom med å gå høyt i spenningsnivå.
Belast ikke plater med strekkspenninger i tykkelsesretningen.
Vurder all sveising i eldre bærende strukturer før sveisingen gjennomføres. Stikkord: Sveisbarhet og innspenningsforhold.
Gjør tiltak som bidrar til nødvendig reduksjon av sprøbruddrisiko. Stikkord: Forhøyet arbeidstemperatur og avspenningsglødning.
Ved bruk av moderne beregningsstandarder bør resultatene sammenholdes med generell teori. Vær klar over at eldre sprø materialer har mindre evne enn de moderne til å la spenningsspisser avlastes ved flyting.
5 Sikkerhetsfaktorer
5.1 Sikkerhetsfaktorer generelt
Forståelse av hva som menes med sikkerhet og hva en sikkerhetsfaktor egentlig er, bør den ha som ved dimensjonering er nødt til å bevege seg utenfor merket løype. “Sikkerhet” som emne er imidlertid behandlet i manuskriptet “Sikkerhets- og pålitelighetsteknikk. I det etterfølgende begrenser en seg til å drøfte sikkerhetsfaktoren k, hvor betegnelsen”sikkerhet” har lite å gjøre med tilsvarende betegnelse i faget “sikkerhetsteknikk”.

Sikkerhetsfaktoren knyttes som regel til bruddsikkerhetsverifikasjonen for en konstruksjon eller struktur og kan være forholdet mellom bruddlast FB og tillatt last Ft. I noen tilfeller erstattes kraftforholdet med et tilsvarende trykkforhold eller forhold mellom belastningscykler. I beregninger fremkommer ks ofte som forholdet mellom flytespenning og tillatt spenning, referert til dimensjonerende belastning.
Sikkerhetsfaktorens størrelse kan variere fra en dimensjoneringsstandard eller regelverk til et annet. I Figur 1 sammenstilles sikkerhetsfaktorer fra ulike referanser. Korrosjonsfradraget som vanligvis benyttes for vannkraftutstyr utført i ulegert/lavlegert stål, kommer som tillegg og vil i praksis ved egnet korrosjonsbeskyttelse og ansvarlig vedlikehold øke sikkerhetsfaktoren noe.
Størst sikkerhetsfaktor er tradisjonelt anvendt ved turbindimensjonering. Lavest verdi får | man når vanlige stålkonstruksjonsstandarder anvendes. Damforskriftene med sine regler og anbefalinger faller mellom Trykkbeholderbestemmelsene (TBK) og Veritas: “Rules for Certification of Diving Systems, 1988” (RCDS). Dog spesifiserer Damforskriftene generelle minimumskrav. Hvor spesielle forhold tilsier det, kan det være riktig å endre sikkerhetsfaktoren ift. Damforskriftenes krav.
Det må imidlertid påpekes at sikkerhetsfaktoren ikke nødvendigvis uttrykker sikkerhetsnivået for de konstruksjoner den anvendes for. Vel så ofte sier sikkerhetsfaktoren noen om beregningsnøyaktigheten. Av denne grunn kan det også hevdes at betegnelsen sikkerhetsfaktor er misvisende. Et bedre uttrykk ville vært usikkerhetsfaktor. Ved knekkberegninger hvor både beregningsmessig og faktisk bruddgrense knyttes til flyting, har det således vært vanlig å operere med noe høyere sikkerhetsfaktor enn det man tilsvarende gjør for en tilstand med ren strekkspenning. For sistnevnte tilfelle blir flytegrensen den beregningsmessige bruddgrense, mens virkelig brudd ofte skjer først når materialspenningen har nådd bruddspenning.
5.2 Damforskriftene
Damforskriftenes “gule” tilleggsdel med dimensjoneringsregler, bygger for ståldelers vedkommende på NS 3472, men viser også til DIN 19704. Sistnevnte standard spesifiserer ulike sikkerhetsfaktorer avhengig av materialspenningstype og belastningskategori, mens Damforskriftene og NS’3472 anvender begrepene låstkoeffisient γf og materialkoeffisient γm. Her blir sikkerhetsfaktoren: ks = γf γm
Damforskriftenes hovedregelen er γf lik 1,2. For innstøpte platekasser reduseres γf til 1,1. Redusert lastkoeffisient tillates også ved dimensjonering med ulykkesbelastninger og belastninger som følge av krigshandlinger. Da settes γf lik 1,0. Lastkoeffisient 1,0 benyttes dessuten for krefter som i kombinasjon med andre krefter virker gunstig. En diskuterbar regel gjelder kontroll av utmattingsgrensetilstand. Her tillates det at utmattingsberegning sløyfes hvis γf ved statisk beregning settes lik 1,4.
Materialkoeffisienten γm skal etter hovedregelen være 1,4, men kan reduseres til 1,2 for innstøpte platekasser. Ved beregninger med ulykkesbelastning eller belastning som følge av krigshandling tillates 1,1.
Damforskriftenes henvisning til DIN 19704 som beregningsstandard kan muligens tolkes dit hen at en beregning utført iht. den tyske norm med de sikkerhetsfaktorer som her gis, vil bli godkjent av NVE.
5.3 TBK og Rules for Certification of Diving Systems
Ved dimensjonering av kraftverksrør for innvendig overtrykk har det vært vanlig å legge TBK til grunn. Denne og RCDS har det til felles at de for positive membranspenninger (strekkspenninger) angir en tillatt spenning som skal være minste verdi av σ0,2/ks1 og σb/ks2.
| TBK: | Generelt: | ks1=1,5 | ks2=2,4 |
| RCDS: | Ferrittiske/martensittiske stål: | ks1=1,8 | ks2=2,7 |
| RCDS: | Austenittiske stål: | ks1=1,5 | ks2=2,7 |
| RCDS: | Aluminiumslegeringer: | ks1=1,5 | ks2=4 |
For knekking av skallkonstruksjoner med utvendig overtrykk, angir RCDS en sikkerhetsfaktor sammensatt av 4 ulike koeffisienter:
Lastkoeffisient : γ = 1,1 - 1,3 (Trykkavhengig)
Materialkoeffisient: γm = 1,15 (For stål)
Geometrikoeffisient: Ψ = 0,75 - 0,9 (Avhengig av skalltype)
Geometrikoeffisient: κ = 1,0 - 1,3 (Avhengig av slankhet λ)
Resulterende sikkerhetsfaktor blir k = γ•γm•κ/Ψ, og har tallverdi mellom grensene 1,41 og 2,52.
5.4 “Finite elements”-beregning
Sikkerhetsfaktorene foran er fastlagt med tanke på globale spenninger slik disse fremkommer ved vanlige beregningsformler. I de senere år har beregninger med “finite elements” fått utbredelse. Et problem blir da at det avdekkes lokale spenningsspisser som ikke fremkommer ved konvensjonelle beregninger. Eksempelvis blir lokale spenningsspisser ved et hull i en plate 3 ganger større enn global spenning.
Hvordan disse skal vurderes ift. beregningsstandardenes tillatte spenningsnivåer, er det i dag ikke omforente regler for. Undertegnede er av den oppfatning at man i hvert enkelt tilfelle må vurdere alle usikkerheter som inngår i dimensjoneringsanalysen. Til støtte ved dette kan man eksempelvis benytte [16] hvor sikkerhetsfaktoren i kapittel 4.9 presenteres som en usikkerhetsfaktor sammensatt av ulike bidrag. Her må man imidlertid også være klar over at mens [16] forutsetter at de ulike usikkerheter settes sammen ut fra sannsynlighetsbetrakting av ekstremalverdiers samtidige opptreden, taler “Damforskriftenes ånd” for at det er den direkte sum av ekstremalverdier som skal benyttes.
Finner man ved en “finite elements”-beregning uakseptable spenningsspisser, blir det viktig at også beregningen vurderes. Det hender at “uakseptabel” spenning skyldes uheldig elementinndeling og har således lite å gjøre med virkelighet.
5.5 Avledete størrelser
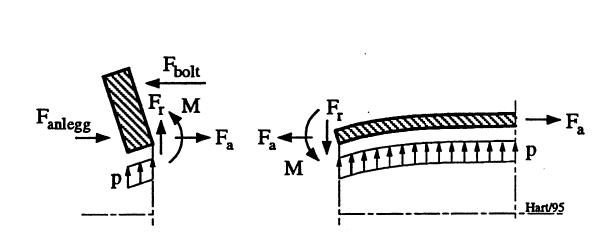
I noen tilfeller kan det være grunn til å spørre om det skal regnes “lastfaktor på lastfaktor”. Problemet oppstår fordi lastfaktoren slik den fremkommer i Damforskriftene, ikke entydig angir usikkerhet for belastning, men inngår som generelt bidrag til resulterende sikkerhetsfaktor. Som illustrasjon av dette kan man se på et strekkstag skjøtet med lasker og bolter som vist i Figur 2.
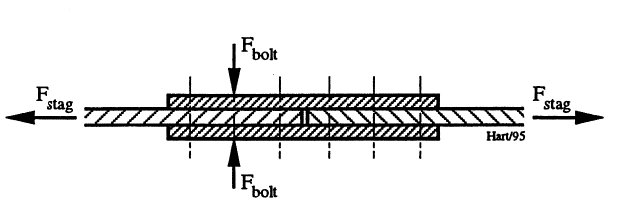
Kraften Fstag forutsettes overført ved friksjon fra den ene stagdel til den andre via viste lasker. Friksjonskreftene fremskaffes ved forspenning av de seks boltene som det er inn- tegnet senterlinjer for i laskeskjøtens halvdeler. Med friksjonskoeffisient μ må Fbolt. være større enn: μ • Fstag / 6.
Tenker en seg at strekkstaget bærer vekten av et konstruksjonselement, blir Fstag multiplisert med lastfaktor (1,2). I tillegg må det i ulikheten benyttes minste forventede verdi av μ (eks.: 0,7 • μtabell) samtidig som det bør være en viss overkapasitet for boltkraften (eks.: 1,2). Forspenning av boltene med momentnøkkel, medfører dessuten også usikkerhet, som regel ± 30 %. Nominell tilsetting ved denne type forspenningsregistrering må derfor settes slik at man med rimelig sikkerhet får den nødvendige boltkraft. Det kan derfor bli aktuelt å multiplisere sistnevnte med faktor 1,3 for å få nominell boltkraft.
Ved fasthetskontroll av boltene bør man imidlertid forholde seg til det nominelle tilsettingsmomentet, tillegge aktuell usikkerhet for boltkraften (1,3) og multiplisere med lastfaktor (1,2). Ift. teoretisk beregning uten justering for usikkerhet og lastfaktorer får man med de antydete enkelt-faktorer en resulterende faktor på nærmere 4,2.
Tankegang som angitt foran benyttes ikke i en beregningsstandard som TBK. Her anbefales det riktignok at boltforspenning kontrolleres ved måling av forlengelse. Hvordan man med dette kommer ut med usikkerhet ift. det forannevnte, er noe som vil variere fra et design til et annet.
5.6 Eksempel: Vannlast
For en damluke er midlere dybde ift. HRV 98 m. Vanntrykkbelastet flate er 6,80 m2. Damforskriftene krever lastfaktor 1,2. Dim. vannlast:
\[F = \gamma _f \cdot \rho \cdot g \cdot h \cdot A = 1,2 \cdot 1000 \cdot 9,81 \cdot 98 \cdot 6,8 = \text{7 885 000 N}\qquad{(1)}\]
Kommentar: Dimensjonerende vannlast skal være største last som kan forekomme. Samtidig er imidlertid h meget nær det maksimalt opptredende trykk som inntreffer ved PMF (påregnelig maksimalflom). Påslag med 20 % som γf innebærer, kan derfor her ikke begrunnes ut fra objektiv vurdering av belastningsusikkerhet.
5.7 Eksempel: Dimensjonerende spenning
Et lukeblad skal produseres av lavlegert stål med σF = 230 MPa. Iht. Damforskriftenes tilhørende regler settes materialfaktoren til 1,4. Dimensjonerende spenning som beregnede spenninger skal sammenlignes med, kan man finne til:
\[\sigma _d = \sigma _F/\gamma _m = 230 / 1,4 = 164 MPa\qquad{(2)}\]
6 Krefter og belastninger
6.1 Belastningstyper
Ved dimensjoneringsoppgaver må man innledningsvis bestemme aktuelle krefter. Disse kan være av ulik type, gruppert som angitt nedenfor:
Hydrostatiske krefter.
Hydrodynamiske krefter.
Friksjonskrefter.
Krefter pga. istrykk.
Aksellerasjons- og retardasjonskrefter.
Krefter pga. temperaturvariasjoner.
Krefter pga. egenvekt.
Trafikkbelastninger.
Krefter som inngår i analyser av brudd- eller ulykkesgrensetilstand, skal iht. Damforskriftenes regler være multiplisert med lastfaktor som angitt i Kapittel 5. For krefter som inngår i beregninger for utmattingsgrensetilstand og bruksgrensetilstand, er derimot reglene diffuse. Når det gjelder lastfaktor for bruksgrensetilstanden, kommer en tilbake til denne i Kapittel 17.
Hydrostatiske og hydrodynamiske krefter omtales i manuskriptet “Strømningsteknikk i kraftverksvannvei”. Spesielle belastningsforhold får man imidlertid for innstøpte konstruksjoner som platekasser og rør. Belastningene inndeles her i driftsbelastninger og belastninger ved montasje, innstøping og injeksjon.
6.2 Belastninger for innstøpt platekasse
For driftsbelastning på platekasser stiller Damforskriftene intet krav om dimensjonering for innvendig overtrykk. Derimot spesifiseres det kontroll mot innbuling pga. utvendig overtrykk:
Oppstrøms platekasse: Trykkforskjellen fra utside til innside settes lik innvendig hastighetshøyde.
Nedstrøms platekasse: Trykkforskjellen fra utside til innside settes ved luken lik det dimensjonerende trykk. Herfra avtar trykkforskjellen lineært til 1/3 ved platekassens nedstrøms ende.
Det skal tas hensyn til belastningene ved støping og injeksjon.
For innstøpingskreftene anbefaler undertegnede at verdiene nedenfor legges til grunn. Damforskriftene krever i tillegg lastfaktor γf = 1,1.
- Støpetrykk under platekasse: 100 kPa
- Opptrykk regnet under hele bunnen: 25 kPa
- Sidekraft på grunn av skjev støping: 6000 N/m (lengde)
- Støpetrykk mot overside medstivnet betong under platekassen: 25 kPa
- Injeksjonstrykk mot plater: 300 kPa
I spesielle tilfeller med korte platekasser eller sirkulære rørpansringer som tåler høye utvendige overtrykk, bør det vurderes å tillate at injeksjonstrykket mot konstruksjonen økes til det trykk som benyttes ved injeksjonen i betongproppen og mellom denne og fjellet. Dette er vanligvis lik det maksimale fremtidige vanntrykk.
Vedr. belastning på innstøpte konstruksjoner pga. innvendig vanntrykk, er det vanlig at man for platekasser ser bort fra dette. Det forutsettes da at kreftene overføres til betong og opptas i denne eller videreføres til fjell. Her bør imidlertid forutsetningene være gjennomtenkt. En tynn betongplate med vanlig svinnarmering påstøpt en platekasses side, rettferdiggjør eksempelvis ikke betegnelsen “innstøpt platekasse” uten at betongplaten er i stand til å oppta kreftene fra platekassens innvendige trykk.
6.3 Innstøpte rør
Innstøpte rør er ikke underlagt Tilsynsforskriften. Et unntak er dog hvis det innstøpte rør er oppstrøms pansring for en tverrslagsport. Damforskriftene kommer dessuten til anvendelse hvis et innstøpt rør er montert i en dam. Ut over generelle krav til bygningskonstruksjoner er en anleggseier ikke pålagt noe regelverk for belastningsfastsettelse. Reglene som antydes i det etterfølgende blir derfor å anse som bransjepraksis og har sitt opphav i beregningsprosedyrer fra en tid før lastfaktoren var “oppfunnet”. Av denne grunn benyttes det ikke lastfaktor ved beregning av innstøpte rør. Nevnte konstruksjoner blir dessuten dimensjonert for innvendig trykk. Forskjellen i beregningsforutsetninger som man følgelig har mellom innstøpte rør og platekasser, kan synes ulogisk.
For innstøpte rør forutsettes det at det innvendige vanntrykk i helhet balanseres av tangensialspenningene i rørveggen. Enkelte forsøk indikerer at det kan være 25 - 50 % av kreftene som videreføres til fjell. Fordi spenningstilstanden i et fjellmassiv ikke er isotrop, blir imidlertid denne kraftoverføringen meget kompleks og kan i utgangspunktet ikke forutsettes konstant rundt omkretsen.
Som dimensjonerende innvendig overtrykk benyttes det enkelte tverrsnitt maksimale statiske vanntrykk tillagt dynamisk trykkøkning ved ugunstigste aktuelle retardasjon av vannstrømmen. Lastfaktor benyttes ikke. Man tar heller ikke eventuelle utvendige poretrykk med ved fastleggelsen av det resulterende innvendig dimensjonerende overtrykk.
Ved dimensjonering av innstøpte rør med store tverrsnitt kan innknekking som følge av utvendig poretrykk ved tømt rør, bli vel så viktig som det innvendige overtrykket. For fastleggelsen av nevnte poretrykk har det vært ulik praksis. De mest vanlige regler har vært å sette utvendig trykk lik maksimalt statisk innvendig trykk, lik vertikal avstand opp til fri fjelloverflate eller lik vertikalkomponenten for perpendikulæren ut til den frie fjelloverflaten. Seriøs prosedyre tilsier dog at dimensjonerende utvendig overtrykk vurderes av kvalifisert ingeniørgeolog.
6.4 Frittliggende rør
Rapporten “Kraftverksrør. Prosjektering, drift og vedlikehold” [3] gir god oversikt vedr. krefter som det ved denne type konstruksjoner må tas hensyn til. I tillegg kan det også vises til NVEs “Retningslinjer for glassfiberarmerte kraftverksrør”.
6.5 Friksjonskrefter
For ulike materialkombinasjoner spesifiserer Damforskriftenes regler friksjonskoeffisienter, se referert liste i det etterfølgende. Dette er maksimalverdier man skal benytte ved fastleggelse av manøvreringskapasitet. Dimensjoneres derimot friksjonsforbindelser, blir det minimumsverdier som må benyttes. Disse får selvsagt lavere verdi enn de foran- nevnte.
Rullemotstand Frulle, bestemmes som vist i Figur 3 ved hjelp av f, se neste side.
Når det gjelder friksjonskoeffisientene som refereres fra Damforskriftenes regler, kan det påpekes at det tidligere, før 60-tallet, var vanlig å regne friksjonskoeffisient 0,4 for stål mot bronse/messing. Dette innebærer at mange luker nå, ut fra dagens krav, har underdimensjonerte manøvreringsinnretninger. Nevnes kan det også at målinger utført på eldre luker viser at 0,6 faktisk blir en realistisk friksjonskoeffisient.
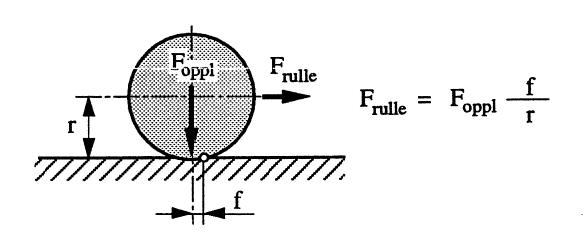
Glideluke: Usmurt glidelist av bronse/messing mot stål: μ = 0,6
Rulleluke: Usmurte bronselager: μ = 02
Rulleluke: Spesialglidelager: μ = ned til 0,15
Rulleluke: Rullemotstand: f = 0,05 mm
Pakninger: Gummi, neopren, etc. mot stål: μ = 0,7-0,9
Selv om glidelister med spesielle lavfriksjonsbelegg anvendes, frarådes det at det for glideluker nyttes vesentlig lavere friksjonskoeffisient enn angitt foran. I den senere tid har det vært utspill med tanke på å benytte reduserte friksjonskoeffisientene ifm. spesielle materialvalg. Dette har sammenheng med at redusert friksjonskoeffisient minsker spillkapasitetsbehovet. Faktum er dog at langtidserfaring med de aktuelle materialkombinasjonene mangler. Et av de aktuelle spørsmål er om fremmedpartikler etter års bruk kan bake seg inn i myke flater og ved dette øke friksjonen.
6.6 Istrykk
Istrykk oppstår når is utvider seg pga. temperaturstigning. Kraften varierer med istykkelse og beskaffenhet. “Forskrifter for dammer” oppgir i avsnitt 6.5.3 at istrykket har størst verdi ved 50 cm istykkelse, men at trykket reduseres hvis isen ved utvidelse får anledning til å gli opp langs slak damskråning eller svakt stigende strand.
Damforskriftenes generelle krav er at istrykket i hvert enkelt tilfelle skal vurderes med kompetent ekspertise. En vanlig fastsettelse av islasten blir imidlertid 100 kN/m og at den forutsettes å angripe 0,25 meter under HRV.
6.7 Temperaturvariasjoner og temperaturkrefter
For fastsettelse av krefter som følge av temperaturvariasjoner, kan det vises til DIN 19704. Retningslinjer for hvilke temperaturvariasjoner som bør påregnes, blir iht. denne norm:
Konstruksjoner som konstant eller tidvis ligger helt eller for størstedelen over vannivået, + 35 °C.
Konstruksjoner som konstant eller tidvis kun med en mindre del ligger over vannivået eller som er beskyttet mot større temperaturvariasjoner, + 20 °C.
Konstruksjoner som er konstant dykket, + 10 °C.
Temperaturvariasjonene blir dernest å omregne til deformasjon. I følge DIN 19704 skal den lineære temperaturutvidelseskoeffisienten for dette settes til αstål = 1,2•10-5 °C-1. Fastholdes en konstruksjon slik at temperaturdeformasjonen hindres, kan materialspenninger og temperaturkrefter beregnes vha. materialets elastisitetsmodul E.
6.8 Trafikkbelastninger
Vedr. trafikkbelastninger viser Damforskriftene i punkt 6.7 til lastforskrifter i veinormalene fra Statens Vegvesen. I tillegg til dette bør man dimensjonere trinn og gangbaner iht. DIN 19704 med flatebelastning 2500 Pa. Det kan også være aktuelt å kreve at deler av en konstruksjon hvor personer kan stå eller klatre, må tåle minst 1000 N plassert som punktlast på ugunstigste sted.
6.9 Krefter i fagverk
Enkelte eldre lukekonstruksjoner er utført med fagverk. Skal disse revurderes, kan beregningsarbeidet bli omfattende hvis opprinnelige beregninger ikke er tilgjengelige og stagkreftene må fastlegges og analyseres på nytt.
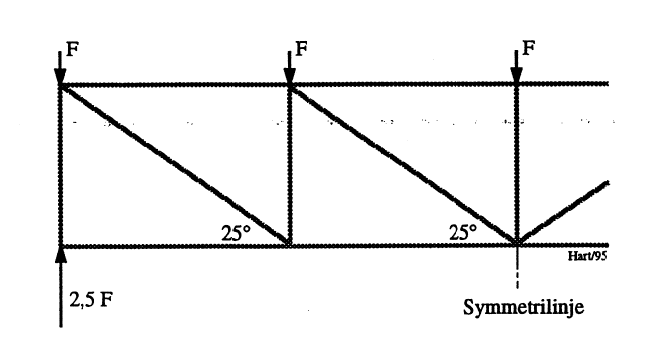
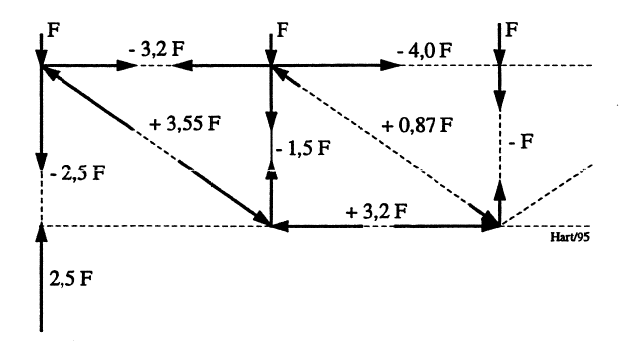
En oversiktlig metode som reduserer muligheten for at man “går seg vill” i fagverket, er den grafiske. Da tegnes fagverket opp i egnet målestokk og påføres aktuelle belastninger. Metoden illustreres i Figur 4 og Figur 5. Ytre belastninger angis i førstnevnte, mens Figur 5 også inneholder stavkrefter. For det enkelte knutepunkt kan man kontrollere kraftbalansene visuelt ved måling av vektorer. Vanlig tilnærming er at alle knutepunkter betraktes leddet og at de følgelig ikke overfører bøyemomenter.
7 Strekk- og trykkspenning
7.1 Normalspenning
Normalspenning er kraft overført gjennom et enhetstverrsnitt som ligger perpendikulært kraftretningen. Strekk- og trykkspenninger kan begge oppfattes som normalspenninger. Blir en strekkstav med tverrsnitt A utsatt for strekk F, blir strekkspenningen:
\[\sigma = F / A\qquad{(3)}\]
7.2 Flatetrykk for glidelister
Flatetrykket på glidelukers glidelister beregnes ved: p = F/ A. Med bronse mot rustfritt stål har det vært vanlig å sette maksimalt tillatt flatetrykk til 10 MPa. Lastfaktor 1,2 forutsettes da innregnet. En ser imidlertid bort fra kantpress og regner kraften jevnt fordelt på den belastete flate.
Det er grunn til å påpeke at usmurte opplagringsflater hvor det blir bevegelse mellom flatene, bør ha ulike hardheter. For dette blir det vanligvis anbefalt en forskjell på minst 50 HB.
7.3 Hjultrykk
Hertz-spenning beregnes for rullelukers opplagringer. Har hjul og skinne samme elastisitetsmodul E, blir:
\[\text{Hertz-spenning:} \space\space \sigma _{HE} = 0,42 \cdot (F \cdot E / (B \cdot r ))^{0,5}\qquad{(4)}\]
\[\text{Damforskriftenes krav:} \space\space \sigma _{HE} < 1,4 \cdot \sigma _B\qquad{(5)}\]
B og r er henholdsvis hjulbanens bredde og radius. Strekkgrensen σB gjelder forbindelsens svakeste materiale.
Formlene har vært benyttet ved hjultrykk opp mot 1000 KN. For høytrykks nødstengeluker med hjultrykk opp mot 2000 kN, er mer avanserte beregningsmodeller tatt i bruk.
Ved fastleggelsen av hjultrykk er det et vesentlig at kreftene fra lukebladet fordeles til hjulene som forutsatt. Dette kan nødvendiggjøre presisjonsmaskinering av hjulinnfestninger og føringer eller at lukebladet oppdeles i boggier.
7.4 Flatetrykk mot betong
Grense for maksimalt flatetrykk fra ståldeler, mot standardbetong er 10 MPa. I dette blir lastfaktor 1,2 innregnet.
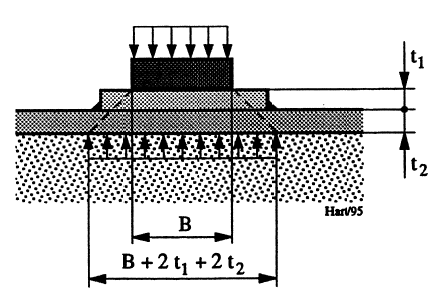
Føres kreftene gjennom lister og stålplater er det vanlig å fordele lasten utover med vinkel 45°, se Figur 6.
Økes betongens fasthet ut over det vanlige, tåler den selvsagt også større flatetrykk enn forannevnte 10 MPa. Flatetrykket kan likeledes økes hvis betongen er godt understøttet sideveis.
7.5 Membranspenninger i sfæriske og sylindriske skall
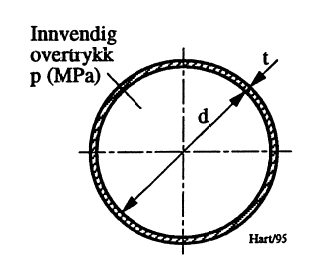
Ved kuleskall og tynnvegget rør utsatt for innvendig overtrykk som vist i Figur 7, kan ligninger for membranspenninger lett utledes.
\[ \text{Kulespenning:} \sigma = p \cdot d /(4 \cdot t)\qquad{(6)}\]
\[ \text{Sylinderspenning tangensielt:} \sigma _t = p \cdot d / (2 \cdot t) \qquad{(7)}\]
\[ \text{Sylinderspenning aksielt:} \sigma _a = p \cdot d / (4 \cdot t) = \sigma _t / 2\qquad{(8)}\]
Angitte aksialspenning opptrer i sylindervegg hvis røråpningen er tett. Kulespenningen blir selvsagt lik i alle skallretninger.
For både sfæriske og sylindriske skall avhenger spenningsangivelsen foran av at virkelig geometri overenstemmer med den teoretiske. Avvik som oppstår ved sveising, dårlig tilpassing, etc., kan gi betydelige tilleggsspenninger. Formlene gjelder heller ikke når sylindriske rørlengder skjøtes slik at røraksene danner vinkel med hverandre.
7.6 Eksempel: Aksialspenning i gjenget bolt
En bolt M16 utsettes for 25 000 N strekk. Gjengene har kjernetverrsnitt 141 mm2. Bolt- spenning referert til kjernetverrsnitt blir:
\[\text{Boltspenning:}\space\space\space \sigma = F / A = 25000 / 141 = 177 MPa\qquad{(9)}\]
Spenningen er beregnet ut fra kjernetverrsnittet. Vanlig er det også å benytte spennings- tverrsnittet. Data for spenningstverrsnitt referert til ulike gjengetyper og dimensjoner fremgår av [16]: For M16 blir eksempelvis dette 157 mm2.
7.7 Eksempel: Membranspenninger i rør
Et rør DN 200 med veggtykkelse 5 mm har 12 bar innvendig overtrykk (inkludert last- faktor). Rør-enden er stengt med ventil. Det regnes I mm rustfradrag på både innvendig og utvendig flate.
\[ \text{Vanntrykk:}\space\space p = 12 \space \text{bar} = 12 \cdot 10^5 \space \text{Pa} = 1,2 \space \text{MPa} \qquad{(10)}\]
\[ \text{Tangensialspenning:}\space\space \sigma _t = p \cdot d / (2 \cdot t) = 1,2 \cdot 200 / (2\cdot(5-2)) = 40 \space \text{MPa} \qquad{(11)}\]
\[ \text{Aksialspenning:}\space\space \sigma _a = \sigma _t/2 = 33/2 = 20 \space \text{MPa} \qquad{(12)}\]
8 Enakset bøyespenning
8.1 Bøyebelastning for bjelke
Bøyespenning oppstår når stav eller bjelke utsettes for et bøyemoment M. Forholdet illustreres i Figur 8 hvor en utkraget bjelke er belastet med kraft F.
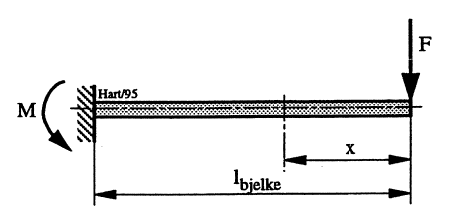
Langs bjelken er bøyemomentet gitt ved produktet F•x. Dette får maksimal størrelse ved innfestingen til venstre. Har bjelken motstandsmoment W, gis maksimal bøyespenning ved:
\[\sigma _{max} = M_{max} / W = F \cdot x_{max} / W = F \cdot l_{bjelke} / W\qquad{(13)}\]
Formler for bøyemomentets variasjon langs bjelker avhengig av belastning og opplagringsbetingelser gis i en rekke håndbøker. Av slike angis [14], [6] og [5] i Litteraturreferanser. I de samme håndbøker vil man finne tverrsnittsdata med bl.a. motstandsmoment W. En må imidlertid være oppmerksom på at disse ikke er korrigert mhp. rustfradrag.
Belastningen på forannevnte bjelke medfører at bjelken får trykkspenninger i underkant og strekkspenninger i overkant. Mellom over- og underkant endres bøyespenningen lineært. Dette er avhengig av at materialet oppfører seg iht. Hooks lov, dvs. har konstant elastisitetsmodul E. Forangitte bøyespenningsformel gjelder således ikke for grått støpejern.
8.2 Plate opplagret på bjelker
Plane lukeblad hvor frontplaten ligger opplagret på horisontale støttebjelker, kan regnes som en bjelke som spenner fra støttebjelke til støttebjelke. I praksis er riktignok platen et platefelt opplagret langs alle 4 sidekanter. Den todimensjonale spenningstilstanden som ved dette oppstår, er nærmere belyst i neste kapittel. Er imidlertid den ene sidekanten mer enn dobbelt så stor som den andre, blir likevel platefeltbetraktningen mindre nødvendig. Da er det endimensjonal “bjelkeeffekt” som dominerer.
8.3
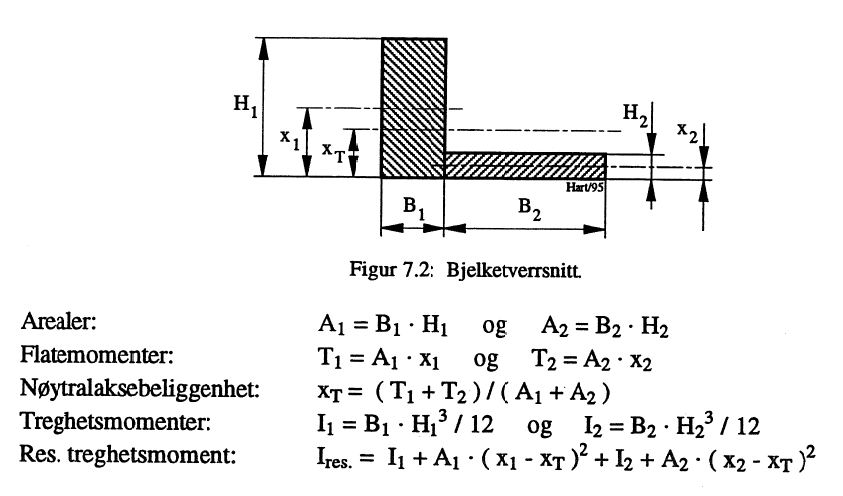
Har man å gjøre med ikke-symmetriske bjelketverrsnitt, kan det ved beregning være praktisk å benytte treghetsmomentet I i stedet for motstandsmomentet W. Ved fastleggelse av treghetsmoment benytter man seg ofte av at dette for et rektangulært profil med høyde H og bredde B er I rek = B • H3 / 12. Tilsvarende størrelse for sirkulært tverrsnitt blir Isirk = π • d4 / 64.
Fastleggelsen av treghetsmomentet for et tverrsnitt som vist i Figur 9 begynner med bestemmelse av profilets nøytralakse. Avstanden denne har fra profilets grunnlinje utregnes som forholdet mellom flatemomentet om grunnlinjen og profilets areal. Dernest beregnes treghetsmomentene for tverrsnittets enkeltdeler. Beregningen avsluttes med fastleggelse av resulterende treghetsmoment vha. Steiners sats.
8.4 Eksempel: Spenninger i frontplate på tvers av bjelkeretning
Frontplaten for et lukeblad er sveist til oppstrøms kant av plateribber med senteravstand 400 mm. Frontplaten har tykkelse 25 mm. Dimensjonerende vanntrykk, inkl. lastfaktor, er 0,74 MPa = 0,74 Nmm2.
Fordi frontplatebelastningen er tilnærmet symmetrisk om ribbene, blir vinkeldeformasjonen her lik null. Platen anses derfor som 2-sidig fast innspent bjelke med enhetsbredde 1 mm, lengde 400 mm og belastning q = 0,72 N/mm. Det forutsettes I mm rustfradrag på hver side.
\[ \text{Maks. moment iht. håndbok:}\space\space M = q \cdot l_{bjelke}^2 / 12 = 0,72 \cdot 400^2 / 12 = 9600 \space\text{Nmm}\qquad{(14)}\]
\[ \text{Treghetsmomenit:}\space\space W = B \cdot H^2 / 6 = 1 \cdot (25 - 2)^2 / 6 = 88,2 mm^3 \qquad{(15)}\]
\[ \text{Maksimal bøyespenning:}\space\space \sigma = M/W = 9600 / 88,2 = 109 MPa \qquad{(16)}\]
8.5
En bjelke har tverrsnitt som vist i Figur 10. Dimerisjonene er inkludert rustfradrag. Maksimalt bøyemoment om angitt nøytralakse har blitt bestemt til 36 000 kNm.
Profilets areal:
\[ A_1 = B \cdot t_1 = 220 \cdot 14 = 3080 \space \text{mm}^2 \qquad{(17)}\]
\[ A_2 = t_2 \cdot (H-t_1) = 12 \cdot (285-14) = 3252 \space \text{mm}^2 \qquad{(18)}\]
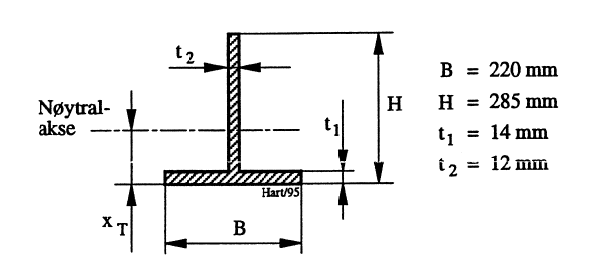
Nøytralaksens beliggenhet:
\[ x_T = (A_1 \cdot t_1 / 2 + A_2 \cdot (H + t_1)/2)/(A_1+A_2) \qquad{(19)}\]
\[ \space \space \space \space \space = (3080\cdot 7 + 3252\cdot 299/2)/(3080+3252) \qquad{(20)}\]
\[ = 80 \text{mm} \qquad{(21)}\]
Treghetsmomenter:
\[ I_1 = B \cdot t_1^3 / 12 = 220 \cdot 14^3 /12 = \text{50 000} \space\text{mm}^4 \qquad{(22)}\]
\[ I_2 = t_2 \cdot (H - t_1)^3 / 12 = 12 \cdot (285 - 14)^3 / 12 \qquad{(23)}\]
\[ = \text{19 900 000 mm}^4 \qquad{(24)}\]
Resulterende treghetsmoment iht. Steiners sats:
\[ I_{res} = I_1 + A_1 \cdot (x_T - (t_1/2))^2 + I_2 + A_2 \cdot (((H+t_1)/2)-x_T)^2 \qquad{(25)}\]
\[ = 50000 + 3080 \cdot (80 - 7)^2 + 19900000 + 3252 \cdot (((285+14)/2) - 80)^2 \qquad{(26)}\]
\[ = 50000 + 16413000 + 19900000 + 15708000 = \text{52 100 000 mm}^4 \qquad{(27)}\]
Med angitt bøyemoment M er bøyespenningene øverst og nedert henholdsvis:
\[ \sigma _ø = (M/I)\cdot (H-x_T) = (36 000 000 / 52 100 000 ) \cdot (285 - 80) = 142 \space \text{MPa} \qquad{(28)}\]
\[ \sigma _n = (M/I)\cdot x_T = (36 000 000 / 52 100 000 ) \cdot 80 = 55 \space \text{MPa} \qquad{(29)}\]
9 Toakset bøyespenning i plate
9.1 Generelt
Ifm. toakset spenningstilstand i plater kan to strukturelementer fremheves, dels fordi de går igjen i mange vannkraftkonstruksjoner, dels fordi fasthetsberegningene forenkles ved bruk av ferdige algoritmer. Elementene er:
Rektangulære plater med jevnt fordelt belastning, opplagret langs sidekantene.
Plane rotasjonssymmetriske plater med rotasjonssymmetrisk belastning og opplagring
Førstnevnte element kan være i lukebladet for rulle- og glideluker hvor en plan rektangulær plate ligger fastsveist på et ribbesystem. Spenningssituasjonen for slik plate er også omtalt i kapittel 6 fordi man ofte kan betrakte platen som bjelke med enakset spenningstilstand. Ønsker man derimot å vurdere tilfellet som 2-akset spenningstilstand, blir ferdige ligningsløsninger bl.a. å finne i DIN 19704 [4] og i Hitte [6]. For den som søker det teoretiske grunnlaget for slik beregning, kan dessuten [13] anbefales. Alle nevnte referanser er i Kapittel 18.
9.2 Rektangulære platefelt
En aktuell opplagringssituasjon for rektangulære plater med jevnt fordelt belastning er fast innspenning langs alle sider. Dette kan vurderes som faktisk situasjon når planten er sveist til et stivt bjelkesystem. Figur 8.1 viser en plate av nevnte type hvor sidekant a er mindre eller lik sidekant b. Her identifiseres materialspenningene ift. plategeometrien.
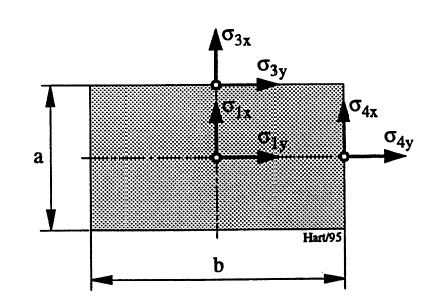
I følge [4] gis spenningene i den aktuelle platen ved formlene nedenfor. Her er p (MPa) midlere vanntrykk mot platen og t platetykkelsen.
\[ \sigma = \phi \cdot p \cdot (a/t)^2 \qquad{(30)}\]
Konstanten φ for de ulike spenningene finnes som funksjon av forholdet b/a i etterfølgende tabell. Tilsvarende tabeller for andre innspenningsbetingelser fremgår av håndbøker.
| b/a | σ1x | σ1y | σ3x | σ3y | σ4x | σ4y |
|---|---|---|---|---|---|---|
| >>3 3,0 2,0 1,5 1,0 | 0,250 0,250 0,247 0,221 0,137 | 0,075 0,075 0,095 0,122 0,137 | 0,500 0,500 0,499 0,455 0,309 | 0,150 0,150 0,150 0,137 0,093 | 0,103 0,103 0,103 0,103 0,093 | 0,342 0,343 0,343 0,343 0,309 |
9.3 Rondeller og ringplater
Som eksempel på rotasjonssymmetrisk platedeler, kan man tenke seg et blindlokk. Vanlig forenkling er å forutsette rotasjonssymmetrisk momentfri opplagring ved boltenes delesirkel og jevnt fordelt trykk ut til denne. Belastningssituasjonen blir da som avbildet i Figur 12.
I likhet med tilfellet “rektangulær plate” får man bøyemomenter i to retninger, her radielt og tangensielt. Dette gir 2-akset spenningstilstand. Består problemet i å finne spenningenes maksimalverdier, lar dette seg enkelt gjøre vha. formler fra eldre utgave av [5]. Grunnformelen tilsvarer det uttrykk man hadde for rektangulær plate. Verdier for faktoren φ ved jevnt fordelt flatetrykk gis i det etterfølgende for både momentfri opplagring langs omkretsen (som vist i Figur 12) og fast innspenning.
| Spenning: | σ = φ•p•(r/t)2 | ||
| Fritt opplagret: | Plateperiferi (x=r): Platesenter (x=0): | φradiell = 0,00 φradiell = 1,24 | φtangensiell = 0,53 φtangensiell = 1,24 |
| Fast innspent: | Plateperiferi (x=r): Platesenter (x=0): | φradiell = -0,75 φradiell = 0,49 | φtangensiell = -0,23 φtangensiell = 0,49 |
Er det nødvendig å fastlegge spenningene ved andre verdier av x, finnes nødvendige formler for dette i bl.a. [6]. Setter man inn i disse ν = 0,3, W = t2/6 og x henholdsvis 0 og r får man verdiene som foran angis for φ.
9.4 Eksempel: Rørflens regnet som ringplate
En flensforbindelse er vist i Figur 13. For denne skal en se nærmere på løsflensen. Som beregningsanalogi forutsettes det en ringplate med innvendig og utvendig diameter henholdsvis Ø300 og Ø450 mm. Belastningen fra boltene ytterst og ringopplagringen innerst er jevnt fordelt langs omkretsene. Belastningsbildet gjør at det radielle moment innerst og ytterst blir: Mr = 0.
Aktuelle beregningsformler finnes i [6]. Som det fremgår av referansen får man maksimalt tangensialmoment innerst, dvs. ved Ø300. Moment er i referansen angitt som spesifikt moment regnet pr. lengdeenhet langs periferien. Forutsettes det Poissons tall 0,3 og forhold mellom ytre og indre diameter lik m = 450/300 = 1,5 kan momentet skrives som:
\[ M=(F/(4\pi))\cdot[ 1,3\cdot ln(m) + 1,3\cdot ((m^2+1)/(m^2-1))\cdot ln(m) + 0,7] \qquad{(31)}\]
\[ = (100000 / (4\pi))\cdot [ 1,3\cdot ln(1,5) + 1,3\cdot((1,5^2+1)/(1,5^2-1))\cdot ln(1,5) + 0,7] \qquad{(32)}\]
\[ = 7958 \cdot [0,5271 + 1,3705 + 0,7000 ] = \text{20 670 Nmm/mm} \qquad{(33)}\]
\[ \text{Motstandsmoment:}\space\space W = t^2/6 = 60^2/6 = 600 \space \text{mm}^3\text{/mm} \qquad{(34)}\]
\[ \text{Bøyespenning:}\space\space \sigma = \text{M/W} = 20670 / 600 = 34 \space \text{MPa} \qquad{(35)}\]
Materialspenning blir lav. Beregning iht. beregningsstandarden TBK gir spenninger av samme størrelsesorden, men noe lavere, se Kapittel 10.2. Årsaken til dette er at man ovenfor har sett bort fra den del av flensen som ligger utenfor boltenes delesirkel.
Det er ellers verd å merke seg at spenningen i flensen ikke avhenger av det innvendige trykket i røret, men derimot av hvor meget flensboltene trekkes til.
10 Flensberegning
10.1 Generelt og flensberegning
Nøyaktige flensberegninger tar hensyn til interaksjonen mellom flens og rør. I tillegg inn- går alle krefter som systemet utsettes for. Avhengig av flensforbindelsens utforming kan dette inkludere: Boltkraft, kraft mot anleggsflate mot naboflens (med pakningstrykk), innvendig overtrykk i rørsystemet samt aksialbelastning. Prinsippet gjengis i Figur 14 hvor krefter og deformasjoner også er inntegnet.
Utledning av grunnlaget for slik beregning fremgår bl.a. av i Sølsnes, Maskindeler, bind 3. Det kan også nevnes at professor Sundby (den første professor ved Vannkraftlaboratoriet ved NTH) utga at hefte med tittel “Enkelte styrkeberegninger”. Dette var tidligere del av pensum for vannkraftstudenter.
Praktisk beregning av flensforbindelser bør imidlertid fortrinnsvis gjøres ved bruk av formler fra aktuelle beregningsstandarder. En av disse er TBK.
10.2 Beregning av løsflens
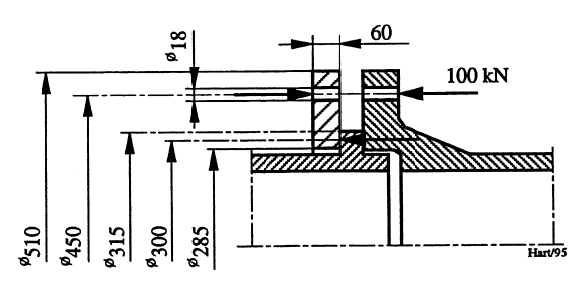
Flensen som ble beregnet i Kapittel 9.4 skal beregnes iht. TBK, avsnitt 19.3.1. Det benyttes symboler iht. TBK. Disse inngår ikke i symbol-listen foran.
Total skruekraft: Qs = 100 kN
Momentarm: w = 0,5•(Dh - (Di + 2•Dk)/3) = 0,5•(450 - (285 + 2•315)/3) = 72,5 mm
Moment: M = Qs•w = 100 000 • 75 = 7 500 000 Nmm
Bredde flensring: Bf = 0,5•(Df-Di) = 0,5•(510-285)= 112,55 mm
Konstant: Z = 1 - (db/(2•Bf)) = 1 - (18/(2•112,5))= 0,92
Spenning: Sti = 6/(π•Z•ln(Df/Di)) • (M/(hf2•Di)) = 6/(π•0,92•ln(510/285)) • (7,5•106 / (602•258)) = (6/1,6819) • (7,5•106/928 800) = 29 MPa
11 Skjærspenning pga. skjærkraft
11.1 Aktuelle formler
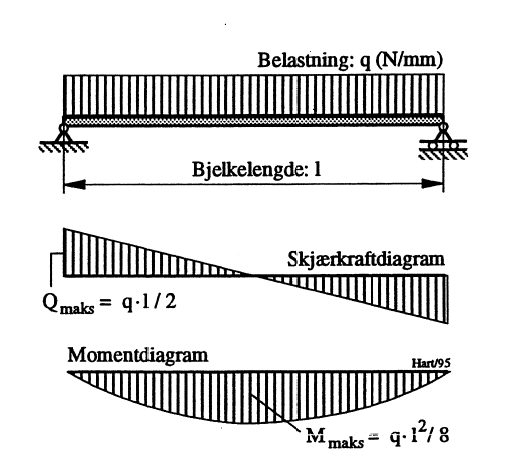
En bjelke vil avhengig av belastningen ha et gitt skjærspenningsdiagram. Ved tosidig fri opplagring og jevnt fordelt belastning blir dette som vist i Figur 15.
I figuren er q belastningen og Q skjærkraften. Belastningen gir skjærspenninger τ i alle tverrsnitt bortsett fra det midtre. Skjærspenningen har maksimal verdi ved tverrsnittets nøytralakse og er null ved profilets over- og underside. Der bøyespenningene har maksimalverdi, får således skjærspenningen minimalverdi. For rektangulære og sirkulære tverrsnitt blir maksimal skjærspenning henholdsvis:
τrektangulær = 1,5 • Q/A og τsirkulær= 1,33 • Q/A
I enkelte tilfeller har tverrsnittet slik form at skjærspenningene får høye verdier der bøye- spenningene samtidig er store. I slike tilfeller kan det være nødvendig å forta nøyaktig skjærspenningsbestemmelse. Da beregnes skjærspenningen med formelen:
Skjærspenning: t= Q•T/(I•b)
Her er: Q= skjærkraft. T=flatemoment for den del av tverrsnittet som ligger utenfor Skjærspenningssnittet, regnet ift. det totale tverrsnitts nøytralakse. I = det totale tverrsnitts treghetsmoment. b= bredden som skjærkraften virker over.
11.2 Skjærkraft ved nagle- og boltforbindelse
Forholdet foran medfører at det ved plater som er naglet til bjelker, vil bli skjærkrefter som må overføres gjennom nagleforbindelsen. Med nagleavstand lnagle kan skjærkraften som den enkelte nagle skal ta hånd om, utledes av skjærspenningsformelen i Kapittel 11.1:
Skjærkraft pr. nagle: Qnagle = Q • T • lnagle / I
11.3 Eksempel: Skjærspenning mellom bjelke og frontplate
Frontplaten for et lukeblad er sveist til oppstrøms flens på flensbjelke som vist i Figur 16. Maksimal skjærkraft Q er 187000 N. Angitte dimensjoner er korrigert mhp. rustfradrag. Skjærspenningen i sveisen skal beregnes. Fastleggelsen av tyngdepunktsaksens beliggenhet og treghetsmomentet blir som angitt i Kapittel 8.3.
Tverrsnittets areal medregnet rustfradrag: A = 15 084 mm2 Tyngepunktaksens beliggenhet: xT = 169 mm Treghetsmoment medregnet rustfradrag: I = 121,2•106 mm4
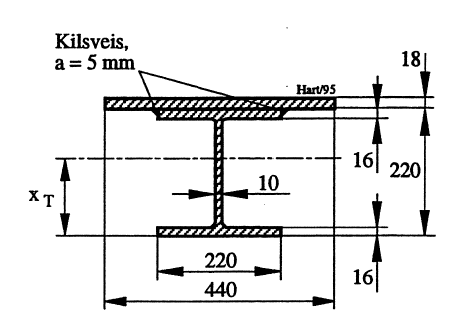
Skjærsp.:
\[\tau = Q\cdot T / (I\cdot b)\qquad{(36)}\] \[\space \space \space = (187000 \cdot (440 \cdot 16 \cdot (220-169)))/(121,2\cdot 10^6\cdot (2 \cdot 4))\qquad{(37)}\] \[\space \space \space = 69 \text{MPa}\qquad{(38)}\]
12 Vridningsspenning (torsjon)
12.1 Vridningsspenning i enkle profiler
Enkelte belastninger gir vridningsspenninger (torsjon). Et vanlig eksempel på dette har en ved drivaksler. På samme måte som maksimal bøyespenning i en bjelke kan finnes ved å dividere bøyemomentet med bjelkens motstandsmoment, kan vridningsspenningen finnes ved å dividere vridningsmomentet Mv med det polare motstandsmomentet Wp. For massiv og hul aksel med diameter d (ev. dy og di) og vridningsmoment Mv, blir vridningsspenningen konstant rundt omkretsen med tallverdi:
\[ \tau _{v, massiv} = M_{v} / W_p \space\space\space\space\text{hvor:} \space\space W_p = \pi \cdot d^3 / 16 \qquad{(39)}\]
\[ \tau _{v, hul} = M_{v} / W_p \space\space\space\space\text{hvor:} \space\space W_p = \pi \cdot (d_y ^4 - d_i ^4) / (16\cdot d_y)\qquad{(40)}\]
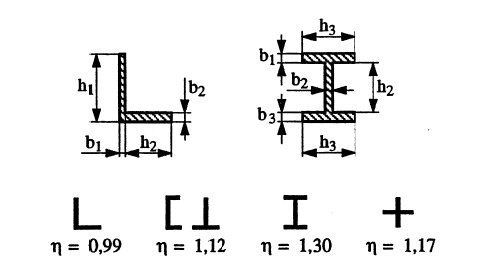
Ved firkantede tverrsnitt b x h med h/b >= 1, kan forholdet beregnes iht. [6]:
Vridningsspenning for kvadrat / rektangel:
\[ \tau _{v,maks} = \eta _2 \cdot M_v / (h \cdot b^2) = \tau _{vh}\qquad{(41)}\]
Største vridningsspenning opptrer ved overflaten på midten av lengste sidekant. Ved hjørnene er spenningen null og på midten av korteste sidekant-blir den: τvb = η1 • τvh. Størrelsene η1; og η2 gis ved:
| h/b= | 1,0 | 1,5 | 2,0 | 3,0 | 4,0 | 6,0 | 8,0 | 10,0 | >10 |
| η1= | 1,000 | 0,858 | 0,796 | 0,753 | 0,745 | 0,743 | 0,743 | 0,743 | 0,743 |
| η2= | 4,81 | 4,33 | 4,07 | 3,74 | 3,55 | 3,35 | 3,26 | 3,2 | 3,0 |
12.2 Vridningsspenning i lukkede tynnveggede tverrsnitt
For et tynnvegget, lukket tverrsnitt med frie ubelastede kanter og med platetykkelse t, blir fluksen τv•t [6]. Dette medfører at vridningsspenningen når A er omskrevet areal av tverrsnittplatenes senterlinje, kan uttrykkes ved den såkalte Bredtske formel som angir Wp = 2 • A • t.
Vridningspenning i lukket tynnvegget tv.snitt: τv = Mv/(2•A•t)
Sammenlignes uttrykket med formelen for ringtverrsnitt, ser en at overenstemmelsen blir best hvis A beregnes på grunnlag av ringtverrsnittets delediameter.
12.3 Vridningsspenning i åpne tynnveggede tverrsnitt
Dette gjelder bl.a. valsede profiler. I følge [5] blir her:
\[\tau _v = M_v / W_p \space\space\space\space \text{hvor:} \space\space W_p = \eta / (3\cdot b_{maks})\cdot \Sigma (b_i ^3 \cdot h_i)\qquad{(42)}\]
Definisjon av bi og hi samt angivelse av konstanten η fremgår av Figur 17. Det kan imidlertid bemerkes at enkelte andre kilder har avvikende verdier for η og at vridningsspenningene i hulkilene mellom de enkelte elementene kan bli 60 % større enn det som ved de her presenterte data fremkommer som største skjærspenning.
12.4 Vridningsspenning i mindre klappeluke
En klappeluke er konstruert med tykkvegget rør nederst, se Figur 18. Røret har utvendig diameter Ø350 mm og veggtykkelse 20 mm. Fra røret utkrages lukebladet med frontplate understøttet av ribber. Maksimal oppdemning over rørsenter er 2 mVS. I stengt stilling skrår lukebladet 25° i forhold til loddlinjen. Lukebredden er 3,5 m, og luken har ensidig “opptrekk”. For aktuell belastning skal maksimal vridningsspenning i lukebladet beregnes.
Midlere flatetrykk:
\[p = \gamma _f \cdot \rho \cdot g \cdot h/2 = 1,2 \cdot 1000 \cdot 9,81 \cdot 2 / 2 = \text{11 800 N/m}^2\qquad{(43)}\]
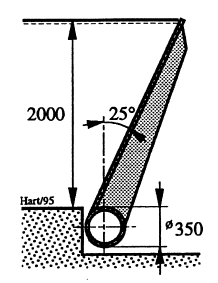
Vridningsmoment:
\[M_v = p \cdot B \cdot H \cdot (H/3) / \text{cos} 25 ^{\circ}\qquad{(44)}\]
\[= 11800\cdot 3,5 \cdot 2 \cdot (2/3) / \text{cos}25 ^{\circ} = \text{60 800 Nm}\qquad{(45)}\]
Her blir det røret i bunnen av lukebladet som må oppta vridningsbelastningen. Vridningsspenningen kan da beregnes vha. formelen i Kapittel 12.1 for sirkulært rør. Det regnes 1 mm rustfradrag på utvendig flate:
Vridningsspenning:
\[\tau _v = 16\cdot M_v \cdot d_y / (\pi \cdot (d_y ^4 - d_i ^4))\qquad{(46)}\]
\[= 16 \cdot \text{60 800 000}\cdot 348 / (\pi \cdot (348^4 - 310^4))=20\space \text{MPa}\qquad{(47)}\]
13 Flerakset spenningstilstand
13.1 Aktuelle formler
Når et punkt i en konstruksjon har flerakset spenningstilstand bestående av eksempelvis to hovedspenninger og en skjærspenning, beregnes jevnføringsspenning ved:
\[\sigma _j = (\sigma _1^2-\sigma_1\cdot\sigma_2+\sigma_2^2+3\cdot\tau^2)^{0,5}\qquad{(48)}\]
Et forhold man skal være spesielt oppmerksom på, er når 0 og 02 har motsatt tallverdi. Ofte blir det slike områder i en konstruksjon som får størst Gj. I noen tilfeller har man også mer komplisert spenningstilstand enn deri forannevnte. Aktuell formel for jevnføringsspenning blir da i det generelle tilfellet:
\[\sigma_j = (\sigma_x^2+\sigma_y^2+\sigma_z^2-\sigma_x\cdot\sigma_y-\sigma_y\cdot\sigma_z-\sigma_z\cdot\sigma_x+3\cdot\tau_{xy}^2+3\cdot\tau_{yz}^2+3\cdot\tau_{zx}^2)^{0,5}\qquad{(49)}\]
13.2 Eksempel: Jevnføringsspenning
I eksempelet i Kapittel 7.7 er tangensiell og aksiell spenning beregnet for et sylindrisk rør. Jevnføringsspenningen blir:
\[\sigma_j = (\sigma_t^2 - \sigma_t\cdot\sigma_a + \sigma_a^2)^{0,5} = (40^2-40\cdot20+20^2)^{0,5} = 34,6\space\text{MPa}\qquad{(50)}\]
14 Knekking av stav
14.1 Teoretisk grunnlag
Utsettes en stav for trykk-kraft F, kan det pga. små skjevheter oppstå utbøyning 5. I staven blir det da et bøyemoment M = F-ö som øker utbøyningen slik at denne i uheldige tilfeller vokse ut over enhver akseptabel grense, dvs. at staven knekker. Grensespenningen for dette, Og, kalles knekkspenning. Nøyaktig trykkspenningsberegning, i det det også tas hensyn til bøyespenning pga. utbøyningen, viser at lokal trykkspenning i det punkt hvor denne har høyest verdi, blir tilnærmet lik materialets flytegrense Op når knekkingen inntreffer [16].
Skal knekking behandles teoretisk, blir enkleste tilfelle en stav med konstant tverr-snitt, sentrisk belastet. Følgende størrelser har da betydning:
| Knekklengde lk : | lk for ulike stavinnspenninger fremgår bl.a. av NS 3472, tillegg A 5.4. For stav leddet i begge ender blir lk, lik stavlengden. |
| Rel. knekksp. σkre : | σkre = σk / σF |
| Treghetsradius i : | i = (I/A)0,5 |
| Slankhet λ : | λ = lk/i |
| Relativ slankhet λre : | λre = (λ/π)•(σF/E)0,5 = (lk/π)•(σF•A/(E•I))0,5 |
Knekkberegninger av stav utføres vanligvis iht. NS 3472. Her benyttes knekkingskurver fremstilt i diagram med relativ slankhet λre langs abscissen og relativ knekkspenning σkre langs ordinataksen. Videre gis det 3 ulike kurver A, B og C for ulike tverrsnittsformer. Tverrsnittsgraderingen tar hensyn til egenspenningene i tverrsnittene og reduserer det behov man tidligere hadde for ekstra høy sikkerhetsfaktor ved knekkberegninger.
Ønsker man å gjennomføre knekkberegningen aritmetisk, gir NS 3472 en tilnærmet matematisk beskrivelse av de nevnte kurver. Denne er:
\[\sigma_{kre} = +(1+\beta\cdot(\lambda_{re}-0,2)+\lambda_{re}^2)/(2\cdot\lambda_{re}^2) \newline -((1+\beta\cdot(\lambda_{re}-0,2) + \lambda_{re}^2-4\cdot\lambda_{re}^2)/(2\cdot\lambda_{re}^2))^{0,5}\qquad{(51)}\]
Konstanten β avhenger av tverrsnittsform. Knekkspenning henregnet til de tre kurvene A, B og C i NS 3472 fås ved innsetting av: βA=0,21 / βB=0,34 / βC=0,49
For knekking må man ellers merke seg at forholdet mellom materialspenning og den utbøyning som innledningsvis ble nevnt i dette kapittel, ikke er lineær. Av denne grunn kan man ved knekkberegninger ikke benytte superposisjon [16]. Eldre knekkformler som Eulers og Tetmajers bør man helst ikke bruke. Disse gir langt høyere tillatt spenning enn formelverket fra NS 3472 og krever sikkerhetsfaktor innen området 3 til 6. Eulerspenningen σE=π2•E/λ2 er imidlertid en størrelse som kan innsettes i uttrykket for relativ slankhet. En vil da se at λre=(σF/σE)^{0,5}.
14.2 Eksempel: Knekk-kontroll av opptrekkstang for luke
En opptrekkstang er laget av sirkulært rør, er leddet i hver ende, har lengde 12 m, ytterdiameter Ø200 mm og godstykkelse 10 mm. Det regnes 1 mm rustfradrag på utvendig flate. Stangmaterialet har σF=280 MPa og E=20,5•104 MPa. Last- og materialfaktor settes til henholdsvis γf=1,2 og γm=1,4. Største tillatte trykk-kraft skal bestemmes.
Knekk-kurve: B
Stangtverrsnitt: \[A = \pi\cdot(d_y^2-d_i^2)/4 = \pi \cdot (198^2-180^2)/4=5344 \space\text{mm}^2\qquad{(52)}\]
Tregh.moment: \[I = \pi\cdot(d_y^4-d_i^4)/64=\pi\cdot(198^4-180^4)/64=23,9\cdot10^6 \space\text{mm}^4\qquad{(53)}\]
Slankhet: \[\lambda = l_k/i = l_k\cdot(A/I)^{0,5} \newline = 12000 \cdot (5344/23,9\cdot10^6 )^{0,5} = 179\qquad{(54)}\]
Rel. slankhet: \[\lambda_{re} = (\lambda/\pi)\cdot(\sigma_F/E)^{0,5} \newline = (179/\pi)\cdot(280/20,5\cdot10^4)^{0,5}=2,11\qquad{(55)}\]
Avlest σkre: \[\sigma_{kre} = 0,185\qquad{(56)}\]
Knekksp.: \[\sigma_k = \sigma_{kre}\cdot\sigma_F=0,185\cdot280=51,8\space\text{MPa}\qquad{(57)}\]
Tillatt kraft: \[F_{maks} = \sigma_k\cdot A/(\gamma_f\cdot\gamma_m) = 51,8\cdot 5344/(1,2\cdot1,4) = \text{165 000 N}\qquad{(58)}\]
15 Knekking av plate
Teoretisk behandling av plateknekking er komplisert. For vannkraftutstyr refereres de vanligste problemstillingene nedenfor sammen med referanser for beregning av innknekkingstrykk når dette forutsettes jevnt fordelt over flaten.
Innknekking av rotasjonssymmetrisk endebund [3].
Innknekking av sylinderskall [3].
Innknekking av innstøpt sylindrisk rør [1].
Knekking av plan plate [12].
Et forhold som må vies oppmerksomhet ved slik beregning når man ikke benytter en anerkjent dimensjoneringsstandard, er hva som skal velges av sikkerhetsfaktor. For dette må en være klar over at sikkerhetsfaktoren skal inkludere beregningsusikkerheten. Det vises også til Kapittel 14.1 hvor det ble referert at nødvendig sikkerhetsfaktor ved knekkkontroll for stav med Eulers ligning er i området 3-6.
16 Utmatting
16.1 Konstruksjoner hvor utmatting bør undersøkes
Oppfatningen av når en konstruksjon kan være utmattingsutsatt, er ulik. Fra dimensjoneringsstandarder siteres.
DIN 19704 krever kontroll av en konstruksjons utmattingsfasthet når antall utsvingende eller vekslende belastninger overskrider antallet 2•106.
NS 3472 angir en spenningsvidde Δσ som er forskjellen mellom største og minste spenning. Oppfylles kravet Δσ < 1,5•σ0,2 og et tilsvarende krav for skjærspenningens spenningsvidde, tillates det at utmattingskontroll sløyfes hvis man for antall lastvariasjoner n har: n < 2•106•(36/Δσ)3
NS 470 opererer i utmattingssammenheng med 3 belastningstyper. Avhengig av n blir inndelingen:
Overveiende statisk belastning: n < 103 (n < 6•105)
Dynamisk belastning, liten utmattingseffekt: 103 < n < 6•105 (n > 6•105).
Dynamisk belastning, betydelig utmattingseffekt: n > 6•105 (Unntak)
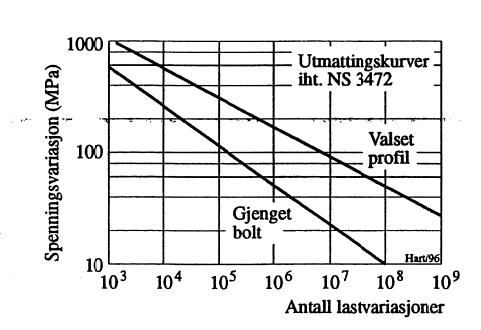
16.2 Utmattingsdiagrammer
Kontroll av utmatting i stålkonstruksjoner gjøres vha. Wöhler-diagram, eksempel vist i Figur 19.
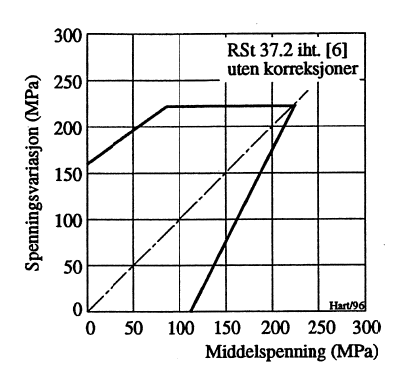
For utmattingsutsatte maskindeler som aksler, bolter, etc. har det også vært vanlig å benytte Smith-diagram, se Figur 20. Både Wöhler- og Smith-diagrammet forutsetter varierende belastning med konstant amplitude.
Med Wöhler-diagrammet kan man vanligvis bestemme antall lastvariasjoner før brudd som funksjon av spenningsvariasjonen når det forutsettes vekslende belastning. Det finnes imidlertid også spesielle Wöhler-diagrammer som er utarbeidet for sveiseforbindelser tas det hensyn til at det i sveisene er stående sveisespenninger, kjerver og mikrosprekker. Smith-diagrammet gir derimot tillatt spenningsvariasjon som funksjon av stasjonær spenning.
Verken Wöhler- eller Smith-diagrammet gir nøyaktige analyseresultater. Som regel vil det for de virkelige tilfellene være stor usikkerhet knyttet til den varierende belastnings karakteristika. Det at belastning sjelden varierer slik det ideelt sett forutsettes for bruk av diagrammene, er et annet forhold. Nyere bruddmekanikk har riktignok metoder som tar hensyn til sammensatte belastninger. Det ligger dog et problem i det at sprekkutviklingskonsekvensen ikke kun avhenger av de ulike belastningers størrelse, men også av deres innbyrdes rekkefølge.
16.3 Egensvingning ifm. varegrinder
I noen tilfeller vil utmattingsanalysen bestå i det å kontrollere at det ikke blir resonans mellom en konstruksjons egensvingefrekvens og eksiterende kraft. Dette er bl.a. aktuelt ifm. varegrinder. Bestemmelsen av frekvens gjeldende hydrauliske eksitasjon er for dette omtalt i manuskriptet “Strømningsteknikk i kraftverksvannvei”. Laveste svingefrekvens for en grindstav med tverrsnitt lstav’tstav, avstand mellom tverravstivningene lik L og lysåpning b blir: (π/2)•L-2•(E•I/(A•ρ))0,5. Ved svingningen vil imidlertid vannet i spaltene mellom grindstavene også delta i svingningen. Dette medfører at svingende masse øker og at egensvingefrekvensen blir lavere. Med gitte data kan stavfrekvensen tilnærmet angis som:
\[f_{stav} = \frac{\pi}{2\cdot L_{stav}^2}\cdot \sqrt{\frac{E\cdot I_{stav}}{l_{stav}\cdot(t_{stav}\cdot\rho_{stål}+b\cdot\rho_{vann})}}\qquad{(59)}\]
I formelen må det selvsagt benyttes tallverdier med enhetlige måleenheter.
16.4 Egensvingning ifm. platekasser
En platekasse består av kledning festet til innstøpte ribber. Med svingemode n kan egensvingefrekvensen for platen ved fri svingning i luft og med ribbene som forankringspunkter, beregnes med tilsvarende formel som angitt i Kapittel 16.3. Ulike svingemoder er anskueliggjort i Figur 21.
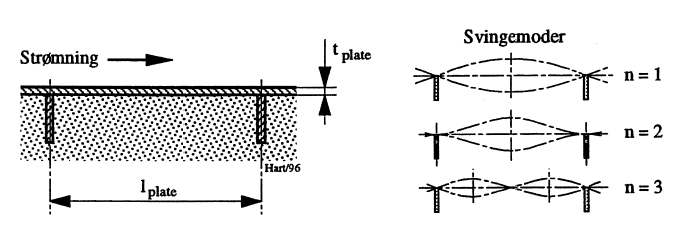
For et virkelig tilfelle vil platen være i kontakt med vann. Når platen svinger, vil også vannet delta i svingningen. Forholdet bidrar til økt svingende masse og redusert svingefrekvens. God innstøping av platekledningen kan på sin side bidra til endret svingemode.
Ligningen for svingefrekvensen blir:
\[f_{plate} = \frac{n\cdot\pi}{2}\cdot\frac{1}{l_{plate}^2}\cdot\sqrt{\frac{E\cdot I_{plate}}{\rho_{stål}\cdot A_{plate}}}\qquad{(60)}\]
Iplate og Aplate er treghetsmoment og platetverrsnitt regnet for enhetsbredde, eksempelvis:
\[I_{plate} = t_{plate}^3/12\space\space\text{(mm}^4\text{/mm)} \newline A_{plate} = t_{plate}\space\space\text{(mm}^4\text{/mm)}\qquad{(61)}\]
Benyttes enheten millimeter, må en huske at: ρstål = 7850 kg/m3 = 77•10-9 Ns2/mm4
16.5 Eksempel: Egensvingefrekvens for grindstav
En varegrind har tverrsnitt som vist i Figur 22.
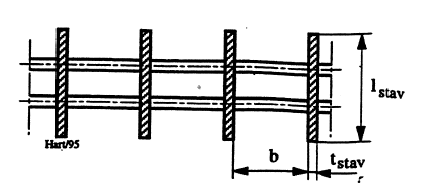
Stavlengde mellom avstivninger: \[L = 600 \space \text{mm} = 0,60 \space \text{m}\qquad{(62)}\]
Stavtverrsnittlengde: \[l_{stav} = 130 \space \text{mm} = 0,13 \space \text{m}\qquad{(63)}\]
Stavtverrsnitt-tykkelse: \[t_{stav} = 10 \space \text{mm} = 0,01 \space \text{m}\qquad{(64)}\]
Lysåpning: \[b= 60 \space \text{mm} = 0,06 \space \text{m}\qquad{(65)}\]
Elastisitetsmodul: \[E = 20,5\cdot 10^4 \space \text{N/mm}^2 = 20,5\cdot 10^{10} \space \text{N/m}^2\qquad{(66)}\]
Treghetsmoment: \[I= 0,13\cdot0,01^3/12= 108\cdot10^{-10} \space \text{m}^4\qquad{(67)}\]
Stavfrekvens: \[f=(\pi/2)\cdot L^{-2}\cdot[E\cdot I /(l_{stav}\cdot(t_{stav}\cdot\rho_{stål}+b\cdot\rho_{vann}))]^{0,5} \newline =(\pi / 2)\cdot 0,60^{-2}\cdot[20,5\cdot10^{10}\cdot108\cdot10^{-10} / (0,13\cdot(0,01\cdot7850 + 0,06\cdot1000))]^{0,5}\qquad{(68)}\]
Utregnet: \[f = 48,4\space \text{s}^{-1}\qquad{(69)}\]
17 Bruksgrensetilstand
17.1 Generelt om bruksgrensekontroll
Hva som menes med en konstruksjons bruksgrensetilstand, kan i utgangspunktet synes diffust. Uttrykket er å finne i Damforskriftene og i NS 3472, men blir ikke benyttet i DIN 19704, TBK og “Rules for Certification of Diving Systems”.
For stenge-/tappeorganer og rør sier Damforskriftene lite om hva denne type analyser skal omfatte. Bruksgrensetilstanden defineres imidlertid som: “Tilstand fastlagt i relasjon til kriterier som gjelder normal bruk eller varighet.” Mer presis blir formuleringen i NS 3472. Denne lyder: “I utmattingsgrensetilstanden skal konstruksjonen kontrolleres for;
deformasjoner som har betydning for den normale bruk av konstruksjonen,
vibrasjoner eller svingninger som gir ubehag eller påvirker bruk av konstruksjonen,
lokale skader som har betydning for konstruksjonens levetid.”
Ut fra dette kan det muligens hevdes at bruksgrensekontroll for stenge- og tappeorganer omfatter undersøkelse av;
at deformasjoner ikke blir så store at pakninger skades, eventuelt løftes fra anlegg,
at organet lar seg manøvrere,
at det innenfor det aktuelle driftsområdet ikke oppstår uakseptabel kavitasjon.
For rør er det vanskeligere å tenke seg hva bruksgrensekontroll måtte kunne omfatte. Ett forhold det imidlertid kan være grunn til å se på, er at det ved aktuell drift ikke blir så lavt trykk ved rørinnløp og luftinnslippingsventiler at det her suges luft. En kan også tenke seg at fastleggelse av driftsforhold og meteorologiske forhold hvor isdannelse inne i et frittliggende rør kan forekomme, er bruksgrensekontroll.
Ved bruk av last- og materialkoeffisienter, sier Damforskriftene med sine regler lite om hvilke verdier man ved bruksgrensekontrollen skal benytte. Mange har ved slike beregninger valgt å se bort fra de nevnte koeffisienter, men krever en viss margin ift. aktuelle grenseverdier. Ved dimensjonering av manøvreringsinnretningers kapasitet har eksempelvis flere kraftverkseiere/konsulenter fordret 20 % overkapasitet for uforutsett kraftbehov.
17.2
Skal deformasjoner bestemmes ved beregning, er det vanlig å benytte lineær elastisk teori. Dette innebærer at all deformasjon er proporsjonal med belastningen, hvilket også er essensen i Hooks lov. For enakset spenningstilstand med σ = materialspenning, E = elatisitetsmodul og ε = relativ forlengelse, kan Hooks lov skrives: σ = E•ε
For bjelker hvor M er bøyemomentet, I treghetsmomentet og x dimensjon i bjelkens lengderetning, kan deformasjonen y på differensiell form uttrykkes ved:
\[d^2y/dx^2 = -M/(E\cdot I)\qquad{(70)}\]
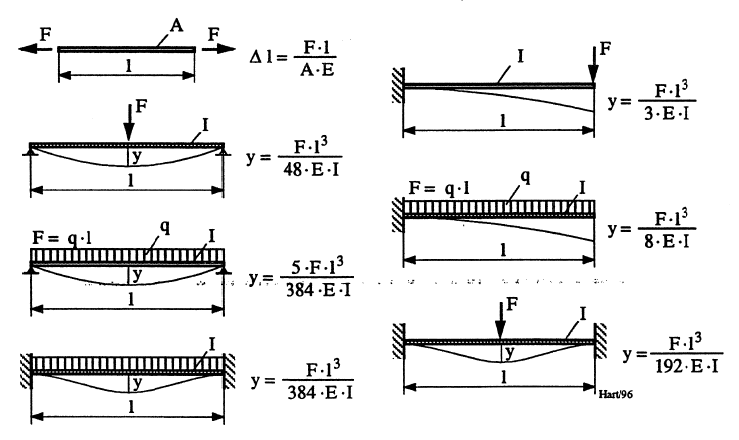
På basis av dette bestemmes deformasjonen for ulike belastningssituasjoner. Aktuelle tilfeller knyttet til konstruksjoner i kraftverksvannveien, gjengis i Figur 23. Eksemplene er hentet fra [5].
Ved andre belastningstilfeller kan man dobbelintegrere frem de deformasjoner man da har. Med regneark er det dessuten en praktisk mulighet å dele bjelkelengden l opp i mange små lengder Δx og så utføre integrasjonene ved summering over alle Δx. En har da:
Deformasjonsvinkel:
\[\phi_x=\Sigma(M/(E\cdot I))\cdot \Delta x + \text{konst}_1\qquad{(71)}\]
Deformasjon:
\[y_x = \Sigma \phi_x\cdot\Delta x +\text{konst}_2\qquad{(72)}\]
Konstantene bestemmes vha. aktuelle grensebetingelser.
Er det skjærspenninger τ som forårsaker deformasjoner, kan man i Hooks lov erstatte elastisitetsmodulen E med skjærmodulen G og relativ forlengelse ε med deformasjonsvinkel γv. Hooks lov blir da: τ=G•γv
Skjærmodulen kan finnes som funksjon av elastisitetsmodul og tverrkontraksjonstall ν ved uttrykket nedenfor.
\[G= E/(2\cdot(1+\nu))\qquad{(73)}\]
For stål med ν=0,3 blir: G= 20,5•104/(2•1,3)= 7,9•104 MPa.
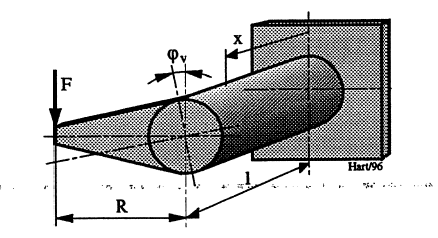
Ligningene foran kan benyttes for å bestemme deformasjonsvinkelen φv vist i belastingstilfellet i Figur 24. Generelt kan man for det aktuelle tilfellet når torsjonsmomentet Mv varierer som funksjon av x langs torsjonsstavens lengde l og Ip er det polare treghetsmomentet, uttrykke φv ved ligningen på neste side. Vinkelen angis her ved absolutt vinkelmål, mao. i radianer.
\[\phi_v = \frac{l}{G\cdot I_p}\cdot \int_{0}^{x}M_t\cdot dx = \frac{A_M}{G\cdot I_p}\qquad{(74)}\]
For tilfellet i Figur 24 er momentflaten: AM=F•R•l.. Lineær deformasjon ytterst på armen blir dessuten: y= φv•R
17.3 Eksempel: Kontroll av deformasjon for glideluke
En glideluke har lukeblad utført av massiv stålplate. Karakteristisk trykk er 50 mVS. Spennvidde og avstand mellom sidetetninger er 2000 mm. For stålplate med flytegrense 340 MPa er nødvendig platetykkelse pga. materialspenninger bestemt til 90 mm. For nevnte tykkelse må imidlertid også maksimal utbøyning beregnes.
Last pr. mm lukehøyde: \[F = \rho \cdot g \cdot h \cdot \Delta H\cdot B \newline = 1000\cdot 9,81 \cdot 50 \cdot 0,001 \cdot 2,00 = 981 \space\text{N}\qquad{(75)}\]
Treghetsmoment: \[I = \Delta H\cdot t^3 /12 = 0,001\cdot 90^3 /12 = \text{60 750 mm}^4 \qquad{(76)}\]
Utbøyning iht. Figur 23: \[y = 5 \cdot F\cdot l^3/(384\cdot E\cdot I)\newline =5\cdot 981\cdot 2000^3 / (384\cdot 20,5\cdot10^4\cdot 60750) = 8 \space\text{mm}\qquad{(77)}\]
Bemerkning: Utbøyningen vil sannsynligvis av hensyn til lukens topptetning ikke kunne aksepteres.
17.4 Eksempel: Kontroll av deformasjon for klappeluke
For en klappeluke skal vridningsdeformasjonen bestemmes. Snitt gjennom luken er vist i Figur 25 og luken har ensidig opptrekk. Utvendig krumningsradius for bukskallet er: Ry=1500 mm. Alle platetykkelser er: t=16 mm. Luken har bredde Bluke=10,00 m.
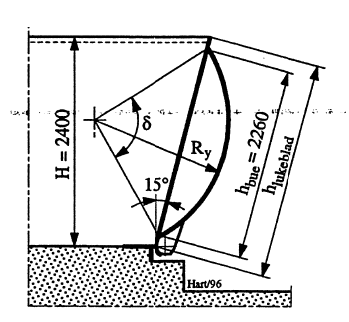
Lukebladets høyde: H_{lukeblad} = H/15^{} = 2400/15^{}= 2485 {#eq:vannkraft_vannvei_mekaniske-konstruksjoner_dimensjonering-utstyr-kraftverksvannveien_kap-16_eq16-4p1}
Buevinkel: \[\delta = 2\cdot \text{arcsin}(h_{bue}/(2\cdot R_y)) = 2\cdot \text{arcsin}(2260/(2\cdot 1500)) = 97,8^{\circ}\qquad{(78)}\]
Omkrets langs platers senterlinje (Rm = krumningsradius til senter bukplate): \[O_{omkr} = (h_{bue}-t)+2\cdot \pi\cdot R_m \newline = (2260-16)+2\cdot\pi\cdot(1500-8)=4791\space\text{mm}\qquad{(79)}\]
Tverrsnitt innskrevet platenes senterlinje: \[A_{innskr} = \pi\cdot R_m^2\cdot(\delta/360)+R_m^2\cdot\text{sin}(\delta/2)\cdot\text{cos}(\delta/2) \newline = R_m^2\cdot(\pi\cdot\delta/360+0,5\cdot\text{sin}\delta) \newline = (1500-8)^2 \cdot (\pi\cdot 97,8^{\circ} / 360^{\circ} + 0,5\cdot\text{sin}97,8^{\circ}) = \text{797 000 mm}^2\qquad{(80)}\]
Det polare treghetsmoment: \[I_p = 4\cdot A_{innskr}^2\cdot t/O_{omkr} = 4\cdot797000^2\cdot 16/4791=10,6\cdot 10^9 \space\text{mm}^4\qquad{(81)}\]
Vridningsmomentet Mv er har størst ved manøvreringssylinderens lukeside og null ved den andre siden. Maksimalt vridningsmoment: \[M_v = 0,5\cdot\rho\cdot g\cdot H\cdot h_{lukeblad}\cdot B_{luke}\cdot 0,333\cdot h_{lukeblad} \newline = 0,5 \cdot 1000\cdot 9,81\cdot 2,400\cdot 2,485\cdot 10,000\cdot 0,333\cdot 2,485 \newline = 242100\space\text{Nm}=0,2421\cdot 10^9\space\text{Nmm}\qquad{(82)}\]
Momentflate: \[A_{moment} = 0,5\cdot M_v\cdot B_{luke}\cdot 0,333\cdot h_{lukeblad} \newline = 0,5\cdot 0,2421\cdot 10^9\cdot 10000\cdot 0,333\cdot 2485 = 1210\cdot 10^9\space\text{Nmm}^2\qquad{(83)}\]
Vridningsvinkel: \[\phi_v = A_{moment}/(G\cdot I_p) \newline = 1210\cdot 10^9/(7,9\cdot 10^4\cdot 10,6\cdot 10^9) = 1,45\cdot 10^{-3} \space\text{rad} = 0,083^{\circ}\qquad{(84)}\]
Maksimal deformasjon i periferiretning: \[y = \phi_v\cdot h_{lukeblad} = 1,45\cdot 10^{-3}\cdot 2485 = 4\space\text{mm}\qquad{(85)}\]
Beregnes maksimal skjærspenning pga: vridningen”slik’dette’er Vist i Kapittel 12, får man forøvrig: τmaks=10 MPa
18 Litteratur
En liste over litteratur som kan være nyttig for den som ønsker å utdype sin kunnskap ifm. forhold presentert i dette dokument, er gitt nedenfor. Etter listen følger en kort omtale av de enkelte publikasjoner. Referansenummereringen overenstemmelser med referansene som er angitt som tidligere i dette dokument.
| Forfatter/redaktør. | Tittel | Utgiver | Referanse |
|---|---|---|---|
| Amstutz, Ernst. | Buckling of pressure-shaft | Water Power | [1] |
| Berdal Strømme. | Drift/vedlikeh. av kr.v.-rør. | EnFO. | [2] |
| Den norske trykkbeh.kom. | TBK | [3] | |
| DIN 19 704. | Stahlwasserbauten. | Beuth Verlag. | [4] |
| Dubbel. | Taschenbuch Maschinenbau. | Springer. | [5] |
| Hütte. | Des Ingenieurs Taschenbuch. | Ernst & Sohn. | [6] |
| Niemann, G. | Maschinenelemente. | Springer. | [7] |
| NS 3472 | Prosjektering av stålkonstruk. | NSF. | [8] |
| NVE | Forskrifter for dammer | Univeritetsforl. | [9] |
| Sundby, G. | Enkelte styrkeberegninger. | Tapir. | [10] |
| Sølsnes, . | Maskindeler, bind 1, 2 og 3. | Tapir. | [11] |
| Timoshenko, Stephen P. | Stability of Plates and Shells. | McGraw-Hill. | [12] |
| Timoshenko, Stephen P. | Theory of Plates and Shells. | McGraw-Hill. | [13] |
| Thomas, Kurt. | Stahl im Hochbau. | VDE. | [14] |
| Det norske Veritas | Sertification of Diving Systems | DNV | [15] |
| Waløen, Åge Ø. | Maskindeler, bind 1. | Tapir. | [16] |
| Young, Warren C. | Formulas for Stress & Strain | McGraw-Hill. | [17] |
| Nummer | Beskirvelse |
|---|---|
| [1] | Full tittel: “Buckling of pressure-shaft and tunnel linings”. Publisert i Water Power, november 1970. Artikkelen redegjør for og utleder det teoretiske grunnlaget for inn- knekkingskontroll av innstøpte sirkulære rør. |
| [2] | Rapporten er utarbeidet på oppdrag av EnFO og gjelder frittliggende rør. Det gis bl.a. omfattende orientering om hvilke krefter som virker på de nevnte rør. Det kreves ikke spesielle forkunnskaper av den som skal studere rapporten. |
| [3] | Dokumentet er en beregningsstandard og vil neppe ha interesse for andre enn dem som skal gjennomføre eller kontrollere styrkeberegninger. I eldre utgaver er det enkelte trykkfeil i presenterte formler. |
| [4] | Tysk stålkonstruksjonsnorm for bl.a. konstruksjoner i kraftverksvannveier. Det kan forøvrig påpekes at DIN 19705 angir krav til lukers manøvreringsinnretninger. Det er opplyst at DIN 19704 for tiden blir revidert. |
| [5] | Egentlig tittel: “Dubbels Taschenbuch fir den Maschinenbau”. Typisk tysk ingeniørhåndbok som tilsvarer Hütte I og IIA. Ny utgave som i det siste har utkommet som ett bind, er forholdsvis uhåndterlig. |
| [6] | Hütte I: “Teoretische Grundlagen”. Tysk ingeniørhåndbok som tilsvarer de generelle deler av [5]. |
| [7] | Lærebok i maskindeler utgitt på Springer Verlag 1963 og redigert av dr.ing. G. Niemann, professor ved den tekniske høgskole i München. |
| [8] | Norsk standard for dimensjonering av stålkonstruksjoner. Sammen med Damforskriftene er denne standard nærmest enerådende som mal ved dimensjonering av norske kraftverksluker. |
| [9] | Offentlige bestemmelser fastsatt ved kongelig resolusjon av 14. nov. 1980 gjeldende utførelse av dammer med tilhørende installasjoner. |
| [10] | Heftet er utgitt på Tapirs forlag i 1943 og må i dag anses som et faghistorisk kuriosa for de spesielt vannkraftinteresserte. Fra forordet kan det siteres: “Det var erfaring fra konstruksjonsundervisningen ved Høgskolens Maskinavdeling som ga støtet til at det fra omkr. 1920 ble medtatt et særskilt avsnitt om enkelte styrkeberegninger under forelesningene over Vannkraftmaskiner. Således syntes det å være behov for bedre kjennskap til de prinsipper som ligger til grunn for beregningene …..” |
| [11] | Lærebøker i maskindimensjonering benyttet ved NTH på 50- og 60-tallet |
| [12] | Medforfatter for boken er James M. Gere. Boken behandler knekkingsproblematikk for bjelker og skall. |
| [13] | Medforfatter for boken er S. Woinowsky-Krieger. Boken behandler bøyebelastninger og deformasjoner i plater, rektangulære såvel som sirkulære, plane og krumme. Knekkingsproblematikk behandles ikke. Boken er teoretisk og krevende. Som ingeniørhåndbok blir den mindre egnet. Dog kan den være verdifull for den som må utlede egne formler. |
| [14] | Håndbok for planlegging, beregning og utførelse av stålkonstruksjoner utgitt av VDE (Verein deutscher Eisenhüttenleute), Düsseldorf. Boken er på nærmer 1000 sider og inneholder beregningsformler og et utall profildata. |
| [15] | Full tittel: Rules for Certification of Diving Systems. Utgitt 1988. Beregningsstandarden har bl.a. vært benyttet for innknekkingskontroll ifm. endebunder utsatt for utvendig overtrykk. Den er nå trukket tilbake og erstattet av internasjonale standarder. |
| [16] | Lærebok i maskindeler benyttet ved NTH og enkelte ingeniørhøgskoler. Boken er presenterer en rekke tekniske materialer og utfyller på mange måter [2]. |
| [17] | Formelsamling på nærmere 800 sider. Innen området styrkeberegning synes denne boken å være den mest komplette av sitt slag som er i markedet. Boken er imidlertid ingen lærebok. |
