HÅNBOK - TEORI: STRØMNINGSTEKNIKK I KRAFTVERKSVANNVEIEN
En kortfattet innføring med eksempler.
1 Innledning
Forfatter: Ragnar Hartmann, Statkraft Engineering as 18.09.97
Dette manuskript er betalt av Energiforsyningens Fellesorganisasjon (EnFO) og kan fritt benyttes ved alle EnFOs nåværende og fremtidige kurs. Bruk til andre formål, omarbeidelser eller videre bearbeiding krever forfatters godkjennelse. Statkraft Engineerings eventuelle bruk av manuskriptet skal ikke skje slik at dette kommer i konkurranse med EnFOs virksomhet. Privatpersoner har anledning til å ta enkeltkopier når formålet er egen opplæring. Ved kopiering ut over dette for andre enn EnFo, Statkraft Engineering eller forfatter, må tillatelse på forhånd være innhentet fra EnFO. Manuskriptet tillates ikke benyttet som referanse ved beregninger vedr. sikkerhet eller når resultatet kan medføre betydelig økonomisk konsekvens.
2 Hensikt og målsetting
Dette kompendium er laget i tilknytning til et kurs om luker, ventiler, rør og varegrinder. Kompendiet behandler strømningstekniske forhold knyttet til nevnte vannveisutstyr, men er ingen lærebok i strømningsteknikk. Kompendiets primære oppgave skal være å bidra til økt forståelse for strømningstekniske spørsmål. At det samtidig gir et sammendrag av sentrale problemstillinger og refererer de mest aktuelle formler, er derimot i utgangspunktet ikke gjort for å kvalifisere leseren til gjennomføring strømningstekniske analyser med stor betydning for sikkerhet og økonomi. Slike beregninger bør fortsatt overlates spesialister.
Kompendiets målgruppe er personell i kraftforsyning og ved vannverk. At den enkelte på forhånd har strømningsteknisk innsikt, kan være fordelaktig, men ingen betingelse. Fordi det hos kursdeltagerne forventes ulike forhåndskunnskaper samtidig som aktuell forelesningstid er begrenset, har man illustrert teorien med eksempler. Disse forutsettes gjennomgått ved selvstudium.
For den som siden måtte ønske å fordype seg i faget, er det i kapittel 18 gitt litteraturliste. Denne fungerer også som referanseliste for dette dokument.
Mest sentralt står de generelle strømningsligninger og anvendelsen av disse. Dette omfatter ligninger for både væske- og gass-strømning. Væskestrømningslovene er viktige ved kapasitetsbestemmelser og fastleggelse av krefter. Luftstrømningsproblematikk blir av betydning ved enkelte sikkerhetsmessige forhold.
I stor utstrekning er det slik at strømningstekniske forhold er med på å forme funksjonskravene som stilles til utstyret i vannveien. Trykk og impulskrefter har relevans ved fastleggelse av dimensjoneringskriterier, mens ikke-stasjonære strømningsforhold reiser problemstillinger relatert til sikkerhet og pålitelighet. Der hydrauliske pulsasjoner gir utmattingseffekt, og dynamiske forhold kombinert med resonans gir mulighet for betydelige ekstrabelastninger, er det ikke gitt at noen ekstra mm stål i platetykkelsene bedrer funksjonen. Kunnskap om nevnte forhold er av betydning for den som forestår drift og vedlikehold.
Kompendiets anvendte målesystem er iht. SI, men de fleste formler har ubenevnte konstanter og er slik sett dimensjonsuavhengige. Unntak fra dette gjelder tilstandsligningen for gass og Mannings formel for beregning av hydraulisk friksjonstap i tunneler.
3 Symboler
Anvendte symboler er sammen med aktuelle måleenheter angitt i listen nedenfor:
| Symbol | Beskrivelse |
|---|---|
| a | hastighet for trykkbølge i lukket vannvei, lydhastighet (m/s). |
| afull | full lukeåpning målt fra luketerskel (m). |
| aluke | lukeåpning målt fra luketerskel (m). |
| astr | overflate på utstrømning fra luke målt fra luketerskel (m). |
| b | lukeåpnings bredde eller lysåpning mellom staver i varegrind (m). |
| c | strømningshastighet (m/s). |
| ckr | lydhastighet i gass (m/s). |
| cp | spesifikk varme for gass ved isobar tilstandsendring (J/kg K). For luft: cp = 1000 J/kg K. |
| d | rørdiameter (m) |
| dh | hydraulisk diameter (m). dh = 4•A / fuktet periferi. |
| f | frekvens (s-1). |
| g | gravitasjonskonstant (m/s2). Verdi: g= 981 m/s2. |
| h | dybde i væske, også benyttet ved angivelse av trykk (m). |
| Δh | hydraulisk friksjonstap (m). |
| k | absolutt ruhet for strømningsflate (analog sandkornstørrelse) (m). |
| l | rørlengde, tunnellengde, kanallengde (m). |
| m | masse (kg). |
| p | trykk i gass eller væske (Pa, bar). I Pa= 1 N/m?, 1 bar = 10? N/m?. |
| pd | damptrykk i væske (Pa, bar). |
| pk | trykk i tverrsnitt med gass-strømning hvor hastigheten er lik lydhastighet. |
| po | omgivelsestrykk (Pa, bar). Vanligvis po = ca. 1,0 bar. |
| r | radius (m). |
| t | tid (s). |
| t | temperatur (°C). |
| tstav | avløpskantbredde for varegrindstav (m). |
| x | karakteristisk lengde for dimensjonsløse tall (m). |
| y | forhold mellom karakteristiske lengder i modell og prototyp (ubenevnt). |
| z | stedshøyde ift. referanseplan (m). |
| å | åpningsgrad for luke/ventil (ubenevt). å = a/afull |
| A | areal (m2). |
| E | spesifikk hydraulisk energi benyttet i IEC-spesifikasjoner for hydrauliske maskiner (J/kg). |
| F | kraft (N). |
| Fr | Froudes tall (ubenevnt). For kanalstrømning: Fr=c/(g•x)0,3 |
| H | høydeforskjell (m). |
| Htun | høyde i tunneltverrsnitt (m). |
| I | kanalhelning (ubenevnt). I = høydeforskjell bunn / kanallengde. |
| M | Mannings tall (m/s). |
| Q | volumstrøm (m/s). |
| R | gasskonstant (J/kg K). For luft: R = 287 J/kg K. |
| Re | Reynolds tall (ubenevnt). For rørstrømning: Re=c•dh/ν |
| Rh | hydraulisk radius (m). Rh = A / fuktet periferi = 0,25 - dh. |
| St | Strouhals tall som benyttes ved beregning av frekvens ved virvelavløsningsfrekvens (ubenevnt). For varegrindstav: St= f-tsav/c= 0,12. St må ikke forveksles med Stantons tall. |
| T | absolutt temperatur (K). 0 K = -273 °C, 273K = O°C. |
| α | utstrømningskoeffisient (ubenevnt). |
| β | helningsvinkel lukeblad og grind (°). |
| ε | relativ ruhet for strømningsflate (ubenevnt). €= k/ dy. |
| ζ | singulærtapskoeffisient (ubenevnt). |
| κ | isentropeksponent for gass (ubenevnt). For luft: κ = 1,4. |
| λ | friksjonskoeffisient for rør (ubenevnt). |
| ν | kinematisk viskositet (m2/s). For vann i kraftverk: ν = ca. 1,2•106 m2/s |
| ρ | densitet for væske eller gass (kg/m). ρvann = 1000 kg/m. |
| σ | kavitasjonsparameter (ubenevnt). |
| φ | hastighetskoeffisient (ubenevnt). |
4 Hydraulisk trykk i væsker og gasser
Gravitasjonskrefter medfører at det på en flate A i væskedybde h virker et hydraulisk trykk p og en kraft F. Trykket defineres som kraft pr. flateenhet og har retning normalt flaten. Er gravitasjonskonstanten g og væskens densitet p, blir trykk og kraft henholdsvis:
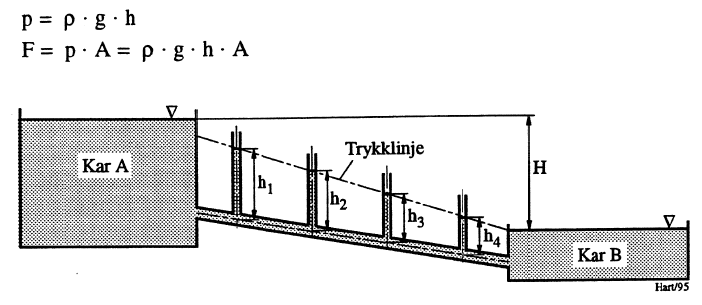
En enkel sammenheng gjelder mellom væskedybde h og hydraulisk trykk p når væsken er inkompressibel, dvs. har konstant densitet. For praktiske vurderinger knyttet til kraftverksluker, ventiler, rør, varegrinder, etc, vil dette i de aller fleste tilfeller kunne forutsettes. En konsekvens blir da at væsketrykk kan angis som høyden av vertikal væskesøyle fra det aktuelle sted i væsken og opp til fri overflate. Dette illustreres ved Figur 1 hvor det gjennom et rør strømmer væske fra kar A til kar B.
At trykklinjen synker fra kar A til kar B, skyldes strømningen og det faktum at det i røret er strømningsmotstand, friksjon. Dette blir nærmere berørt i Kapittel 23. Det kan også nevnes at trykklinjen ville gått horisontalt ut fra overflatenivået i kar A dersom røråpningen til kar B var blitt plugget.
Gass er et medium hvor man som regel må ta hensyn til kompressibilitet. For gass gir tilstandsligningen en sammenheng mellom trykk, densitet og temperatur.
\[p = \rho \cdot R \cdot T\qquad{(1)}\]
En forskjell mellom angitt gass- og væsketrykk er at gasstrykket fastsettes ift. absolutt vakuum, mens væsketrykket vanligvis regnes relativt til omgivelsestrykket.
Ofte forekommer betegnelsene statisk og dynamisk trykk. Statisk trykk blir det trykk som måles i en væske når denne er i ro. Dynamisk trykk er en mer upresis betegnelse. I noen tilfeller kan dette forstås som “hastighetshøyde”, se Kapittel 6.
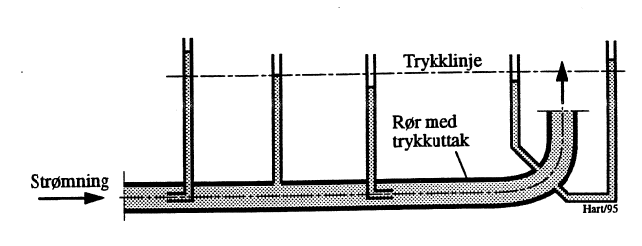
At trykkmålinger avhenger av hvordan det enkelte trykkuttak er utført, illustreres ved Figur 2. Fordi strømningshastigheten er konstant gjennom røret samtidig som det ses bort fra friksjonstap, blir trykklinjen horisontal. Forøvrig bør figuren kunne tale for seg selv.
En noe spesiell størrelse, “spesifikk hydraulisk energi” E, forekommer i IEC-spesifikasjoner for hydrauliske maskiner. Fordi det her kreves at E skal benyttes i stedet for fallhøyde/ løftehøyde H, blir E av enkelte oppfattet som et trykk. E er imidlertid, som navnet tilsier, en energistørrelse med benevning J/kg. Ifm. kraftverksluker, ventiler, rør og grinder har E til nå vært lite aktuell. Nærmere omtale av størrelsen vil man eksempelvis finne i IEC- spesifikasjon 41, “Field Acceptance Tests [12].
4.1 Eksempel
I røret nedstrøms en ventil synker vanntrykket til -1,50 mVS. Luft slippes da inn i røret. Er omgivelsestrykket 1,000 bar og densiteten for vann 1000 kg/m3, blir absolutt trykk inne i røret:
\[p_{rør} = p_o+\rho \cdot g \cdot h = 1,000 + (1000\cdot 9,81\cdot(-1,50)\cdot10^{-5}) = 0,853 \space\text{bar}\qquad{(2)}\]
5 Trykk- og impulskrefter
Trykk-krefter er omtalt i Kapittel 4. Dette er krefter som har sammenheng med det hydrauliske trykket i en væske eller gass.
Er mediet i bevegelse, oppstår det også krefter på grunn av hastighetsendringer, dvs. når strømningshastigheten endrer størrelse eller retning. Disse krefter kalles impulskrefter og er generelt gitt ved ligningen nedenfor hvor c1 og c2 må oppfattes som vektorer.
\[F = \rho \cdot Q\cdot (c_1-c_2)\qquad{(3)}\]
5.1 Eksempel
Fylleventil er innebygget i en høytrykks stengeluke og vist i Figur 3. Maksimal trykkdifferanse over ventilen vil være 80 mVS virkende fra venstre i figuren. Hydraulisk åpne-/stengekraft skal bestemmes for ventilposisjoner hvor impulskreftene kan neglisjeres.
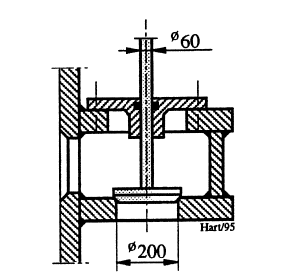
Åpnekraft: \[F_{hydr,åpne} = \rho \cdot g\cdot \Delta h\cdot \pi\cdot (d_{vent}^2-d_{stang}^2)/4 \newline F_{hydr,åpne} = 1000\cdot 9,81\cdot 80\cdot \pi\cdot (0,200^2 -0,060^2)/4= \space\text{22 400 N}\qquad{(4)}\]
Stengekraft: \[F_{hydr,åpne} = \rho \cdot g\cdot \Delta h\cdot \pi\cdot d_{stang}^2/4 \newline F_{hydr,åpne} = 1000\cdot 9,81\cdot 80\cdot \pi\cdot 0,060^2/4= \space\text{2 220 N}\qquad{(5)}\]
5.2 Eksempel
Et rørbend er plassert i en rørgate. Bendet har innløpsdiameter Ø1200 mm og utløpsdiameter Ø1000 mm. Bendet gir retningsendring for strømningen i rørgaten fra 30° ift. horisontalplanet ved innløp til 45° ved utløp. Pga. ekspansjonsbokser oppstrøms og nedstrøms bendet må alle hydrauliske krefter som oppstår ifm. dette overføres til bendets fundament. Som forutsetninger for en beregning settes volumstrømmen lik 8,50 m/s og innvendig trykk lik 103 mVS. Aktuelle tverrsnitt og hastigheter kan angis til:
- Innløpstverrsnitt: 1,131 m2
- Utløpstvertsnitt: 0,785 m2
- Strømn.hast. innløp: 7,515 m/s
- Strømn.hast. utløp: 10,828 m/s
Figur 4. viser bend med påførte krefter slik disse er beregnet i det etterfølgende. Ved beregningen gis krefter som virker i strømningsretningen fortegn pluss. Krefter som virker mot strømningsretningen er minus.
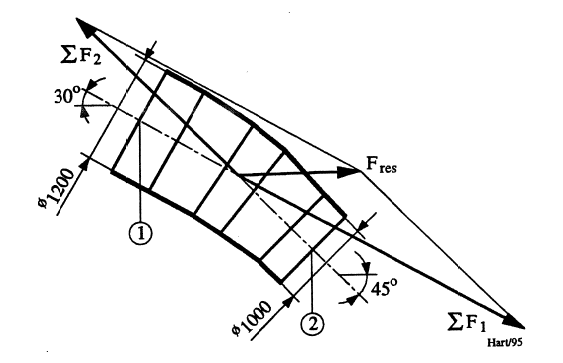
Trykk-kraft, innløp: \[F_{1t} = \rho\cdot g\cdot h_1\cdot A_1 = 1000\cdot 9,81\cdot 103\cdot 1,131 = \space\text{1 148 000 N}\qquad{(6)}\]
Impuls, innløp: \[F_{1i} = \rho\cdot Q\cdot c_1 = 1000\cdot 8,5\cdot 7,515 = \text{64 000 N}\qquad{(7)}\]
Sum, innløp: \[\Sigma F_1 = \text{1 212 000 N}\qquad{(8)}\]
Trykk-kraft, utløp: \[F_{2t} = \rho\cdot g\cdot h_2\cdot A_2 = 1000\cdot 9,81\cdot 103\cdot 0,785 = \space\text{- 794 000 N}\qquad{(9)}\]
Impuls, utløp: \[F_{2i} = \rho\cdot Q\cdot c_2 = 1000\cdot 8,5\cdot 10,828 = \text{- 92 000 N}\qquad{(10)}\]
Sum, utløp: \[\Sigma F_2 = \text{- 886 000 N}\qquad{(11)}\]
Kraftresultanten Fres beregnes ved dekomponering i vertikale og horisontale komponenter. I det nye koordinatsystem har krefter med fortegn +, retning horisontalt mot høyre eller vertikalt oppover.
\[F_{1h} = 1212\cdot \text{cos}30^{\circ}=\space+\space1050 \text{kN} \hspace{35pt} F_{1v}= 1212\cdot \text{sin}30^{\circ}=\space-\space606 \text{kN} \newline F_{2h} = -886\cdot \text{cos}45^{\circ}=\space -\space 626 \text{kN} \hspace{35pt} F_{2v}= -886\cdot \text{sin}45^{\circ}=\space+\space626 \text{kN} \newline \Sigma F_h = \space +\space 424 \space\text{kN} \hspace{35pt} \Sigma F_v = \space + \space 20 \space\text{kN}\qquad{(12)}\]
Kraftresultant: \[F_{res} = [(\Sigma F_h)^2+(\Sigma F_v)^2]^{0,5} = [424^2 + 20^2]^{0,5} = 454\space\text{kN}\qquad{(13)}\]
6 TrykkTapsfri væskestrømning
Sammenhengen mellom stedshøyde, trykkhøyde og hastighetshøyde i en væskestrøm gis av Bernoullis ligning. Med z lik stedshøyden, h lik trykkhøyden, c lik strømningshastigheten og g lik gravitasjonskonstanten kan ligningen for tapsfri strømning skrives som vist nedenfor. Enkelte omtaler forøvrig hastighetshøyden c2/2g som det dynamiske trykk.
Bermoullis ligning:
\[z+h+c^2/2g = \text{konstant}\qquad{(14)}\]
En annen viktig strømningsligning er kontinuitetsligningen. Når væskens densitet kan an- ses konstant, uavhengig av trykket, blir kontinuitetsligningen:
Kontinuitetsligningen: \[ c\cdot A = \text{konstant}\qquad{(15)}\]
Vanligvis benyttes Bernoullis ligning mellom to tverrsnitt, A1 og A2. Kjenner man tverrsnittene, kan man eksempelvis da vha. kontinuitetsligningen uttrykke c1 med c2.
6.1 Eksempel
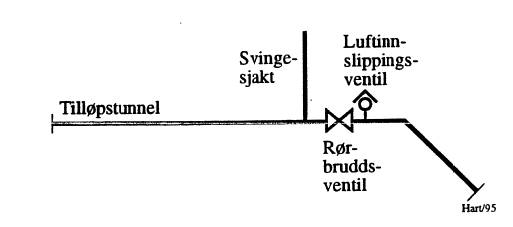
Del av et kraftverkssystem med svingesjakt, rørbruddsventil og luftinnslippingsventil er vist i Figur 5. Tilløpstunnelen har 18 m2 tverrsnitt, og gjennomstrømningstverrsnittet i rørbruddsventilen er 2,5 m2. Luftinnslippingsventilen står montert direkte på kraftverks- røret. Nivået er her 67,3 moh. Av luftinnslippingsventilens dokumentasjon fremgår det at denne skal åpne ved 0,065 bar trykkdifferanse (undertrykk i røret).
For turbinvannføring 26 m^2/s skal man fastlegge laveste vannstand i svingesjakten før luftinnslippingsventilen åpner.
To strømningstverrsnitt defineres. Tverrsnitt 1 er strømningstverrsnittet i tilløpstunnelen - der svingesjakten kommer ned i denne. Tverrsnitt 2 er tverrsnittet umiddelbart nedstrøms rørbruddsventilen hvor luftinnslippingsventilen står montert. Som strømningsareal kan man her sette rørbruddsventilens areal.
Hastigheter: \[c_1 = Q/A_1 = 26/18 = 1,44 \space\text{m/s} \newline c_2 = Q/A_2 = 226/2,5 = 10,4\space\text{m/s}\qquad{(16)}\]
Åpnetrykk: \[h_2 = -\Delta p /(\rho\cdot g) = -0,065\cdot10^5/(1000\cdot 9,81) = -0,663 \space\text{m}\qquad{(17)}\]
Bernoulli fra 1 til 2: \[z_1 +h_1+c_1^2/2g = z_2 +h_2+c_2^2/2g \newline 67,3 + h_1 + 1,44^2 / 19,62 = 67,3 - 0,663 + 10,4^2 / 19,62 \newline 67,3 + h_1 + 0,106 = 67,3 - 0,663 + 5,513\qquad{(18)}\]
Utregnet: \[h_1 = 4,74\space\text{mVs}\qquad{(19)}\]
Laveste nivå i sjakt: \[z_1 + h_1 = 67,3 + 4,74 = 72,04 \space\text{moh.}\qquad{(20)}\]
6.2 Eksempel
Figur 6 viser en forenklet spjeldventil med kvadratisk gjennomstrømningstverrsnitt. Spjeldet står i 30° delåpning som vist. Det skal for denne situasjonen beregnes resulterende hydraulisk moment på spjeldet når det samtidig forutsettes at vannhastigheten ut fra ventilen er 20 m/s, at strømningen etter spjeldet har en kontraksjon på 0,8, at strømningen er tapsfri og at spjeldet er sentrisk opplagret.
Beregningen som i det etterfølgende blir presentert er meget forenklet. Dog kan det være aktuelt å beregne moment på virkelig spjeldventil etter samme prinsipp når man ikke har måleresultater fra modellforsøk eller prototyp.
Langs spjeldets underside vil strømningen ha variabelt trykk som påvirker kreftene de hydrauliske kreftene. Slik strømningsbildet er antydet, påvirkes derimot ikke spjeldets overside. Langs denne forutsettes det konstant trykk som forenklet settes lik 0 m. For bestemmelse av trykket langs undersiden legges det videre inn 6 snitt loddrett strømlinjene. Tilnærmet lar man snittene representeres ved rette linjer med 15° helning i forhold til det vertikale. Snittene nummereres 1 til 6 i strømretningen.
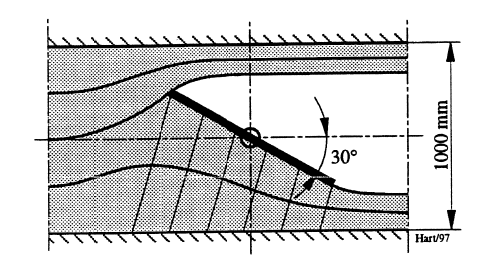
Lengden av snitt 6 blir: L6=(500 - 500•sin 30°)/cos 15°= 259 mm. Hastigheten i snitt 6 finnes vha. oppgitt kontraksjon: c6= 0,8•20=16 m/s. Det er forutsatt 0 m trykk etter spjeldet. Bernoulli gir da: h6=0+202/19,62-162/19,62=7,34 m. Tilsvarende beregninger for alle snitt føres i tabell.
| Snitt nr: | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Snittlengde (m): Hastighet (m/s): Trykk (m): | 0,776 5,3 18,96 | 0,673 6,2 18,43 | 0,569 7,3 17,67 | 0,466 8,9 16,35 | 0,362 11,4 13,76 | 0,259 16,0 7,34 |
Deretter beregnes midlere trykk mellom snittene og tilhørende momentarm fra opplagringsaksen. Til slutt beregnes så de hydrauliske momentene mot spjeldflatene mellom snittene. Størrelsen av disse flatene er 0,2•1,0 = 0,2 m2.
| Flate mellom snitt: | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 |
|---|---|---|---|---|---|
| Midlere trykk (m): Kraft (N): Moment (Nm): | 18,70 36700 14680 | 18,05 35400 7080 | 17,01 33400 0 | 15,06 29500 -5900 | 10,55 20700 -8280 |
Moment pga. veggtrykk langs spjeld: 14680 + 7080 + 0 - 5900 - 8280 = 7580 Nm
I tillegg vil det også oppstå et moment som følge av avbøying av vannstrømmen ved spjeldets forkant. Forutsettes det at denne kraften virket mellom snitt 1 og 2 hvor hastigheten blir: c1-2 = (202 - 19,62 - 18,70)0,5 =5,8 m/s, og at midlere retningsforandring er 20°, kan kraften beregnes vha. impulsligningen.
\[\text{Impuls} = \rho \cdot Q\cdot c\cdot \text{sin}\alpha= 1000\cdot (1,0\cdot 0,259\cdot 16)\cdot5,8\cdot \text{sin}20^{\circ}=\text{8220 N}\qquad{(21)}\]
Moment pga. impulskraft: 8220•0,4 = 3290 Nm
Resulterende moment på spjeld: 7580 + 3290 = 10 900 Nm
7 Tapsfri gass-strømning
Ved gass-strømning har man vanligvis fire forskjellig ligninger som angir forholdet mellom tilstandsstørrelsene.
Energiligningen: \[c_p\cdot T + c^2/2=\text{konstant}\qquad{(22)}\]
Isentropligningen: \[T_1/T_2 = (p_1/p_1)^{(\kappa-1)/\kappa}\space\space\space\text{eller}\space\space\space p_1/p_2 = (\rho_1/\rho_2)^\kappa\qquad{(23)}\]
Kontinuitetslign.: \[\rho\cdot c \cdot A= \text{konstant}\qquad{(24)}\]
Tilstandsligningen: \[p=\rho \cdot R\cdot T\qquad{(25)}\]
Produktet cp•T i energiligningen er gassens termiske energi, entalpi, med benevning J/kg. Som man ser av energiligningen blir det derfor gassens entalpi som ved hastighetsakselerasjon går over til kinetisk energi. Dette skjer som isentropisk tilstandsendring, dvs. ved konstant entropi. Prosessen blir i mindre grad reversibel. Skal således hastighetsenergi omdannes til trykkenergi, er dette vanligvis forbundet med betydelige tap. Riktignok øker også da gassens entalpi, men samtidig skjer det en økning av gassens entropi.
Det siste er tilfelle når luft strømmer med stor hastighet og følgelig lav temperatur ned i en lukesjakt. Etter hvert som hastigheten dempes ved friksjon, vil temperaturen igjen stige til det den var før akselerasjonen.
Som et spesielt forhold ved gass-strømning kan nevnes at strømningshastigheten vanligvis ikke overskrider grenseverdien ckr som er lydhastigheten i gassen. For luft som strømmer fra et tverrsnitt I til et tverrsnitt 2, vil hvis hastigheten c1 er neglisjerbar, hastigheten c2 bli lik lydhastigheten ckr dersom forholdet mellom p2 og p1 er lik det kritiske trykkforhold. Dette kan for luft settes lik: pkr/p1 = 0,529 [3].
7.1 Eksempel
Fra lukehuset for en tappeluke er det i gulvet en 0,5 m2 åpning til lukesjakten. Under forutsetning av at det under dekket kan oppstå et undertrykk tilsvarende -2 mVS, skal maksimal lufthastighet med tilsvarende minimums temperatur bestemmes. Trykk og temperatur for tilstrømmet luft til lukehuset forutsettes å være p1= 1,00 bar og t1= -10 °C. Lufthastigheten i lukehuset settes tilnærmet lik 0 m/s.
Trykk i åpning:
\[p_2 = p_1 - \rho\cdot g\cdot h = 1,00-1000\cdot 9,81\cdot (-2)/10^5 = 0,804\space\text{bar}\qquad{(26)}\]
Trykkforholdet p2/p1 er større enn det kritiske trykkforhold pkr/p1- Dette medfører at c2 blir mindre enn ckr.
Isentropisk endring: \[T_1/T_2 = (p_1/p_1)^{(\kappa-1)/\kappa} \newline T_2 = T_1/(p_1/p_1)^{(\kappa-1)/\kappa} \newline T_2 = (273-10)/(1,00/0,804)^{(1,4-1)/1,4}=247\space\text{K} \newline t_2 = 247-273 = -26^{\circ}\text{C}\qquad{(27)}\]
Energiligningen: \[c_p\cdot T_1 + c_1^2/2 = c_p\cdot T_2 + c_2^2/2 \newline 1000\cdot 263 + 0 = 1000\cdot 247 + c_2^2 /2 \newline c_2 = (2\cdot 263000-2\cdot247000)^{0,5} = 179 \space\text{m/s}\qquad{(28)}\]
7.2 Eksempel
Luftinnslippingsventilen i eksempel Kapittel 6.1 har fritt gjennomstrømningstverrsnitt 0,05 m2. En mulig stenging av rørbruddsventilen ved den spesifiserte turbinvannføring gjør det nødvendig å bestemme laveste innvendige trykk i røret. For forenkling av beregningen forutsettes det at rørbruddsventilen og luftinnslippingsventilen stenger/åpner momentant og samtidig.
Ved den aktuelle problemstilling er høy temperatur på inngående luft ugunstig. Denne settes derfor lik 20 °C. Videre forutsettes det at lufthastigheten gjennom luftinnslippingsventilen blir lik lydhastighet.
Trykk i ventil: \[p_2 = p_1\cdot p_{kr}/p_1 = 1,00\cdot 0,529=0,529\qquad{(29)}\]
Isentropisk endring og lufttemp. i ventil: \[T_1/T_2 = (p_1/p_2)^{(\kappa-1)/\kappa} \newline T_2=T_1/(p_1/p_2)^{(\kappa-1)/\kappa} \newline T_2 = (273+20)/(0,529)^{(1,4-1)/1,4}=244\space\text{K}\qquad{(30)}\]
Energiligningen: \[c_p\cdot T_1 + c_1^2/2=c_p\cdot T_2+c_2^2/2 \newline 1000\cdot 293 + 0 = 1000\cdot 244 + c_2^2/2 \newline c_2 = (2\cdot 293000-2\cdot 244000)^{0,5} = 313\space\text{m/s}\qquad{(31)}\]
Volumstrøm ventil: \[Q_{vent} = c_2\cdot A_{vent} = 313\cdot 0,05 = 15,7\space\text{m}^3\text{/s}\qquad{(32)}\]
Tilstandsligningen: \[\rho_2=p_2/(R\cdot T_2) = 0,529\cdot 10^5 / (278\cdot 244) = 0,755 \space\text{kg/m}^3\qquad{(33)}\]
Fordi Qvent er mindre enn Qturb, må trykket inne i røret bli lavere enn p2 slik at luften utvider seg og ved dette får et volum som tilsvarer det tappede vannvolum. For videre beregning forutsettes det derfor at Qvent ekspanderer til Qturb Og at massestrøm ρ•Q gjennom ventil og inne i rør er like.
Massestrøm: \[\rho_2\cdot Q_2 = \rho_{rør}\cdot Q_{turb} \newline \rho_{rør} = \rho_2\cdot Q_2/Q_{turb} = 0,755\cdot 15,7/26 = 0,456 \space\text{kg/m}^3\qquad{(34)}\]
Isentropisk eksp.: \[p_2/p_{rør} = (\rho_2/\rho_{rør})^\kappa \newline p_{rør} = p_2\cdot (\rho_{rør}/\rho_2)^\kappa = 0,529\cdot (0,456/0,755)^{1,4}=0,261 \space\text{bar}\qquad{(35)}\]
Trykk i rør: \[h_{rør} = (p_{rør}-p_1)/(\rho\cdot g) \newline h_{rør} = (0,261 - 1,00)\cdot 10^5 / (1000\cdot 9,81) = -7,53 \space\text{mVs}\qquad{(36)}\]
Lufttemp i rør: \[T_{rør} = T_1 /(p_1/p_{rør})^{(\kappa-1)/\kappa} \newline T_2 = (273+20)/(1,00/0,261)^{(1,4-1)/1,4}=200 \space\text{K} = -73\space^{\circ}\text{C}\qquad{(37)}\]
8 Væskestrømning med tap
Ved strømningsberegninger kan man ta hensyn til friksjonstap ved at det i Bernoullis ligning innføres friksjonsledd Δh. Disse blir i kraftverkssystemer proporsjonale med kvadratet av volumstrømmen og følgelig også proporsjonale med kvadratet av strømningshastigheten. Bernoullis ligning mellom to tverrsnitt 1 og 2 kan da skrives:
\[z_1 + h_1 + c_1^2/2g = z_2+h_2+c_2^2/2g+\zeta\cdot c_2^2/2g\qquad{(38)}\]
Friksjonsleddet er: (ζ•c222/2g). For enkelte tilfeller kan det imidlertid være praktisk å omskrive dette til: Δh = konstant•Q2. Nærmere angivelser av koeffisienten ζ fremgår av de etterfølgende kapitler.
8.1 Eksempel
To vannfylte kar har en 0,017 m2 rørforbindelse. Nivåforskjellen mellom karenes overflater er 4,00 m. Røråpningene ligger under de respektive overflater. Friksjonstapet i røret er ved rørstrømningshastighet 3,0 m/s målt til 2,00 mVS. Systemet tilsvarer det system som ble vist i Figur 1. Ut fra de gitte data kan man bestemme volumstrømmen fra det ene kar til det annet.
En velger å regne med Bernoullis ligning fra punkt I (overflaten i det kar vannet strømmer fra) til punkt 2 (utstrømningsåpningen i det kar vannet strømmer til). Som referansenivå velges laveste overflate. Utstrømningsåpningens nivå er ikke kjent og settes lik den ukjente størrelse - z2. Ettersom åpningen ligger i dybde z2, blir følgelig h2=+z2.
Friksjonstap: \[\Delta h_{1-2} = \zeta\cdot c_2^2/2g\qquad{(39)}\]
Innsatt: \[2,00=\zeta \cdot3,0^2/19,62\qquad{(40)}\]
Bernoulli: \[z_1 + h_1 + c_1^2/2g = z_2 + h_2+c_2^2/2g+\zeta\cdot c_2^2/2g \newline 4,00 + 0+0=-z_2 + z_2 + (1 + 4,36)\cdot c_2^2/19,62 \newline c_2 = (4,00\cdot 19,62/5,36)^{0,5} = 3,83\space\text{m/s}\qquad{(41)}\]
Volumstrøm: \[Q = c_2\cdot A_2=3,83\cdot 0,017= 0,0651\space\text{m}^3\text{/s}\hspace{0,75cm}\text{Dvs.:65,1 l/s}\qquad{(42)}\]
8.2 Eksempel
Tre magasiner er forbundet som vist i Figur 7. Figuren angir tapsleddene for forbindelsens enkelte grener. Ut fra dette kan volumstrømmen i de ulike grener beregnes.
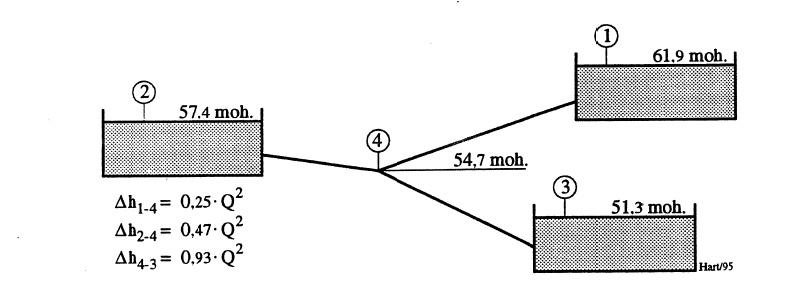
For beregningen forutsettes det at hastighetshøyden i den enkelte gren er liten ift. tapsleddet og at hastighetshøyden følgelig kan neglisjeres uten at dette får praktisk betydning for beregningsresultatet. Likeledes ser man bort fra tapene i knutepunktet 4. Med nevnte forenklinger fås 3 ligninger med 4 ukjente størrelser.
\[Q_{1-4}^2=(61,9-54,7-h_4)/0,25=28,8-h_4/0,25 \newline Q_{2-4}^2=(57,4-54,7-h_4)/0,47=5,74-h_4/0,47 \newline Q_{4-3}^2=(54,7-51,3+h_4)/0,93=3,66+h_4/0,93\qquad{(43)}\]
En fjerde ligning er kontinuitetsligningen. Regnes Q2-4 som en størrelse med negativt fortegn når strømningen skjer fra 4 til 2, blir kontinuitetsligningen:
\[Q_{1-4}+Q_{2-4}-Q_{4-3}=0\qquad{(44)}\]
En praktisk fremgangsmåte for løsing ligningssettet blir her å anvende grafisk metode. Da antas ulike verdier for h4, hvorpå grenvannføringene utregnes og kontrolleres vha. kon- tinuitetsligningen, se nedenfor. Resultatet inntegnes i diagram, Figur 8.
| h4 (mVs): | 300 | 3,50 | 4,00 |
| Q1-4 (m3/s): | 4,10 | 3,85 | 3,58 |
| Q2-4 (m3/s): | -0,80 | -1,31 | -1,66 |
| h4 (mVs): | 3,00 | 3,50 | 4,00 |
| Q4-3 (m3/s): | 2,62 | 2,72 | 2,82 |
| Q1-4+Q2-4-Q4-3 (m3/s): | +0,68 | -0,18 | -0,90 |
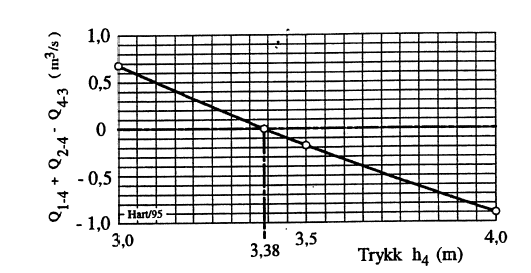
Utregnet med h4=3,38 m: Q1-4=3,91 m3/s Q2-4=-1,21m3/s Q4-3=2,70 m3/s
9 Strømningstap i tunneler og rør
Ved strømning i tunneler og rør og benyttes ulike formler for bestemmelse av friksjonstapet. Størrelsene M og λ blir å oppfatte som friksjonskoeffisienter.
Rør - Dårcy-Weisbachs formel:
\[\Delta h = \lambda\cdot (l_{rør}/d_h)\cdot c^2/2g\qquad{(45)}\]
Tunneler - Mannings formel:
\[\Delta h = l_{tunnel}\cdot c^2/(M^2\cdot R_h^{4/3})\qquad{(46)}\]
I tilknytning til Darcy-Weisbachs og Mannings formel bør man merke seg enkelte særegenheter.
Mens friksjonen i Darcy-Weisbachs formel øker med økende λ, øker tunnelfriksjonen i Mannings formel med minskende M.
Sammenhengen mellom hydraulisk diameter og hydraulisk radius er: dh=4•Rh. For rør med sirkulært tverrsnitt blir: dh=d og Rh=R/2.
Konstanten i Darcy-Weisbachs formel er dimensjonsuavhengig. Manning-tallene som refereres i det etterfølgende, har benevningen: m1/3/s.
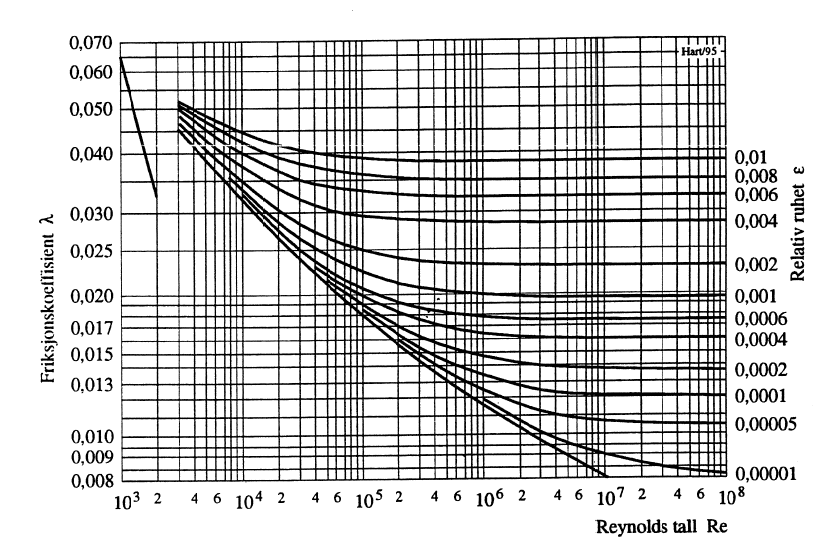
Ved rørberegning med Darcy-Weisbachs formel kan λ bestemmes vha. Moodys diagram, se Figur 9. Dette forutsetter at Reynolds-tallet Re og rørets relative ruhet ε er kjent. Størrelsene er gitt ved:
\[Re = c\cdot d_h/\nu\hspace{1cm}\text{og}\hspace{1cm}\varepsilon=k/d_h\qquad{(47)}\]
Her er ν vannets kinematiske viskositet og k rørveggens absolutte ruhet. Ulike ruhetsverdier angis i det etterfølgende. Tabellen for de ulike rørtyper er hentet fra referanse [5].
| Nye glatte stålrør: | k=0,0025 mm |
| Stålrør med glatt malingsbelegg: | k=0,0025 mm |
| Sementbelagte stålrør: | k=0,05 - 0,1 mm |
| Stålrør med noe rust: | k=0,25 mm |
| Rør med ujevnt tykt asfaltbelegg: | k=0,5 mm |
| Sterkt korroderte stålrør: | k=1,0 mm |
| Stålrør med rusttuberkler: | k=1,2mm |
| Støpejernsrør, med/uten belegg: | k=0,15 mm |
| Glatte betongrør med glatte skjøter: | k=0,1 mm |
| Betongrør med ugunstig innv. flate: | k=1,0-2,0 mm |
Ved høyere Reynolds-tall blir det entydig sammenheng mellom friksjonskoeffisienten Å og den relative rørruheten ε, se Figur 9. Prandtle og Nikuradse har satt denne sammenhengen lik:
\[\lambda = (2\cdot \text{lg}(d_h/k)+1,138)^{-2}\qquad{(48)}\]
Mannings formel som vanligvis benyttes ved fastleggelse av hydraulisk friksjonstap i tunnel, har for råsprengte tunneler som regel et Mannings-tall i området 30-35 m1/3/s. Verdi ved overslagsberegninger kan være 33 m1/3/s. Det tilstrebes å benytte virkelig strømningshastighet, basert på virkelig tverrsnitt.
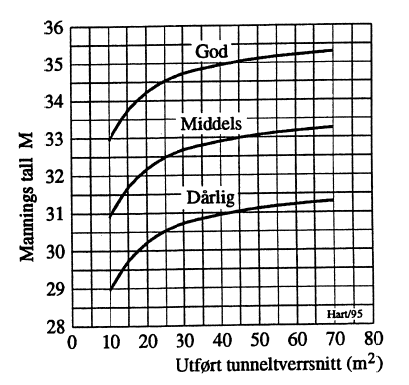
I beregninger blir det ofte hensiktsmessig å erstatte hastighet c med volumstrøm Q. Anvendes i Mannings formel tilnærmelsen Rh=A0,5/4, gjøres ved dette for vanlige tunneltverrsnitt med halvsirkel og rektangel langt mindre feil enn virkningen av usikkerheten i Manningstallet. Med metrisk system blir: Δh=(6,32•ltunnel/(M2•A2,567))•Q2. En studie av falltap i tunneler er dokumentert i [2]. Tabell med Manning-tall som funksjon av tverrsnitt og utførelse for råsprengte tunneler er hentet fra denne kilde og gjengitt i Figur 10. Det kan utledes at sammenhengen mellom Darcy-Weisbachs koeffisient og Manning-tall blir:
\[\lambda = 8\cdot g/(M^2\cdot R_h^{1/3}) = 8\cdot g\cdot 4^{1/3} / (M^2\cdot d_h^{1/3}) = 12,7\cdot g/(M^2\cdot d_h^{1/3})\qquad{(49)}\]
Singulærtap representert ved avgreninger, sjakter, nisjer, etc., inngår ikke når den angitte M-verdi benyttes. Det må også påpekes at M egentlig avhenger av tunneloverflatens beskaffenhet, tunneltverrsnittets størrelse og den aktuelle strømningsretning ift. tunnelens driveretning. For sistnevnte forhold kan det opplyses at tapet blir minst når vannet strømmer mot driveretningen. NHL har ved modellforsøk [2] kommet til at forholdet mellom Manning-tallene for en råsprengt tunnels to retninger med indekser referert til driveretningen, blir: Mmot/Mmed=1,22
For fullprofilborede tunneler er Manning-tall målt i området 63 - 68 m1/3/s. Som gjennomsnittsverdi foreslås: M = 65 m1/3/s.
Med utgangspunkt i Manning-tallene i Figur 10, omregningsformelen til Darcy-Weisbachs koeffisient λ og dernest Prandtle-Nikuradses sammenheng mellom λ og absolutt rørruhet k, blir sistnevnte størrelse som gitt nedenfor. Absolutt ruhet for fullprofilboret tunnel refereres til Manning-tall 64 - 67 m1/3/s samt diameterområdet 2,0 - 3,0 m.
| Råspengt tunnel med “god” overflate: | k = 0,17 - 0,19m |
| Råspengt tunnel med “middels” overflate: | k = 0,23 - 0,24 m |
| Råspengt tunnel med “dårlig” overflate: | k = 0,30 - 0,32m |
| Fullprofilboret tunnel: | k = 0,003 - 0,005 m |
9.1 Eksempel
Et tunnelprofil har bredde 5 meter og høyde 6 meter. Tunneltaket er utformet som 180° sylinderflate spennende fra vegg til vegg. Med vannføring 50 m3/s skal strømningstapet beregnes for 1600 meter tunnellengde. Det forutsettes Manning-tall M = 33.
Tunneltverrsnitt: \[A = 5\cdot 3,5+0,5\cdot \pi\cdot 5^2/4= 27,32\space\text{m}^2\qquad{(50)}\]
Fuktet omkrets: \[O = 5+3,5+3,5+0,5\cdot \pi\cdot 5=19,85\space\text{m}\qquad{(51)}\]
Hydraulisk radius: \[R_h = A/O=27,32/19,85=1,38\space\text{m}\qquad{(52)}\]
Strømningshast.: \[c = Q/A = 50/27,32=1,83\space\text{m/s}\qquad{(53)}\]
Mannings formel: \[\Delta h = l_{tunnel}\cdot c^2 /(M^2\cdot R_h^{4/3}) \newline \Delta h = 1600\cdot 1,83^2 / (33^2\cdot 1,38^{4/3})=3,20\space\text{mVs}\qquad{(54)}\]
10 Kanalstrømning
Strømningsligninger for kanal kan avledes av uttrykkene i Kapittel 9. Tar man utgangspunkt i Darcy-Weisbachs formel og forutsetter konstante strømningsforhold i kanalens lengderetning, kan kanalens helning I settes lik friksjonsmotstanden pr. meter kanallengde, Δh/lkanal. Sluttproduktet av utledningen som gjøres nedenfor, blir vanligvis omtalt som Chezys formel. Et tilsvarende uttrykk kan selvsagt også avledes fra Mannings formel.
\[\Delta h = \lambda \cdot (l_{kanal}/d_h)\cdot c^2/2g \newline c = (\Delta h \cdot d_h\cdot 2g/(\lambda\cdot l_{kanal}))^{0,5} = (8,9/\lambda^{0,5})\cdot (R_h\cdot I)^{0,5}\qquad{(55)}\]
10.1 Eksempel
En kanal hvor det strømmer vann, har tverrsnitt som vist i Figur 11. For kanalen som er utstøpt, kan absolutt ruhet settes til I mm. I kanalens lengderetning synker bunnen 4 mm pr. meter. Skal volumstrømmen i kanalen bestemmes, kan aktuell fremgangsmåte bli som angitt nedenfor. Her har man valgt å benytte Darcy-Weisbachs formel.
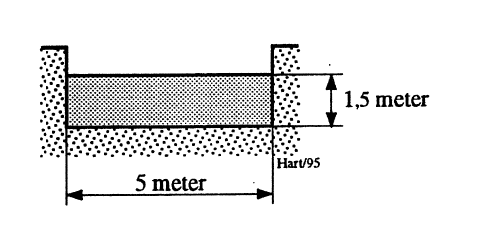
Fuktet overflate: \[O= 1,5 + 5,0 + 1,5 = 8,0 \space\text{m}\qquad{(56)}\]
Areal: \[A= 1,5-5,0 = 7,5 \space\text{m}^2\qquad{(57)}\]
Hydraulisk diameter: \[d_h=4\cdot A/O = 4\cdot 7,5/8,0= 3,75 \space\text{m}\qquad{(58)}\]
Relativ ruhet: \[\varepsilon = k/d_h = 0,001/3,75=2,7\cdot 10^{-4} \newline\qquad{(59)}\]
Hastighet (λ=0,02): \[c = (\Delta h\cdot d_h\cdot 2g/(\lambda\cdot l_{kanal}))^{0,5} \newline c = (0,004\cdot 3,75\cdot 19,62/(0,02\cdot 1))^{0,5}=3,84 \space\text{m/s}\qquad{(60)}\]
Reynolds tall: \[Re = c\cdot d/\nu = 3,84\cdot 3,75/1,2\cdot 10^{-6}=\text{12 000 000}\qquad{(61)}\]
Med de beregnede verdier for ε og Re finner man fra Moodys diagram, Figur 9, ny verdi for λ. Denne blir 0,0144.
Hastighet (λ=0,0144): \[c = (\Delta h\cdot d_h\cdot 2g/(\lambda\cdot l_{kanal}))^{0,5} \newline c = (0,004\cdot 3,75\cdot 19,62 /(0,0144\cdot 1))^{0,5} = 4,52\space\text{m/s}\qquad{(62)}\]
Ny beregning av Re og ny avlesning av λ er etter dette ikke nødvendig fordi man ved første avlesning lå på den horisontale delen av ε-kurven. Økt Reynolds-tall endrer derfor ikke λ.
11 Strømning ved terskel/overløp
Det teoretiske grunnlag for strømning over terskel er beslektet med teorien for kapasitetsbestemmelse ifm. klappeluker, sektorluker og gummiluker. I noen tilfeller vil terskler eller overløp også innvirke på vannstander som blir bestemmende for luker kapasitet. Et tredje tilfelle hvor denne teori kommer til anvendelse er ved frispeilstrømning gjennom et lukeløp hvor luken står i fullt åpen stilling. En overløpsstrømning er prinsipielt vist i Figur 12.
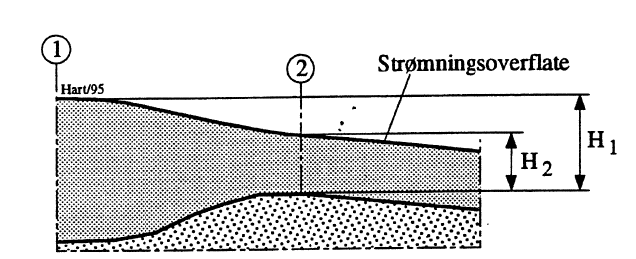
Forutsettes det at kanalbunnen etter snitt 2 har konstant helning og at strømningen her ikke retarderes, kan forholdene analyseres vha. Bernoullis ligning. Ettersom det hydrauliske trykket i snitt 2 øker lineært fra 0 mVS ved overflaten til H2 ved bunnen, blir det akselererende trykk for alle strømlinjer fra snitt 1 til snitt 2: H1-H2. Dette gir med tapsfri strømning:
\[c_{2teor} = (2\cdot g\cdot (H_1-H_2)+c_1^2)^{0,5}\qquad{(63)}\]
Vannføringen kan etter dette finnes vha. uttrykket nedenfor hvor: c2virkelig=φ•c2teor.
\[Q = \phi \cdot (2\cdot g\cdot (H_1-H_2)+c_1^2)^{0,5}\cdot b\cdot H_2\qquad{(64)}\]
Uttrykket er ikke entydig i det Q varierer avhengig av H2 ift. H1. I virkeligheten innstiller imidlertid H2 seg slik at Q får størst mulige verdi. Matematisk kan det påvises ved enkel maksimumsberegning for c1=0 m/s og tapsfri strømning når maksimalvannføring inntreffer:
Maksimal Q ved: H2/H1=0,667
11.1 Eksempel
Nedstrøms en tappeluke er det bygget en svakt krummet terskel. Terskeltopp ligger på nivå 66,8 moh. Terskelbredden er 90 m. Terskelen innvirker på tappelukens bakvannsnivå. Det er derfor behov for å utarbeide kapasitetskurve for terskelen gjeldende vannføringsområdet 0-14 m3/s.
Av hensyn til forenkling ser en bort fra strømningshastigheten oppstrøms terskelen. Antas det hastighetskoeffisient φ=0,9 , blir aktuell formel:
\[Q = 0,9\cdot (2\cdot 9,81\cdot 0,333\cdot H_1)^{0,5}\cdot 90\cdot 0,667\cdot H_1\qquad{(65)}\]
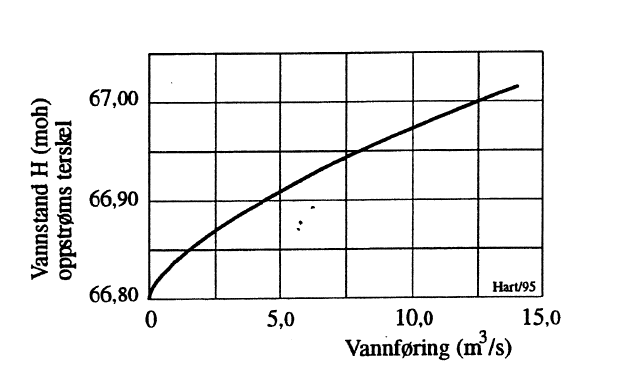
Formelen kan med fordel programmeres for beregning i regneark hvorved kapasitetskurven også kan tegnes. Resultatet blir som vist i Figur 13.
12 Lukekoeffisienter
En lukes evne til nøyaktig vannføringsregulering kan være viktig. Særlig gjelder dette der det er konsesjonsgitte krav om tapping forbi et kraftverk.
Kommer utstrømningen fra lukens underkant, kan strømningsbildet bli som vist i Figur 14. Forutsettes det tap slik at en del av vannets energi går over til varme mellom snitt 1 og snitt 2, kan hastigheten vha. Bernoullis ligning uttrykkes:
Utløpshastighet:
\[c_2 = \phi\cdot [2\cdot g\cdot (h_1-h_2+z_1-z_1)+c_1^2]^{0,5}\qquad{(66)}\]
Vannføring: \[Q = \alpha\cdot A\cdot [2\cdot g\cdot (h_1-h_2+z_1-z_2)+c_1^2]^{0,5}\qquad{(67)}\]
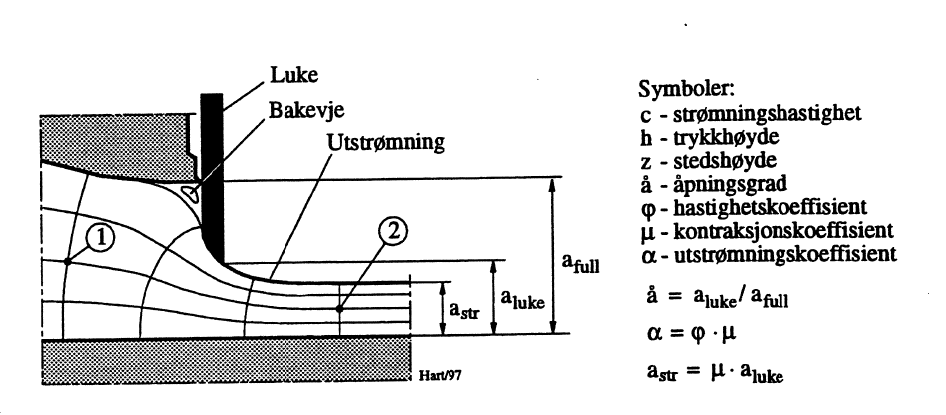
Forutsettes det at strømningen fra snitt 1 til snitt 2 er tapsfri, at H er høydeforskjellen mellom vannoverflaten oppstrøms luken og lukens bunnterskel, at de hydrauliske tap i oppstrøms system frem til snitt 1 er Δh=konst•Q2, at lukens underkant kan heves til høyde afull og at dens faktiske posisjon over luketerskelen er aluke, kan ligningen skrives:
\[Q = \mu\cdot b\cdot a_{luke}\cdot [2\cdot g\cdot (H-\mu\cdot a_{luke}-\text{konst}\cdot Q^2)]^{0,5}\newline\text{eller}\newline Q = \mu\cdot å\cdot b\cdot a_{full}\cdot [2\cdot g\cdot (H-\mu\cdot å\cdot a_{full}-\text{konst}\cdot Q^2)]^{0,5}\qquad{(68)}\]
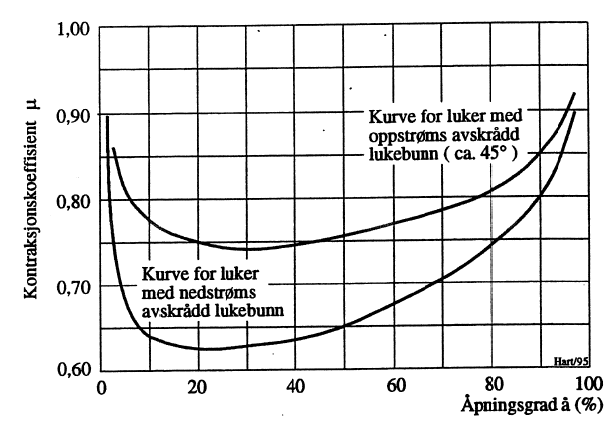
Aktuelle verdier for kontraksjonskoeffisienten μ ifm. plane lukeblad fremgår av [8] og gjengis i Figur 15. Kurvene er imidlertid knyttet til helt spesielle utforminger av lukebladene. I tillegg påvirkes μ av H når denne nærmer seg åfull. Forholdene er søkt illustrert i Figur 16.
Er lukebladet krumt slik tilfellet blir for en segmentluke, har kurvene i Figur 15 ingen gyldighet. For dette kan det refereres til [10] hvorfra kapasitetsdataene i Figur 17 er hentet.
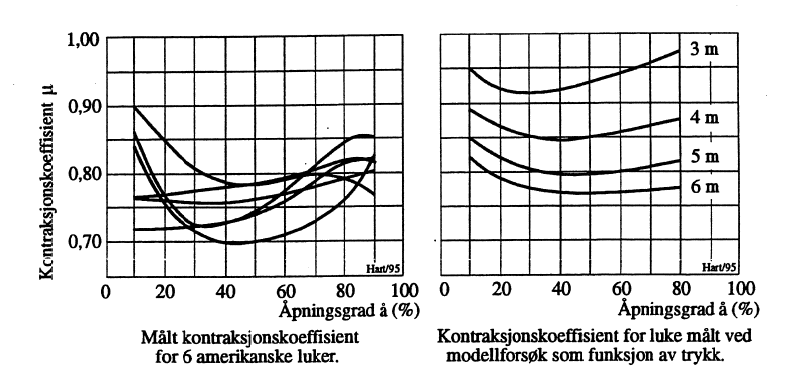
Knekkpunktene som er angitt for aluke/H=0,637 tilsvarer H2/H1; som ved forenklinger er beregnet til 0,667 i Kapittel 11. Fysisk betyr aluke/H=0,637 at vannoverflaten for strømningen gjennom lukeløpet her synker under lukebunnen.
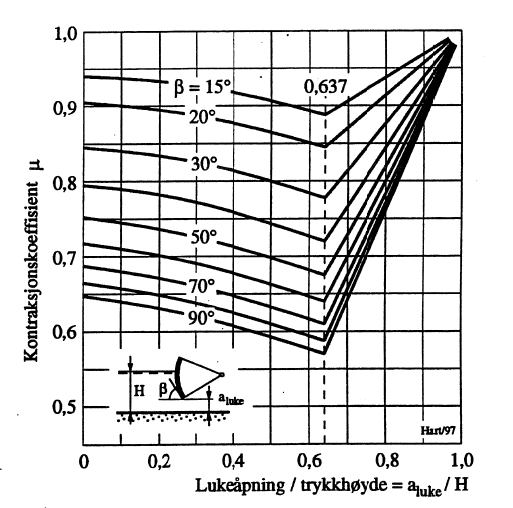
Det understrekes at kontraksjonskoeffisientene i Figur 17 kun gjelder lukeløp med plan bunn. Krummer bunnen slik forholdet ofte er ved flomluker, får koeffisientene andre verdier. For illustrasjon av dataenes presisjon, kan det refereres til modelldata publisert av U.S. Army Corps of Engineers gjeldende en luke ved Garrison. Dette er en segmentluke med plan bunn, dvs. samme forutsetning som i Figur 17. Ved β=60° har denne luken forholdstall aluke/H=0,37 og kontraksjon μ=0,705. Avlesning i Figur 17 gir μ = 0,68.
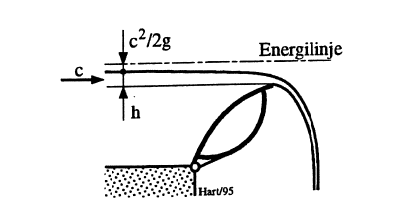
For luker som vannet renner over, kan det likeledes refereres til [10]. Figur 18 viser en klappeluke. Forutsettes det ideell stømning over lukekanten, hvilket bl.a. medfører at strålen skal være fullstendig luftet, angir [10]:
\[Q = 0,667\cdot \mu\cdot b\cdot (2g)^{0,5}\cdot ((h+c^2/2g)^{1,5}-(c^2/2g)^{1,5})\qquad{(69)}\]
Ved ulike utførelser av luketoppen vil μ variere i området 0,5 til 0,8. Er toppen skarpkantet, blir ifølge [10]: μ=0,64.
For overslagsberegninger kan man sette c=0 m/s. Med skarpkantet luketopp fås:
\[Q_{overslag}=1,9\cdot b\cdot h^{1,5}\qquad{(70)}\]
12.1 Eksempel
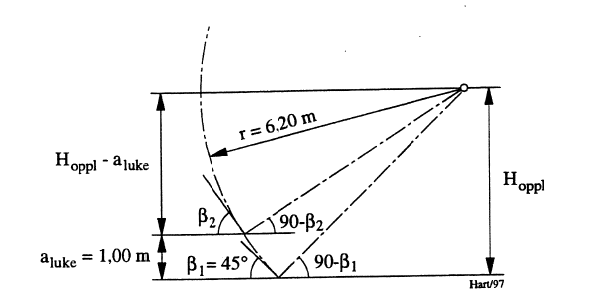
For en segmentluke med bredde b=8,00 m er bunnvinkelen i lukket posisjon β1 = 45°. Radius fra opplagring til frontskjold er r=6,20 m. Lukeløpet har horisontal bunn med vannstand H=3,50 m over denne. Ved lukeåpning aluke/H=1,00 m skal vannføringen gjennom lukeløpet bestemmes. Eventuell oppstuvning nedstrøms luken neglisjeres. Geometridata fremgår av Figur 19.
\[H_{oppl} = r\cdot \text{sin}(90-\beta_1)=6,20\cdot\text{sin}45^{\circ}=4,38\space\text{m} \newline H_{oppl}-a_{luke} = r\cdot \text{sin}(90-\beta_2) \newline \text{sin}(90-\beta_2) = (4,38-1,00)/6,20 = 0,545\hspace{1cm}\text{Dvs.:}\space\space\beta_2=57^{\circ} \newline\newline a_{luke}/H/H = 1,00/3,50 = 0,29\qquad{(71)}\]
Avlest fra diagrammmet i Figur 18: μ=0,71
I det det ses bort fra hydrauliske tap oppstrøms luken, blir vannføringen:
\[Q = \mu\cdot b\cdot a_{luke}\cdot (2\cdot g\cdot H)^{0,5} \newline Q = 0,71\cdot 8,00\cdot 1,00\cdot (2\cdot 9,81\cdot 3,50)^{0,5} = 47\space\text{m}^3\text{/s}\qquad{(72)}\]
12.2 Eksempel
En tappeluke, utført som glideluke, er montert i tunnel med Atunnel=20 m2, Rh=2,6 m Og ltunnel=3 km. Lukens dimensjoner er: b x afull=1,70 x 3,00 m2. Luken har nedstrøms avskrådd lukebunn. Kapasitetskurve skal bestemmes i det lukeavløpet kan anses godt luftet og trykket ved luketerskelen når luken står stengt, er 37,0 mVS. For tunnelen forutsettes M = 33.
Manning: \[\Delta h = 3000\cdot c^2/(33^2\cdot 2,6^{4/3})=0,771\cdot Q^2/20^2=0,00193\cdot Q^2\qquad{(73)}\]
Kapasitet: \[Q = \mu\cdot å\cdot b\cdot a_{full}\cdot (2\cdot g\cdot (H-\mu\cdot å\cdot a_{full}-\text{konst}\cdot Q^2))^{0,50} \newline Q = \mu\cdot å\cdot 1,70\cdot 3,00\cdot (19,62\cdot (37-\mu\cdot å\cdot 3,00-0,00193\cdot Q^2))^{0,5} \newline Q^2 = (\mu\cdot å)^2\cdot 26,01\cdot (726-\mu\cdot å\cdot 58,9-0,0379\cdot Q^2) \newline Q = ((18900\cdot (\mu\cdot å)^2-1530\cdot (\mu\cdot å)^3)/1,986)^{0,5}\qquad{(74)}\]
Videre utregning av Q gjøres i tabell med Δå=0,2 og kontraksjonskoeffisienten μ hentet fra Figur 15. På grunnlag av dette kan siden kapasitetskurven tegnes.
| å | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
| LL | 0,625 | 0,630 | 0,675 | 0,740 | 0,950 |
| Q (m/s) | 12,3 | 24,8 | 40,2 | 59,1 | 96,2 |
13 Tapskoeffisienter for ventiler, rørbend, etc.
Tap i ventiler, rørbend etc. kalles singulærtap. De fleste uttrykkes ved: Δh = ζ•c2/2g.
![Figur 20: Tapskoeffisient ζ for rørbend med sirkulært strømningstverrsnitt [5].](/_resources/img/Vannkraft_Vannvei_Mekaniske-Konstruksjoner_Strømningsteknikk_img12p1.png)
Det vil i det etterfølgende føre for langt å gi fullverdig gjennomgang av alle ulike singulærtap. Som oppslagsbok kan man anbefale [5]. Figur 20 er eksempel på ett av de mange detaljerte og interessante diagrammer som er å finne i denne boken. Enkelte av de mest sentrale singulærtap refereres likevel nedenfor. Det understrekes at tapskoeffisientene er omtrentlige. For størstedelen er de hentet fra [5].
: Noen utvalgte singulære tap {#tbl:vannkraft_vannvei_mekaniske-konstruksjoner_strømningsteknikk-kraftverksvannvei_kap-12_utvalgte-tap}
Skarpkantet innstrømning til rør: Δh = 0,5•crør2/2g Avrundet innstrømning til rør: Δh = 0,1•crør2/ 2g Brå tverrsnittsutvidelse: Δh = (c1-c2)2/2g Sirkulært 90° avrundet bend: Δh = 0,16•crør2/2g 90° skarpkantet bend: Δh = 1,1•crør2/2g
Tapet i rørbend varierer med bendets krumningsradius. Best resultat for 90°-bend har man ved radius-diameter-forhold i området 2,0-3,5. Med radius menes da krumningsradien til rørets senterlinje. Årsaken til at tapet blir større når krumningsradien øker ut over angitt verdi, er at bendets lengde øker og at den vanlige rørfriksjonen da etter hvert blir det dominerende tapselement.
For bend med avbøyningsvinkel mindre enn 90°, kan det være en brukbar tilnærming å forutsette at ζ er proporsjonal med vinkelen.
Seriemonteres flere tapsgivende elementer nær hverandre i et rørsystem, kan totaltapet bli mindre enn summen av enkelttap. Er eksempelvis to 90°-bend montert i 4 rørdiametres innbyrdes avstand og slik at strømningsretning etter bendene er den samme som foran bendene, vil resulterende tap bli 70-80 % av deltapenes sum.
Ved rørforgreninger blir tapsforholdene kompliserte. Her bør en også være varsom med ukritisk bruk av håndbokdata. Som et eksempel kan man imidlertid referere et bukserør fra [5]. Dette er en symmetrisk forgrening hvor grenrørene er like og har samlet samme tverrsnitt som inngående rør. Hjørnene i rørforgreningen er avrundet. Tapet for strømningen til den ene rørgren uttrykkes ved: Δh = ζ•cinng2/2g. Som funksjon av vinkelen mellom grenrørene blir tapskoeffisienten ζ:
| Qgren/Qinng: | 0,20 | 0,40 | 0,60 | 0,80 |
| ζ60°: | 0,27 | 0,10 | 0,08 | 0,10 |
| ζ75°: | 0,28 | 0,14 | 0,10 | 0,12 |
| ζ90°: | 0,30 | 0,18 | 0,15 | 0,17 |
| ζ105°: | 0,39 | 0,24 | 0,22 | 0,24 |
Når det gjelder tap i åpne ventiler, kan man se bort fra tapet i kuleventiler. Dog må man være klar over at det ifm. ventiler kan være innsnevringer av rørdiameteren som medfører tap. For spjeldventiler gjengis fra 5 diagrammet i Figur 20, Sluseventiler har vanligvis tapskoeffisienter i området 0,15-0,2. Ifm. tilbakeslagsventiler blir spredningen av koeffisientverdier betydelig. Vanligvis ligger ζ mellom 1,0 og 3,0. Enkelte typer oppviser imidlertid ζ=0,5.
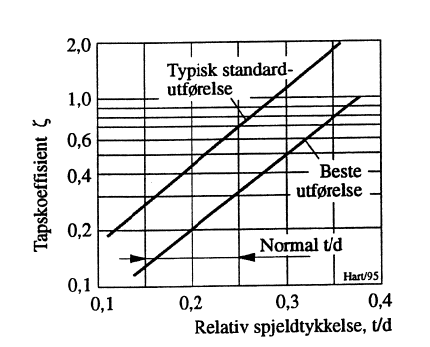
Forskjellen mellom tapskoeffisienter som man ved spjeldventilanskaffelse muligens kan håpe på å få, og det man risikerer å bli levert, er illustrert i Figur 21. Figuren taler for seg selv. Hva som er oppgitt av konkrete tapskoeffisienter fra enkelte større seriøse ventilleverandører, fremgår av Figur 22.
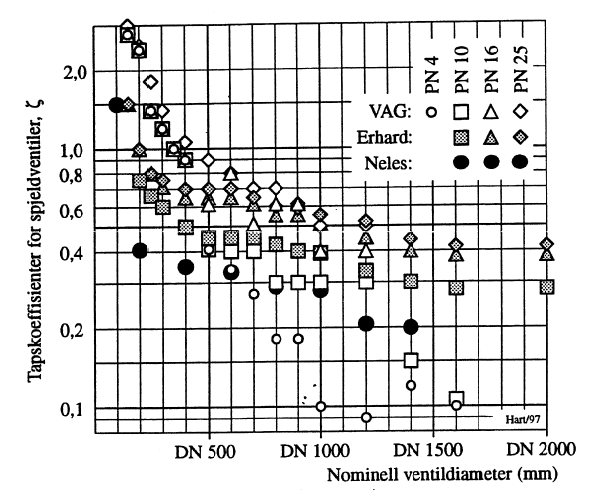
Tap i grinder beregnes med Kirchmers formel:
\[\Delta h = \zeta \cdot \text{sin}\beta\cdot (t/b)^{1,33}\cdot c^2/2g\qquad{(75)}\]
I formelen er β grindstavenes vinkel ift. strømningsretningen (vanligvis horisontalplanet), t grindstavtykkelsen, b lysåpningen mellom grindstaver og c strømningshastigheten foran grinden. For tapskoeffisienten ζ oppgir litteraturen data som angitt nedenfor. Vanligvis må man imidlertid påregne større tapskoeffisienter. For det første gjelder tapskoeffisientene staver i ren grind. Dessuten er det en forutsetning at innstrømmingen er parallell med grindstavene. Dette er ideelle forutsetninger som sjelden stemmer med virkeligheten.
| Flattstål, skarpe hjørner | ζ=2,42 |
| Flattstål, forkant og bakkant avrundet til halvsirkel | ζ=1,67 |
| Flattstål, forkant avrundet til halvsirkel, ineært avsmalende bakover til tykkelse t/2 | ζ=0,92 |
| Profil, formet som strømningsprofil | ζ=0,76 |
| Rundtstål | ζ=1,79 |
13.1 Eksempel
En varegrind står i inntaket til et kraftverkverksinntak som vist i Figur 23. Av grinddata som ikke fremgår av figuren nevnes: Stavtykkelse t = 12 mm, lysåpning mellom grindstaver 90 mm, stavene er laget av standard flattstål. For angjeldende grind skal det hydrauliske tapet bestemmes.
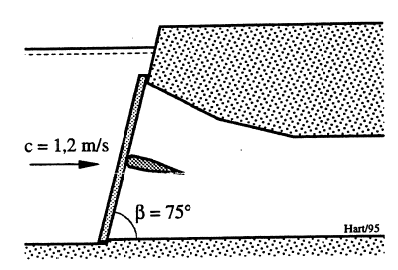
Det forutsettes at vannstrømningen inn mot grindstavene skjer i grindstavenes plan. Tapsfaktor hentes fra grindstavtabellen i Kapittel 13. Flattstål med skarpe hjørner har iht. denne ζ=2,42. Innsatt i Kirschmers formel får man:
\[\Delta h = \zeta \cdot \text{sin}\beta\cdot (t\cdot /b)^{1,33}\cdot c^2/2g \newline \Delta h = 2,42\cdot \text{sin}75^{\circ}\cdot (12/90)^{1,33}\cdot 1,2^2/19,62 = 0,012\space\text{mVs}\qquad{(76)}\]
13.2 Eksempel
Fra et reservoar A fører en 1000 m lang vanntunnel med tverrsnitt 12 m2 til et reservoar B. I avstand 200 m fra reservoar A er tunnelen tettet med betongpropp. Gjennom denne til et ventilkammer og gjennom ny betongpropp er det montert et Ø1600 mm rør med totallengde 40 m og på røret står det en DN 1600 spjeldventil som normalt er i åpen stilling.
For det tilfellet at høydeforskjellen mellom de to reservoarene er 24 m skal volumstrømmen gjennom systemet bestemmes.
Innledningsvis må alle faktorer som har betydning for tapene i systemet bestemmes/antas.
Ved innstrømningen til tunnelsystemet antas det et innløpstap med singulærtapskoeffisient 0,1. Uttrykt ved volumstrømmen Q blir dette tapet:
\[\Delta h_1 = 0,1\cdot 12^{-2}\cdot 19,62^{-1}\cdot Q^2=35\cdot 10^{-6}\cdot Q^2\qquad{(77)}\]
Tunnellengde er 1000-40=960 m. Hydraulisk diameter blir tilnærmet 120,5=3,46 m. Med referanse til kapittel settes ruheten lik 0,24 m. Prandtle-Nikuradses lov anvendes i det tunnelen anses som ru rør: λ = (2•lg(3,46/0,24) + 1,138)-2 = 0,088.
\[\Delta h_2 = 0,088\cdot (960/3,46)\cdot 12^{-2}\cdot 19,62^{-1}\cdot Q^2 = 8642\cdot 10^{-6}\cdot Q^2\qquad{(78)}\]
Ut fra tunnelen blir det et utløpstap. Dette tilsvarer hastighetshøyden i tunnelen.
\[\Delta h_3 = 12^{-2}\cdot 19,62^{-1}\cdot Q^2=354\cdot 10^{-6}\cdot Q^2\qquad{(79)}\]
Ved innstrømningen til stålrøret antas det innløpstap med singulærtapskoeffisient 0,2. Rørtverrsnittet er: π•1,62/4 = 2,01 m2. Tapet kan da skrives som:
\[\Delta h_4 = 0,2\cdot 2,01^{-2}\cdot 19,62^{-1}\cdot Q^2 = 2523\cdot 10^{-6}\cdot Q^2\qquad{(80)}\]
Tunnellengde er 1000-40=960 m. Hydraulisk diameter blir tilnærmet 120,5=3,46 m. Med referanse til kapittel settes ruheten lik 0,25 mm. Prandtle-Nikuradses lov anvendes i det røret anses å ha ideell ru strømning: λ = (2•lg(1600/0,25) + 1,138)-2 = 0,013.
\[\Delta h_5 = 0,013\cdot (40/1,60)\cdot 2,01^{-2}\cdot 19,62^{-1}\cdot Q^2 = 4100\cdot 10^{-6}\cdot Q^2\qquad{(81)}\]
Fra røret ut i tunnelen blir det et impulstap ved overgang fra 2,01 m2 tverrsnitt til 12 m2. Dette tapet uttrykkes som:
\[\Delta h_6 = (2,01^{-1}-12^{-1})^2\cdot 19,62^{-1}\cdot Q^2 = 8743\cdot 10^{-6}\cdot Q^2\qquad{(82)}\]
For ventilen antas det med referanse til Figur 21 en singulærtapsfaktor på 0,4:
\[\Delta h_7 = 0,4\cdot 2,01^{-2}\cdot 19,62^{-1}\cdot Q^2= 5046\cdot 10^{-6}\cdot Q^2\qquad{(83)}\]
Summen av tapene må tilsvare systemets drivende trykk som er nivåforskjellen mellom reservoarene. Dette gir en ligning hvorav volumstrømmen kan løses.
\[24 = (35+8642+354+2523+4100+8743+5046)\cdot 10^{-6}\cdot Q^2 \newline Q = (24\cdot 10^6/29443)^{0,5}= 28,6\space \text{m}^3\text{/s}\qquad{(84)}\]
14 Vannstandsprang
Strømningen ut fra et tappeanlegg kan ha stor hastighet. Er avløpet åpen kanal eller luftet tunnel, blir det vesentlig om hastigheten er større enn overflatebølgers forplantnings- hastighet. I så fall sier en at strømningen er overkritisk.
Med x definert som strømningens dybde blir forplantningshastigheten for en overflatebølge cbølge=(g•x)0,5. Ut fra dette er forholdet mellom strømningshastighet og bølgeforplantningshastighet definert som et dimensjonsløst tall, Froudes tall, Fr. Vilkåret for overkritisk strømning blir følgelig: Fr = c/(g•x)0,5 > 1
Det gjøres imidlertid oppmerksom på at det i faglitteraturen også forekommer et Froude- tall definert som kvadratet av det forannevnte.
For enhver dybde x1 med overkritisk strømning har man også en tilhørende (konjugert) dybde x2 med underkritisk strømning hvor Fr < 1. Forholdet x1/x2 beregnes vha. impuls- og kontinuitetsligningen.
\[x_2/x_1 = 0,5\cdot ((1+8\cdot Fr_1^2)^{0,5}-1)\qquad{(85)}\]
Overgangen fra overkritisk til underkritisk strømning skjer i en stående bølge, vannstand- sprang. Dette følges av et hydraulisk tap som iht. Bernoullis ligning blir:
\[\Delta h_{sprang} = c_1^2/2g + x_1 - c_2^2/2g-x_2\qquad{(86)}\]
Stedet hvor vannstandsprang opptrer, kan det være av betydning å kunne bestemme. At man i praksis ofte ser at vannstandsprang utløses ved redusert kanalhelning, kan forklares som angitt nedenfor.
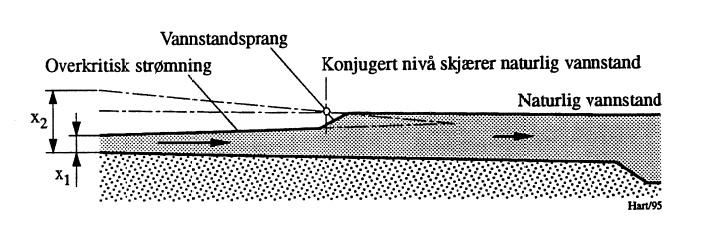
For aktuell volumstrømmen har en kanal en “naturlig” strømningstilstand. Denne gis av kanalhelningen og eventuelt et vann-nivå etter kanalen. Den overkritiske strømningen i kanalens oppstrøms ende er utsatt for friksjonstap og vil dersom kanalhelningen ikke er for stor, etter hvert bli redusert. Ved dette øker dybden x1 samtidig som den konjugerte størrelse x2 reduseres. Er kanalens naturlige strømningstilstand underkritisk, inntreffer vannstandspranget der den konjugerte vannstand blir lik den naturlige. I motsatt tilfelle fortsetter strømningen som overkritisk, kanalen ut. Forholdet er illustrert i Figur 24. Praktiske beregninger gjennomføres trinnvist langs kanallengden og kan med fordel gjøres i regneark.
Mer komplisert blir forholdet når vannstandspranget skjer i en tunnel hvor den underkritiske strømningen etter spranget fyller hele tunneltversnittet. Denne situasjon er beskrevet i [8] for tunnel med rektangulært tverrsnitt. Settes trykket ved kanalbunnen etter vannstandspranget lik h2 samtidig som tunneltverrsnittets høyde er Htun og Φ = x1/Htun, blir:
Sprangligningen: \[h_2/x_1 = 0,5\cdot (\Phi+\Phi^{-1})+Fr_1^2\cdot (\Phi - \Phi^2)\qquad{(87)}\]
Tapet: \[\Delta h_{sprang} = c_1^2/2g + x_1-c_2^2/2g-h_2\qquad{(88)}\]
14.1 Eksempel
Det er vannstandsprang i en kanal med bredde 2,0 m og volumstrøm 15,0 m3/s. Oppstrøms vannstandspranget er hastigheten 8,5 m/s. Strømningsdybden etter vannstandspranget skal fastlegges sammen med falltapet.
Oppstrøms dybde: \[x_1 = Q/(c_1\cdot b) = 15,0/(8,5\cdot 2,0) = 0,882\space\text{m}\qquad{(89)}\]
Froudes tall: \[Fr_1 = c_1/(g\cdot x_1)^{0,5}=8,5/(9,81\cdot 0,882)^{0,5}=2,89\qquad{(90)}\]
Nedstrøms dybde: \[x_2 = x_1\cdot (0,5\cdot ((1+8\cdot Fr_1^2)^{0,5}-1)) \newline x_2= 0,882\cdot (0,5\cdot ((1+8\cdot 2,89^2)^{0,5}-1)) = 3,19\space\text{m}\qquad{(91)}\]
Nedstrøms hastighet: \[c_2 = Q/(x_2\cdot b)=15,0/(3,19\cdot 2,0)=2,35 \space\text{m/s}\qquad{(92)}\]
Falltap: \[\Delta h_{sprang}=c_1^2/2g+x_1-c_2^2/2g-x_2 \newline \Delta h_{sprang}=8,5^2/(2\cdot 9,81) + 0,882-2,35^2/(2\cdot 9,81)-3,19 = 1,09\space\text{mVs}\qquad{(93)}\]
15 Kavitasjon
Kavitasjon oppstår i en væskestrøm når trykket underskrider væskens damptrykk. Dette er temperatureavhengig.
| Temperatur: | 0 °C | 10 °C | 20 °C | 30 °C |
| Fordampningstrykk [3]: | 6 mbar | 12 mbar | 23 mbar | 42 mbar |
Ved kavitasjon dannes det dampblærer som følger væskestrømmen. Når blærene kommer til et område hvor trykket er større enn fordampningstrykket, kollapser de. Skjer dette mot en stål- eller betongoverflate, utsettes denne for kavitasjonstæring.
Det er strømningsteknisk to ulike metoder som motvirker kavitasjonstæring. Den tradisjonelle har vært å sørge for at trykket overalt ligger så høyt at kavitasjon, dannelsen av dampblærer, ikke inntreffer. Et mindre vanlige alternativ blir å holde trykket langs de flater hvor tæringer er uønsket, så lavt at dampblærene her ikke gis anledning til å kollapse.
Vurdering av om kavitasjon kan oppstå, gjøres vha. konstruksjonens kritiske kavitasjons- parameter σcr. Denne er:
\[\sigma_{cr}=2\cdot (p_{cr}-p_d)/(\rho\cdot c_{cr}^2)\qquad{(94)}\]
I formelen er pcr høyeste trykk i hovedstrøm som gir kritisk kavitasjon, pd damptrykket, ρ væskens densitet og ccr hastighet i hovedstrøm som korresponderer med pcr. Ofte presenteres imidlertid formelen på forenklet form i det pd settes tilnærmet lik absolutt vakuum, p lik omgivelsestrykket og c2/2g=H. Som resultat får man da:
\[H \space<\space 10/\sigma_{cr}\qquad{(95)}\]
For luker med føringsnisjer og godt luftet avløp blir vanligvis området like etter føringsnisjene mest utsatt for kavitasjonstæring. Ved overslagsberegninger ifm. skarpkantede rektangulære føringsnisjer antyder [8] 0,8 som passende verdi for σcr. Det opplyses også at tilbaketrukket nedstrøms føringshjørne kan redusere σcr til nærmere 0,1.
![Figur 25: Nødvendig mottrykk nedstrøms dykket tappeorgan [8].](/_resources/img/Vannkraft_Vannvei_Mekaniske-Konstruksjoner_Strømningsteknikk_img14p1.png)
Har tappeorganet dykket avløp slik at strømningen her ikke vil kunne stabiliseres ved tilførsel av luft, kan det i strålesonen oppstå betydelige kavitasjons- og pulsasjonsproblemer. Dette har bl.a. sammenheng med tverrsnittsutvidelsen fra tappetverrsnitt til nedstrøms vannvei. Her anbefaler NHL [8] en kavitasjonsparameter satt til 0,8. Forskere ved et par internasjonalt prøvelaboratorier har imidlertid foreslått 0,6 som grense.
Beregninger utført ved NHL av luker med dykket avløp gir sammenhengen mellom effektiv fallhøyde for et tappeorgan, mottrykk, forholdet tappeåpning/tunneltverrsnitt å•A1/A2 og kavitasjonsparameter σ [8]. Dette gjengis i Figur 25 for σ=0,8 og σ=0,6.
En spesiell kavitasjonsparameter er σi. Denne angir begynnende kavitasjon representert ved utskillelse av luft i undertrykksområdene. Det antydes [8] at σi er anslagsvis 3 ganger større enn σcr.
16 Massesvingninger i vannveien
Massesvingninger oppstår ved ikke-stasjonære strømningsforhold som eksempelvis oppstår når turbin, luke eller ventil blir manøvrert. Det vanlige er at forholdet kartlegges ved en trinnvis beregning langs tidsaksen med Newtons kraftligning og kontinuitetsligningen. Ved dette anses vann og rør som stive elementer. Det tas således ikke hensyn til virkningen av elastiske trykkbølger som vil bli behandlet i det etterfølgende kapittel.
Uelastisk betraktning av trykkvariasjonene i en vannstreng kan gi tilstrekkelig nøyaktighet når tiden for vannføringsendringen er meget lang i forhold til bølgeforplantningstiden i vannstrengen. Som regel er det også slik at transiente trykkforhold i vanntunneler anses bestemt av vann-nivået i svingesjakter, hvilket løses med “uelastisk” teori. For trykkvariasjonene i tilløpsrør blir det derimot viktig at det tas hensyn elastiske trykkbølger.
Viktigste ligning ved uelastiske forhold er som tidligere nevnt Newtons ligning. Denne omdannes til “differensiell” form med et kort tidsintervall Δt som angitt nedenfor.
Newtons ligning: Kraft = masse • akselerasjon
Omformet for tunnel: Δh = (l/g) • ltunnel • (Δc/Δt)
Hvordan en beregning i praksis kan gjennomføres, fremgår av Kapittel 16.1. Dette eksemplet behandler forholdene i et kraftverks tilløpssystem, men kartleggingen av hva som skjer i av-løpssystemet, blir som regel minst like viktig. Her har man vanligvis en sugerørslukesjakt som danner åpen forbindelse mellom avløpssystemet og kraftstasjonshallen. Det er viktig at massesvingninger ikke kan medføre at vann strømmer opp gjennom sugerørslukesjakten slik at det flommer over i denne og drukner kraftverket. En annen uheldig mulighet kan dessuten være at vann-nivået synker så meget at uønsket luft trekkes inn i vanntunnelsystemet.
Skal forhold av nevnte type kartlegges, må man imidlertid bestemme seg for om det skal regnes en eller flere vannføringsendringer etter hverandre. Foretas det flere manøvreringer ved ugunstige tidspunkter, kan grensene for opp- og nedsving som følge av en manøvrering, i vesentlig grad bli overskredet/underskredet.
16.1 Eksempel
En kraftverk har oppstrøms vannvei med hydraulisk utforming som vist i Figur 26. Nederst i svingesjakten er det et strupende tverrsnitt As.
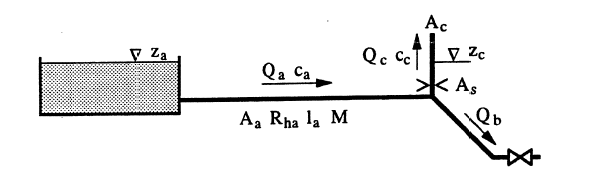
Aktuelle dimensjoner:
Tilløpstunnel: Aa=20 m2, la=2000 m, za=50,0 m, M =33.
Svingesjakt: Ac=12 m2, As=2 m2.
Stasjonære vannføringer: Qa0=25 m3/s, Qb0=25 m3/s, Qc0=0 m3/s
Turbinens stengetiden er 6 sekunder. Turbinvannføringen avtar da lineært til 0 m3/s. For dette tilfellet skal høyeste nivå ved første oppsving i svingesjakten bestemmes som funksjon av tiden. Algoritmer for trinnvis tilnærmet beregning i regneark når det forutsettes lite tidsintervall Δt, gjengis nedenfor.
Kontinuitet ved tidspunkt t: \[Q_{at}=Q_{bt}+Q_{ct}\qquad{(96)}\]
Oppstrømning i sjakt fra (t-1) til t: \[z_{ct}=z_{c(t-1)}+Q_{c(t-1)}\cdot \Delta t/A_c\qquad{(97)}\]
Tunneltap ved tidspunkt t: \[\Delta h_{at}=Q_{a(t-1)}^3\cdot l_a/(|Q_{a(t-1)}|\cdot M^2\cdot R_{ha}^{1,33})\qquad{(98)}\]
Tap i strupe ved tidspunkt t: \[\Delta h_{ct} = Q_{c(t-1)}^3/(|Q_{c(t-1)}|\cdot 2\cdot g\cdot A_s^2)\qquad{(99)}\]
Retarderende / aksellererende trykk: \[\Delta h_t = z_{ct} + \Delta h_{at}+\Delta h_{ct}-z_a\qquad{(100)}\]
Newtons lov for tilløpstun., omformet: \[\Delta c_{at} = \Delta h_{(t-1)}\cdot \Delta t\cdot g/l_a\qquad{(101)}\]
Vol.strøm i tilløpstunnel ved tidspkt.t: \[Q_{at} = Q_{a(t-1)}-\Delta c_{at}\cdot A_a\qquad{(102)}\]
Beregningsresultat med Δt=0,5 sekund blir:
| Tid (s) | Vannst. (moh) |
|---|---|
| 0 | 47,7 |
| 3 | 49,0 |
| 6 | 53,2 |
| 9 | 58,5 |
| 12 | 62,7 |
| 15 | 65,7 |
| 18 | 67,4 |
| 21 | 67,8 |
| 24 | 66,9 |
| 27 | 64,8 |
| 30 | 61,8 |
17 Trykkstøt
Trykkstøt kan opptre sammen med massesvingninger. En trykkstøtsberegning vil primært bli aktuell når det er tale om lange, lukkede og fylte vannveier. Tidspunktene for maksimalt trykkstøt og maksimal massesvingning er svært ulike.
Trykkstøtsberegninger utføres vha. bølgeligninger bestående av bevegelsesligningen og kontinuitetsligningen. Begge har ikke-stasjonære ledd og kan løses ved hjelp av karakteristikkmetoden. Dette forutsetter at rørsystemet deles i små rørelementer med lengde Δv, referert til et meget kort og konstant tidsintervall Δt samt til trykkbølgehastigheten a slik at Δx = a•Δt. For et punkt D som ligger Δx nedstrøms punkt A og Δx oppstrøms punkt B vil pietzometertrykk hpD og volumstrøm QD kunne beregnes ved tidspunkt t1+Δt når tilsvarende trykk og volumstrøm er kjent for punktene A og B ved tidspunktet t1. Ligningene for dette gjengis ved etterfølgende ligningspar samt ved Figur 27 som gjengir beregningsgangen.
\[h_{pD}- h_{pA} + (a/(g\cdot A)) \cdot (q_D-q_A)+k\cdot q_A\cdot |q_A| =0 \newline h_{pD}- h_{pB} + (a/(g\cdot A)) \cdot (q_D-q_B)+k\cdot q_B\cdot |q_B| =0\qquad{(103)}\]
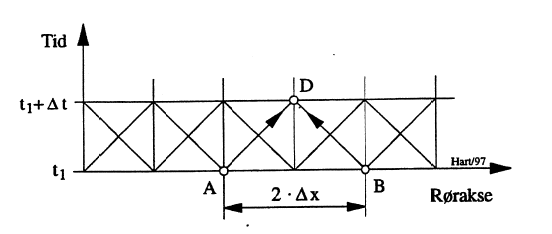
Som det fremgår av det forannevnte, vil trykkstøtsberegning etter karakteristikkmetoden gi trykk og volumstrøm ved alle rørelementer med lengde dx for tider med innbyrdes intervall At.
Et kompliserende forhold ved trykkstøtsberegninger er volumstrømfunksjonen. Har man en ventil som stenger, bør det ved beregningen tas hensyn til at trykkstigningen øker vannføring gjennom ventilen. Er det en Francis-turbin som utsettes for avslag, blir det en turtallsøkning som kan virke bremsende på vanngjennomstrømningen. En viktig forskjell mellom egnede og mindre egnede dataprogrammer for beregning av trykkstøt, er hvordan regneprogrammene tar hensyn til nevnte forhold.
Fra tiden før datamaskiner ble tatt i bruk for trykkstøtsberegninger eksisterer det også en grafisk løsningsmetode. I denne sammenheng benyttet man en forenklet utgave av bølgeligningene, Allievis ligninger. Disse kan for ukompliserte vannveisystemer løses grafisk. Metoden er beskrevet av professor Brekke i hans forelesningskompendium “Regulering av hydrauliske strømningsmaskiner” [1].
En ytterligere forenkling av trykkstøtproblematikken kan forutsette momentan vannføringsendring skjer. For dette tilfellet blir løsningen av bølgeligningene mindre komplisert og forbindes vanligvis med navnet Joukowsky. Aktuell trykkendring forårsaket av momentan vannføringsendring er:
\[\Delta p = \rho \cdot \Delta c\cdot a\hspace{1cm} \text{eller} \hspace{1cm} \Delta h = \Delta c\cdot a / g= \Delta Q\cdot a/(g\cdot A)\qquad{(104)}\]
Når det gjelder a, trykkbølgehastigheten i vannveien (lydhastigheten) kan denne variere betydelig, avhengig av forholdene. Forutsettes det stivt rør og rent vann, blir nevnte hastighet rundt 1500 m/s. I tuneller med godt fjell og innstøpte stålforinger når luftinnblandingen i vannet er svært liten, kan det forutsettes å = 1000 - 1200 m/s. For frittliggende rør, særlig plastrør og trerør hvor elastisiteten er stor, kan derimot hastigheten komme ned i 500 - 600 m/s. Ønsker man mer eksakt bestemmelse av trykkbølgehastigheten, kan dette for rør gjøres ved hjelp av formelen:
\[a = \sqrt{\frac{K\cdot E\cdot s}{\rho\cdot E\cdot s + \rho\cdot K\cdot d\cdot (1-\mu^2)}}\qquad{(105)}\]
d: Rørdiameter (m)
s: Rørveggens tykkelse (m)
E: Rørets E-modul (Pa) (Estål=204•109 Pa og EGUP=15•109-30•109 Pa)
K: Vannets volumelastisitet (Pa) (ca. 2,3•109 Pa [4] uten luftinnblanding)
μ: Poissons tall for rørmaterialet (μstål=0,3)
ρ: Vannets densitet (kg/m3) (ρvann=1000 kg/m)
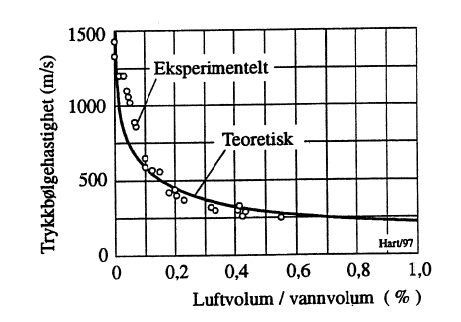
Som det fremgår, kan vannets volumelastisitet ha vel så stor betydning for trykkbølge- hastigheten som rørmaterialets elastisitetsmodul. Det som i denne sammenheng kan innvirke på volumelastisiteten, er luftinnblanding i vannet. Referert til [5] gjengir Figur 28 luftinnblandingens betydning.
Når en ventil i et rørs nedstrøms ende stenger, vil det gå en trykkbølge fra ventilen, opp røret. Har dette lengde L, når trykkbølgen rørets oppstrøms ende ved tiden T = L/a. Som sterkt forenklet regneregel kan det da hevdes at trykkøkningen tilsvarer Joukowsky- trykkstøtet hvis ventilens stengetid Tvent er mindre enn 2L/a. Har man derimot Tvent vesentlig større enn 2L/a og dQ/dt konstant kan det for “romslige” overslagsberegninger ved første trykktopp forutsettes:
\[\text{Ved }T_{vent} >> 2L/a: \Delta h = (\Delta Q\cdot a/(g\cdot A))\cdot (2\cdot L/(a\cdot T_{vent}))\newline \Delta h = 2\cdot \Delta Q\cdot L/(g\cdot A\cdot T_{vent})\qquad{(106)}\]
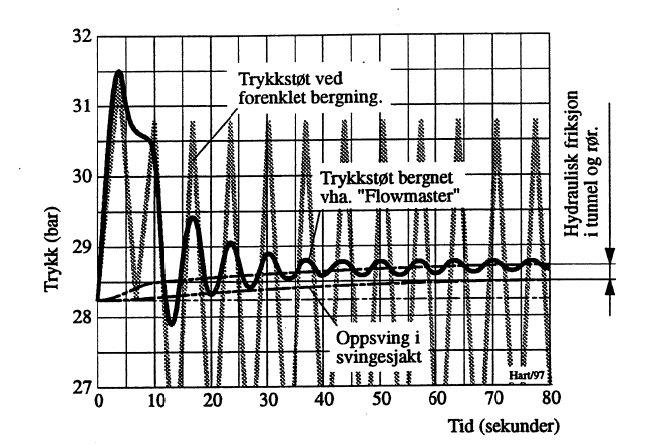
I flere tilfeller hvor stengetiden var mer enn 8 ganger refleksjonstiden, 2L/a, har de tilnærmede metode gitt forholdsvis god overenstemmelse med mer pålitelige fastleggelser av trykkstøtets størrelse. Et eksempel på dette gjengis i Figur 29 hvor trykkstøt i et kraftverk med Pelton-turbin er beregnet både forenklet og med dataprogrammet “Flowmaster”.
Et annet tilfelle er gjengitt i #sec:vannkraft_vannvei_mekaniske-konstruksjoner_strømningsteknikk-kraftverksvannvei_kap-16_kap16-1. Dette refererer til et anlegg med Francis-turbin uten frekvensregulator og med øvrige data som angitt. Ved avslagsprøve ble maksimalt trykk ved fullastavslag målt til 82 m. Overenstemmelsen mellom forenklet beregning og praktisk prøve er imidlertid langt større enn det man på forhånd kunne ha forventet, se avsluttende bemerkninger angitt i eksemplet.
17.1 Eksempel
Et kraftverk er utstyrt med Francis-turbin og GUP-rør. Turbinens lukketid ved fullastavslag er 22,5 s. Fullastvannføringen kan settes lik 4,46 m3/s. Tilløpsrøret har innvendig diameter Ø1150 mm og lengde 300 m. Trykkstøt kan med nevnte størrelser beregnes i henhold til foran angitte formel for overslagsberegninger underforutsetning av at vannføringen endres lineært under lukketiden:
Rørtverrsnitt: \[A = \pi\cdot d^2/4 = \pi\cdot 1,150^2/4=1,039 \space\text{m}^2\qquad{(107)}\]
Trykkøkning: \[\Delta h = 2\cdot \Delta Q\cdot L /(g\cdot A\cdot T_{vent})\newline =2\cdot 4,46\cdot 300/(9,81\cdot 1,039\cdot 22,5)=11,7\space\text{m}\qquad{(108)}\]
Det forutsettes at veggtrykket foran turbinen, før avslaget, er 62,5 m, mens statisk trykk samme sted etter avslaget blir 70,5 m. Antas det at maksimaltrykket opptrer mot slutten av lukkesekvensen da hastigheten i røret er nær 0 m/s, blir maksimaltrykket:
\[H_{maks}=H_{stat}+\Delta h=70,5+11,7=82,2\space\text{m}\qquad{(109)}\]
Det må dog understrekes at forutsetning at størrelsen dQ/dt blir konstant under lukkesekvensen er en grov forenkling. I virkeligheten vil turbinen ved avslaget gå til rusning og ved dette skape ekstra mottrykk som virker bremsende på vannføringen. Dette medfører i neste omgang kraftigere retardasjon av vannstrengen og følgelig økt trykkstøt. På den annen side kommer maksimal trykkøkning nå på et tidspunkt hvor det fortsatt er friksjonstap i rørsystemet slik at Hstat da er litt lavere enn den verdi det foran er regnet med.
18 Hydrauliske resonanser i tunnelsystemer
Før 1970 var kontroll mot det såkalte Thoma-kriteriet eneste resonanskontroll ved kraftverk. Etter denne tid har man tatt i bruk Bode-Nyquists metode som gjennom mange år har vært velkjent blant elektroingeniører med reguleringsteknisk bakgrunn. For ikke-spesialister kan den derimot bli vanskelig å forstå. Beregningsresultatene beskriver eksempelvis ikke aktuelle hendelser i tidsplanet, men konsentreres om hvordan ørsmå oscillerende forstyrrelser påvirkes i det dynamiske systemet som et vannkraftanlegg er.
Det kan ellers hevdes at nevnte forhold i liten grad angår de maskintekniske installasjonene oppstrøms og nedstrøms kraftverkets hydrauliske maskiner. Dog bør en være klar over at fysiske egenskaper til selv statiske konstruksjoner som tilløpsrør, kan bli av betydning for et kraftverks reguleringsstabilitet. Ved ethvert inngrep som kan bidra til å
endre resonansene i vannveien, bør derfor relevant ekspertise tas i bruk slik at virkningene allerede på planleggingsstadiet blir kartlagt. Dessuten er det selvsagt også slik at om resonanser fra massesvingninger og trykkstøt gis anledning til å bygge seg opp, vil dette bl.a. kunne medføre rørbrudd.
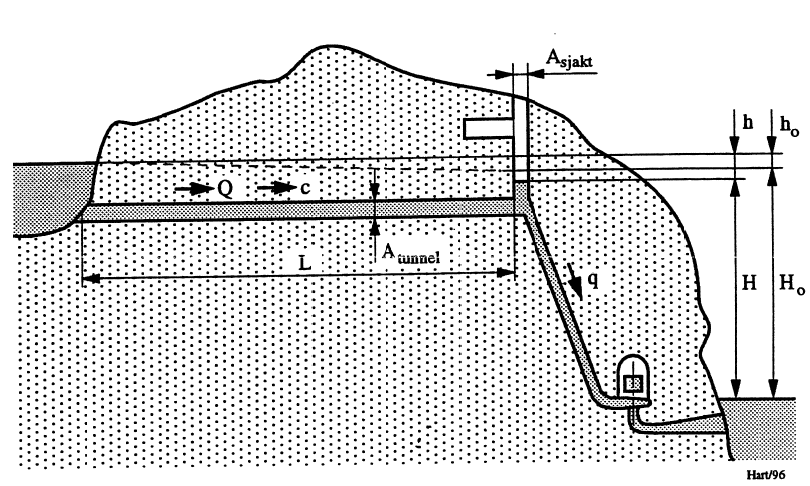
Som nevnt sto tidligere Thoma-kriteriet svært sentralt ved vurdering av kraftverksstabilitet. Fortsatt har det også stor betydning ved overslagsberegninger. Med henvisning til størrelser som angitt i Figur 30, kan nevnte stabilitetsbetingelse uttrykkes ved:
\[\text{Stabilitet når}:\hspace{1cm} A_{sjakt}>1,5\cdot \frac{L\cdot A_{tunnel}\cdot c_o^2}{2\cdot g\cdot h_o\cdot (H-h_o)}\qquad{(110)}\]
Anvendelsen av en enkel betingelse som den angitte, kan synes uproblematisk. En bør likevel være klar over at uttrykket matematisk forteller at det alltid vil være behov for svingesjakt, uansett tunnellengde og tverrsnitt. Praktisk erfaring tilsier at det ikke er tilfelle.
Ut over dette bør en også være klar over at Thoma-kriteriet kun tar hensyn til masse- svingningene i vannveiene. Det er likevel også mange andre forhold som kan gi opphav til uheldige resonanser og som det bør tas hensyn til. Viktig i denne sammenheng blir eksempelvis refleksjonstidene for elastiske trykkstøt. Et sett forenklede stabilitetsbetingelser som tar hensyn til dynamiske forhold ved roterende masser og den delen vannveien som er mellom svingesjakt og turbin, kan dessuten siteres fra professor Hermod Brekke, se referanse [1].
| Betingelse - 1 | Betingelse - 2 |
|---|---|
| Ta/Tw ≥ 5,0 | 0,3 < hw < 0,5 |
| Ta/Tw ≥ 4,0 | 0,5 < hw < 0,7 |
| Ta/Tw ≥ 3,5 | 0,7 < hw < 1,0 |
| Ta/Tw ≥ 3,0 | 1,0 < hw < 2,0 |
| Ta/Tw ≥ 2,0 | 2,0 < hw |
Tabell 12 gir definisjoner av tidskonstantene i Tabell 11
| Konstant | Definisjon |
|---|---|
| Aggregatets aksellerasjonstid | Ta = (π•*n/30)2•J/°P |
| Vannveiens aksellerasjonstid | Tw = S/(g•Hn) |
| Allievis konstant | hw = a•c/(2•g•Hn) |
| Sum | S = Σ(Q•L/A) |
| Aggregatets treghetsmoment | J = GD2/4 |
| Netto fallhøyde | Hn |
| Turbinens fullasteffekt | °P |
19 Avløsningsvirvler
Avløsningsvirvler kan oppstå på flater som bøyer bort fra en vannstrøm eller bak kanter som står i vannstrømmen. Virvlene gir opphav til trykkpulsasjoner med påfølgende utmattingseffekt. Forholdet kan kartlegges vha. kompliserte regneprogrammer som løser Navier Stokes ligninger, de generelle strømningsligningene. Det vanligste er imidlertid at man benytter eksperimentaldata sammen med erfaringer og sørger for å utforme konstruksjonene slik at skadelige avløsningsvirvler ikke oppstår. Konstruksjoner hvor avløsningsvirvler har gitt opphav til problemer, er varegrinder, høytrykks tappeluker og sektorluker.
For varegrinder er det aktuelt å sammenligne virvelfrekvens med grindkonstruksjonens egensvingefrekvens. Strømningstekniske del av slik beregning består i bestemmelse av virvelfrekvensen. Denne finnes vha. Strouhals tall (St). For avløpet ved en grindstav har mange ved slik beregning lagt til grunn et Strouhals-tall i området 0,19 - 0,20. Referanse [8] som for samme anvendelse kan indikere at St = 0,12, blir i denne sammenheng mindre relevant. På den annen side kan skjevstrømninger og mulig ujevn hastighetsfordeling, slik man særlig risikerer ved større grinder, tilsi at man bør forutsette Strouhals-tall innen området 0,10 - 0,30.
\[\text{Vivelfekvens for staver i varegrind}:\hspace{1cm} f = St\cdot c/t_{stav}\qquad{(111)}\]
20 Luftutblåsninger
Luftutblåsninger kan opptre ifm. lukkede dykkede vannveier hvor luft trekkes inn i systemet og samles i lommer inntil mengden blir så stor at den kan unnvike ved utstøtning gjennom eksempelvis en sjakt. Luftutblåsninger har vært årsak til betydelige havarier ved norske kraftverk.
21 Hydrauliske målinger
Feltmålinger som skal gjennomføres med nevneverdig nøyaktighet, er som regel ikke bare kompliserte, men også omkostningskrevende. Selv falltapsmålinger hvor det er tale om trykkregistreringer i to tverrsnitt, kan være problematiske. I denne forbindelse fremheves:
Måletverrsnittenes areal må være kjent.
Midlere hastighetshøyde er ikke nødvendigvis lik: (cm)2/2g
Anvendte trykkuttak kan gi bidrag fra hastighetshøyden pga. feil orientering, stående virvler eller sekundærstrømmer.
Trykkpendlinger i vannsystemet gir usikre avlesninger.
Måletverrsnittene kan være ugunstig plassert ift. det man ønsker å måle falltapet over.
Er det eksempelvis aktuelt ved falltapsmåling av et kraftverksrør å bestemme rørets ruhet som er en viktig tilstandsstørrelse, kan følgende tenkte forhold nevnes til illustrasjon av enkelte av de forannevnte punkter: Trykket foran røret måles ved peiling av vannstanden i en sjakt. Her er det hele tiden mindre pendlinger. En stående virvel nederst i sjakten kan for målingen være feilkilde. Her har man også for tunnelprofilet kun de teoretiske sprengningsdimensjonene å forholde seg til. Etter måletverrsnittet er det montert varegrind. Singulærtapet for denne har man ingen mulighet til å få målt. Det samme gjelder singulærtapene for kraftverksrørets bend. Nedre måletverrsnitt ligger kloss opp i nedre rørbend. Her influeres trykkmålingene av sekundærstrømmene fra bendet.
Vannføringsmålinger blir som regel de av de hydrauliske feltmålinger som innebærer størst usikkerhet. Ulike metoder er aktuelle:
Volumetriske målinger: Over en viss tid tappes det med konstant åpningsgrad på tappeanlegget. Siden måles nivåforskjell i det magasin det er tappet fra. Forskjellen bør være neglisjerbar i forhold til trykkfallet over tappesystemet. Man må dessuten ha kontroll med eventuelt tilsig.
Hastighetsmålere (flygler, etc.): I et definert tverrsnitt måles strømningshastigheten i ulike målepunkter. Siden integreres hastigheten over tverrsnittet. Bjelkestengselføringer kan her være egnede fordi tverrsnittet er veldefinert samtidig som hastighetsmålerne kan monteres på en ramme tilpasset føringen. Traverseringen av tverrsnittet gjennomføres ved heising/firing av rammen.
Sporstoffmålinger: Disse avløser tidligere salthastighets- og saltoppløsningsmetode. Problemet er at sporstoffet må blandes jevnt i det vann som strømmer gjennom lukeløpet, hvis ikke vil nedstrøms konsentrasjonsmålingen avhenge av hvor prøven blir tatt og eventuelt gi misvisende resultat.
Ultralydmåling: Metoden forutsetter at man har et definert måletverrsnitt og at man i dette får montert en rekke ultralydsensorer. Aktuelt antall kan være 8-16 sensorer med 4-8 målebaner.
Turbin: For de fleste turbiner er virkningsgraden kjent. Har man et arrangement som er slik at vannføringen som ønskes målt, går gjennom en turbin, kan denne forholdsvis enkelt benyttes som vannføringsmåler.
Usikkerheten ved volumstrømmåling varierer fra metode til metode. Ultralydmålinger utført under ideelle forhold skal riktignok kunne gi resultater ned mot ± 0,5 %. Stort sett kan det imidlertid hevdes at det under feltforhold er vanskelig å få mindre usikkerhet enn ± 3-5 %.
IEC-Publication 41 [12] gir råd og anbefalinger som med tanke på feltmålinger kan være nyttige. Selv om dokumentet i hovedsak er rettet mot virkningsgradsbestemmelse for hydrauliske maskiner, kan det også anses som et dokument med generell gyldighet.
Et forhold som det avslutningsvis må understrekes viktigheten av, er at alt måleutstyr skal være identifisert og kalibrert iht. aksepterbare rutiner. Etter at målinger er utført og bearbeidet bør det også alltid inngå en vurdering og kvantifisering av aktuell usikkerhet. ’ Vanlig prosedyre er at resulterende usikkerhet beregnes som kvadratroten av delbidragenes kvadratsum. For volumstrømmåling med overfall vil dette eksempelvis bli:
\[\text{Resulterende usikkerhet =}\space (X_1^2 + X_2^2 + 1,5^2\cdot X_3^2)^{0,5}\qquad{(112)}\]
Her er X, usikkerhet knyttet til hastighetsprofilet ved tilstrømningen til overfallet samt til overfallets avløpsfaktor. X> blir usikkerhet ifm. overløpets bredde, og X3 er usikkerheten ifm. høydeforskjellen fra overfallets bunn til oppstrøms vannstand.
22 Modellmålinger
Stilles det strenge krav til en kapasitetskurves nøyaktighet, har denne tradisjonelt blitt bestemt ved modellmåling. Generelt krav er da at det skal være hydraulisk likedannethet mellom modell og prototyp. For lukestrømning blir to dimensjonsløse tall sentrale:
| Reynolds tall: | Re = treghetskrefter / viskøse krefter = | c•x/v |
| Froudes tall: | Fr = treghetskrefter / tyngdekrefter = | c2/(g•x) |
| For åpen kanal: | Fr = strømn.hastighet / bølgehastighet = | c/(g•x)0,5 |
Symboler:
- c: hastighet
- g: gravitasjonskonstanten
- x: karakteristisk lengde
- ν: kinematisk viskositet
Likhet fra modell til prototyp for både Reynolds tall og Frouds tall kan man kun få når den lineære skalafaktor y er 1. Man må derfor i det enkelte tilfelle konsentrere seg om det dimensjonsløse tall som har størst betydning for strømning. Ved strømning gjennom dykket luke vil eksempelvis Reynolds-tallet være det viktigste. Froudes tall har mest å si for luker hvor det er frispeilstrømning. i
Modell-lovene blir forskjellige avhengig av om strømningen er Reynold- eller Froudedominert. For en “Froude-modell” og en “Reynold-modell” hvor lineær-skalaen i begge tilfeller er y, blir skalaene for trykk og vannføring:
| “Froude-modell”: | Hm/Hp = y | Qm/Qp = y2,5 |
| “Reynold-modell”: | Hm/Hp = y-2 | Qm/Qp = y |
For “Reynold-modeller” aksepteres det imidlertid vanligvis at man har modelloverenstemmelse når strømningen ligger i et område hvor friksjonskoeffisienten blir uavhengig av Reynolds-tallet. Skalaforhold for vannføring blir da: Qm/Qp = (Hm/Hp)0,5•y2
TI tillegg til forannevnte skaleringsformler vil man fra modell til prototyp ha skalaeffekt. Dette kommer som følge av at det ikke er mulig å lage en modell som i alle forhold gjenspeiler prototyps egenskaper. Generelt anerkjente normer for kvantifisering av skalaeffekt foreligger ikke. Kvalitativt er det på den annen side slik at skalaeffektens betydning øker når modelldimensjonene reduseres. Besparelser på modellsiden kan således skje på bekostning av resultatenes pålitelighet.
23 Litteratur
En liste over litteratur som kan være nyttig for den som ønsker å utdype sin kunnskap ifm. forhold presentert i dette dokument, er gitt nedenfor. Etter listen følger en kort omtale av de enkelte publikasjoner. Referansenummereringen overenstemmelser med referansene som er angitt som tidligere i dette dokument.
| Forfatter/redaktør. | Tittel | Utgiver | Referanse |
|---|---|---|---|
| Brekke, Hermod. | Reg. av hydr. str.maskiner | Vannkraftlab. | [1] |
| Brox, Gunnar. | Falltap i kraftverkstunneler | EnFO. | [2] |
| Hellesten, Mørtstedt. | Energi- og kjemiteknikk. | Yrkesopplæring | [3] |
| Hütte. | Des Ingenieurs Taschenbuch. | Ernst & Sohn. | [4] |
| Miller, D. S. | Internal Flow Systems. | Flowmaster. | [5] |
| Nielsen, Torbjørn K. | Dyn. dim. av vannkraftverk. | Sintef. | [6] |
| Streeter & Wylie. | Hydraulic Trancients. | McGraw-Hill. | [7] |
| Vinnogg, Leif. | Høytrykks tappeluker. | Sintef. | [8] |
| White, Frank M. | Fluid Mechanics. | McGraw-Hill. | [9] |
| Wickert & Schmaußer. | Stahlwasserbau. | Springer. | [10] |
| Øverli, Jan M. | Strømningsmaskiner. | Tapir. | [11] |
| IEC-Publicaton no 41. | IEC. | [12] |
| Nummer | Referanse |
|---|---|
| [1] | Kompendium i fag nr. 64176 ved NTNU. Fullstendig tittel: “Regulering av hydrauliske strømningsmaskiner”. Kompendiet gir en særdeles god oversikt vedrørende ulike transiente forhold som opptrer i et kraftverksystem og av hvordan disse vanligvis blir kartlagt. For lesere som ikke kjenner teorien fra tidligere, medfører enkelte mangelfulle symboloversikter at det kompendiet blir noe mer tunglest enn det det hadde behøvd å være. Kompendiet kan bestilles fra Vannkraftlaboratoriet, NTNU. |
| [2] | Rapport utgitt i 1985 av Vassdragsregulantenes forening, nå EnFO, i samarbeid med NHL, konsulenter og kraftselskaper. Rapporten vurderer tapsformler og sammenheng mellom hydraulisk tap og tunneloverflate. Den inneholder måledata og antyder hvilken overflatebeskaffenhet en byggherre bør kunne forlange av en entreprenør som skal lage en vanntunnel. Rapporten kan bestilles hos EnFO. |
| [3] | Tabellsamling benyttet av ingeniørskoler, inneholdende termodynamiske data som kan være til nytte ved analyse av luftstrømning ved høy hastighet. Tabellsamlingen kan bestilles i bokhandel. |
| [4] | Hütte I: “Teoretische Grundlagen”. Tysk ingeniørhåndbok. |
| [5] | Dokumentasjonsbok for det strømningstekniske databeregningsprogrammet “Flowmaster”. Boken inneholder bl.a. et stor utvalg av tapskoeffisienter for ulike rør systemelementer. I noen grad forutsetter boken at leseren på forhånd har strømningstekniske kunnskaper. Boken kan bestilles i bokhandel. |
| [6] | Rapport/kompendium som presenterer forenklede modeller og overslagsformler for sjaktsvingninger, trykk foran turbin ved store pådragsendringer samt reguleringsstabilitet. Teori er tatt med i den grad dette er nødvendig for leserens forståelse. Publikasjonen kan bestilles hos Kværner Energy, Trondheim (tidl. Sintef Strømningsmaskiner), rapportnr. STF67 A90038. |
| [7] | Lærebok i ikke-stasjonær med høyt faglig nivå. Boken kan bestilles i bokhandel. |
| [8] | Rapport publisert i 1973 av VHL, nå NHL, på oppdrag av en rekke kraftselskaper, konsulentfirma, lukeleverandører og konsesjonsavgiftsfondet etter at det ut gjennom 60-årene hadde inntruffet en rekke lukehavarier. Rapporten inneholder bl.a. anbefalinger for hydraulisk utforming av høytrykks tappeluker. Utforming med tanke på rasjonell produksjon, bruddmekaniske forhold og vedlikeholdsvennlighet er i mindre grad berørt. Rapporten kan bestilles hos NHL, rapportnr. STF60 A73041. |
| [9] | Lærebok i strømningsteknikk med høyt faglig nivå. Boken kan bestilles i bokhandel. |
| [10] | Bok med meget grundig gjennomgang av emnet kraftverksluker. I den strømningstekniske del inneholder boken tappekapasitetsdata for de fleste luketyper. Boken har i de senere år vært utsolgt fra forlaget. |
| [11] | Praktisk bok om strømningsteknikk og noen av det teoretiske grunnlag for strømningsmaskiner. Boken har vært benyttet ifm. grunnfag ved NTH samt som lærebok ved enkelte ingeniørhøgskoler. Boken er velegnet for innføring i enklere strømningstekniske teori. Boken kan bestilles i bokhandel. |
| [12] | Internasjonal “standard” for hydrauliske feltmålinger med hovedvekt på virkningsgradsbestemmelse for hydrauliske maskiner. “Standarden” angir imidlertid også prosedyrer som kan anbefales ved trykk- og vannføringsmålinger ifm. det øvrige utstyr i kraftverksvannveien. “Standarden” kan bestilles fra Norsk Elektrisk Komité (NEK). |
