HÅNDBOK - MEKANISKE KONSTRUKSJONER I VANNVEIEN: VEDLIKEHOLD AV UTSTYR I KRAFTVERKSVANNVEIEN
1 Innledning
Forfatter: Ragnar Hartmann, Statkraft Engineering as 04.01.96
Dette manuskript er betalt av Energiforsyningens Fellesorganisasjon (EnFO) og kan fritt benyttes ved alle EnFOs nåværende og fremtidige kurs. Bruk til andre formål, omarbeidelser eller videre bearbeiding, krever forfatters godkjennelse. Statkraft Engineerings eventuelle bruk av manuskriptet skal ikke skje slik at dette kommer i konkurranse med EnFOs virksomhet. Privatpersoner har anledning til å ta enkeltkopier når for- målet er egen opplæring. Ved kopiering ut over dette for andre enn EnFO, Statkraft Engineering eller forfatter, må tillatelse på forhånd være innhentet fra EnFO.
2 Hensikt og målsetting for dokument
Manuskriptet er laget i tilknytning til et kurs om luker, ventiler, rør og varegrinder. Målsettingen er å gi innblikk i ulik vedlikeholdssystematikk og enkelte forhold som kan være av betydning når større vedlikeholdsoppgaver skal utføres. Målgruppe er personell ved vannverk og i kraftforsyning.
3 Generelt om vedlikehold
Vedlikehold kan defineres som all aktivitet for opprettholdelse av et utstyrs eller konstruksjons funksjoner. Tilstandskontroll som gjennomføres ifm. planlegging og evaluering av vedlikeholdstiltak, forstås som del av vedlikeholdet.
Enkelte skiller mellom begrepene “vedlikehold” og “reparasjon”, og mange mener at det går en grense mellom “vedlikehold” og “rehabilitering”. I budsjettsammenheng kan det være praktisk å anse “vedlikehold” som det man skal gjøre hvert eneste år og som man trenger et fast budsjettet for. Reparasjoner kommer derimot ofte når man er minst forberedt på dette. Det kan derfor være greit å anse reparasjoner som noe spesielt det kan bes om tilleggsbevilgning for. Når det gjelder rehabiliteringer, forberedes disse over tid ved planlegging, prosjekt-/budsjettsøknad, etc. Ofte ser en på rehabilitering som investeringsprosjekt.
Det er således mange praktiske årsaker som taler for ulik behandling av vedlikehold, reparasjon og rehabilitering. På den annen side tilsier forannevnte definisjon at de alle bør oppfattes som vedlikehold. Aktivitetene er også koplet på slik måte at reduksjon i “Iøpende vedlikehold” etter hvert nødvendiggjør rehabiliteringer eller at man påføres et økende antall reparasjoner.
Oppsummeringsmessig kan det hevdes at fastleggelse av egentlige vedlikeholdsomkostninger bør gjøres ved helhetsvurdering hvor alt som skjer gjennom utstyrets/konstruksjonens levetid, blir inkludert. Stikkord er bl.a.: Vedlikeholdsreduserende tiltak ved utførelsen av utstyr/konstruksjon, vedlikehold, rehabiliteringer, reparasjoner, produksjonstap og levetid.
4 Vedlikeholdsstrategi
Holdninger til vedlikehold har variert over tid. Forholdet er søkt illustrert ved Figur 1. Her angis tre ulike epoker/perioder. Slik disse tidsmessig blir angitt i figuren, er de mer referert til tidlige implementeringstidspunkter i industrien generelt, mindre til de tidspunkter da metodene ble tatt i bruk av vannkraftbransjen og ved vannverk.
I Figur 1 angis “syn på feilutvikling” vha. kurver. Disse viser skjematisk sviktintensiteten zT(t), se manuskriptet “Sikkerhets- og pålitelighetsteknikk”. For tyngre konstruksjoner og utstyr i kraftverksvannveien er rådende teknisk oppfatning at objektenes sviktintensitet, forutsatt riktig vedlikehold, stort sett forblir konstant når de er kurert for “barnesykdommer”.
Det kan ellers hevdes vannkraftsektoren tidlig på 60-tallet tok til å bevege seg fra epoke I til epoke II. Sentralt sto utarbeidelsen og innføringen av “Helledal-systemet”. Dette bygget delvis på systemer utviklet for skipsfart.
At mange oppfattet Helledal-systemet som et “statisk system” for periodisk vedlikehold er å beklage. Skaperen av systemet, Oddvar Helledal var av den mening at rutinene skulle være underlagt kontinuerlig justering og tilpassing bestemt av høstede erfaringer. For Helledal var det heller ingen motsetning mellom hans system og “behovsprøvet vedlikehold, fastlagt ut fra periodisk tilstandskontroll”.
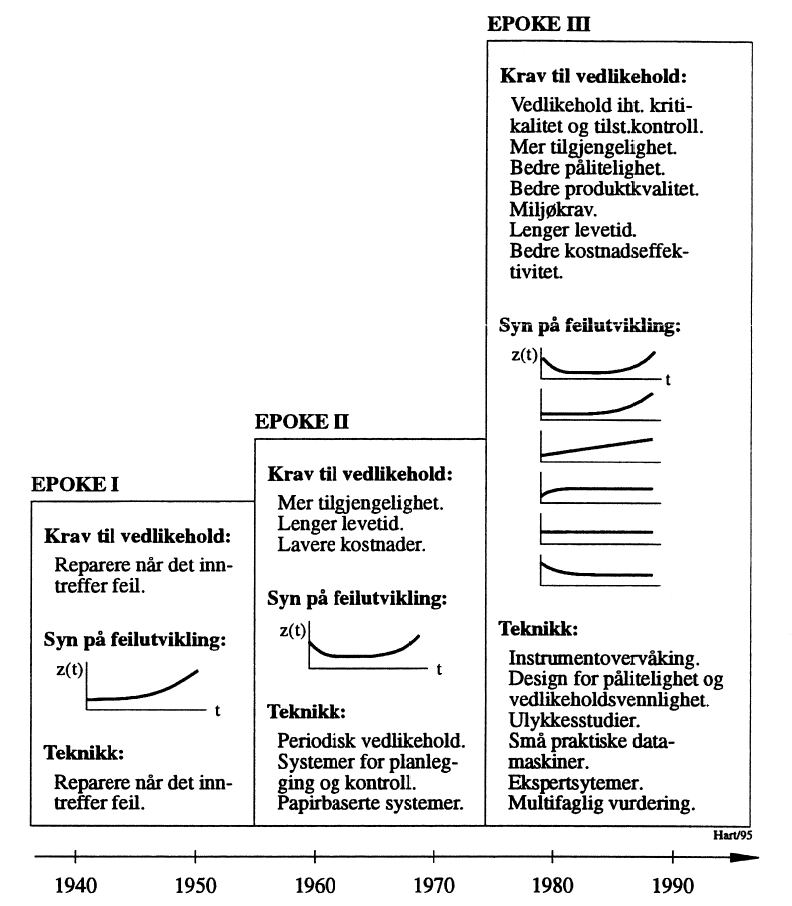
Selv om bransjen i en viss grad har “tenkt” i retning av epoke III siden begynnelsen på 80-tallet, kan man på mange måter si at man fortsatt er i overgangen fra epoke II til epoke II. Sentralt for strategien i epoke II blir bl.a. at-vedlikehold-utføres iht. kritikalitet. Dette betyr at man har skadepreventivt vedlikehold i den grad at dette anses nødvendig eller økonomisk ut fra vurdering av de skadeutviklinger og konsekvenser som må forutsettes når vedlikehold ikke utføres.
Det må imidlertid også antas at mange kraftverkseiere vil finne det tilfredsstillende å forbli i epoke II med et “modifisert” Heliedal-system. Det er nok også riktig at det man sparer ved å innføre et kritikalitetsstyrt vedlikehold, ikke alltid står ift. analysearbeidet som forut for kritikalitetsstyringen må utføres. Særlig gjelder dette for mindre anlegg.
5 Databasert vedlikeholdssystem
Fordelen med elektronisk databehandling ligger som kjent primært i det at man ved dette kan holde styr på og behandle store datamengder. Avgjørelser som fattes etter “råd fra datamaskin”, behøver imidlertid ikke være riktigere enn det man kommer frem til ved egen kompetanse og sunt vett. Ofte kan det bli tvert imot fordi det er en viss tendens til i mindre grad å stille spørsmål ved konklusjoner som kommer ut av et databasert “ekspertsystem”, enn det man ville gjøre om det var en person som sto for konklusjonene. Ekspertsystemer som forutsetningsvis skal være generelle, kan også “friste” til forenklinger som egentlig ikke burde blitt gjort.
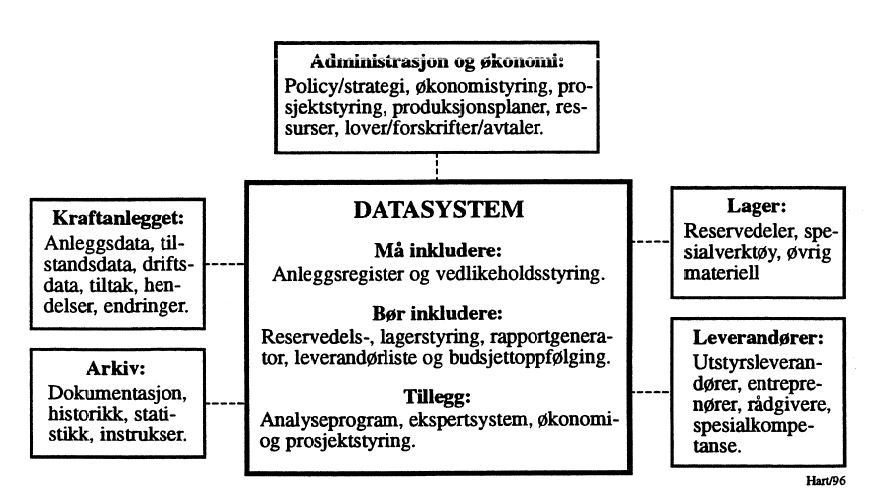
De første databaserte vedlikeholdssystemene ble tatt i bruk i kraftforsyningen på midten av 80-tallet. I sin enkleste form dreide dette seg om overføring av Helledal-systemet til EDB. En studie utført av Statkraft på denne tid konkluderte med at et databasert vedlikeholdssystem, uansett om kraftverksystemet det skulle dekke var enkelt eller komplekst, burde ha visse basiselementer. De viktigste basiselementene ble anleggsregister og vedlikeholdsstyring. Enkelte tilleggsdeler kunne dessuten med fordel inkluderes. Sentralt sto her reservedels- og lagerstyring. Tillegg omfattende analyseprogrammer og ekspertsystemer ble gitt lavere prioritet. Man anså også nødvendigheten av at vedlikeholdssystemet på en eller annen måte kunne koples opp mot andre eksisterende systemer i kraftverksdriften. Som “pakke” er dette forsøkt vist i Figur 2.
Erfaringer med datasystemer som ut fra nevnte kriterier er utviklet, har imidlertid vært noe blandede. Enkelte systemer ble eksempelvis for store ift. de anvendte datamaskiner. Dette medførte at systemene var trege i praktisk bruk, og at det ble irriterende mye ventetid foran dataskjermen.
6 Økonomisk riktig vedlikehold, formler
Som det fremgår av Figur 1 har det tidligere vært en utbredt oppfatning av at sannsynligheten for at en konstruksjon eller et utstyr svikter, øker med tiden. Skadeprosesser som gir slik feilutvikling, er utmatting og korrosjon. Få konstruksjoner i kraftverksvannveien er imidlertid utsatt for utmatting. Når det gjelder korrosjon, er det slik at man med seriøst korrosjonsvedlikehold på effektiv måte kan hindre uopprettelig forfall.
I mange tilfeller vil økonomiske beregning av riktig vedlikehold bli tvilsom. Med tanke på de tilfeller hvor slik beregning likevel er aktuell, kan det fremheves et par størrelser som slik beregning ofte inkluderer.
Har man ved en nyinstallasjon to mulige løsninger, en som er dyr i anskaffelse og har lave vedlikeholdsutgifter, og en som er billig i anskaffelse, men hvor vedlikeholdsomkostningene blir høye, er det nødvendig å vurdere vedlikeholdsomkostningene mot anskaffelsesprisen. For slik sammenligning beregnes nåverdien. Denne gis ved:
\[\text{Nåverdi = }\sum_{t=0}^T\space K_t\cdot (1+p)^{-t}\qquad{(1)}\]
Her er: - T: Utstyrets levetid angitt i år. - Kr: Utgift i år t. - p: Realrente, ofte 7 % (dvs. 0,07 innsatt i fomelen).
Er man interessert i å fordele alle utbetalinger etter et annuitetsprinsipp slik at årlige utgifter blir like (Kkonst), kan dette bestemmes ved:
\[K_{konst} = \text{Nåverdi}\cdot \frac{p}{1-(1+p)^{-T}}\qquad{(2)}\]
Aktuelle størrelser som inngår i beregningen av Kkonst, er som angitt i det foregående.
7 Optimalt rehabiliteringsintervall for kraftverksrør
Fremgangsmåten ved beregning av optimalt rehabiliteringsintervall for kraftverksrør belyses i det etterfølgende ved et eksempel.
Et kraftverksrør med innvendig diameter Ø3000 mm og lengde 350 m har i ny tilstand friksjonsfaktor λ lik 0,0073. Etter 30 år antas det at friksjonsfaktoren har økt til 0,0178. De aktuelle λ-verdiene tilsvarer analoge sandruheter på 0,008 mm og 1,9 mm.
Utviklingen av rørfriksjonen kan inndeles i to faser. I første fase nedbrytes malingfilmen. I fase 2 skjer det vekst av malingblærer/rustknoller. Dette gjør det aktuelt å velge en eksponentiell økning av de hydrauliske tap. Tapet i år t blir følgelig:
\[\Delta h_t = \Delta h_{t1} + (\Delta h_{t30}-\Delta h_{t1})\cdot (t/30)^m\qquad{(3)}\]
Med vannføring Q = 40 m3/s og eksponent m = 2,5 kan følgende beregnes:
Rørtverrsnitt: \[A_{tv.snitt} = \pi\cdot d^2/4=\pi\cdot 3,00^2/4=7,069\space\text{m}^2\qquad{(4)}\]
Innv. rørflate: \[A_{flate} = \pi\cdot d\cdot L=\pi\cdot 3,00\cdot 3,50=3299 \space\text{m}^2\qquad{(5)}\]
Strømningshastighet: \[v = Q/A=40/7,069=5,66 \space\text{m/s}\qquad{(6)}\]
Falltap i år 1: \[\Delta h_{t1} = \lambda \cdot (L/d)\cdot v^2/2g \newline =0,0073\cdot (350/3,00)\cdot 5,66^2/(2\cdot 9,81)=1,39 \space\text{mVs}\qquad{(7)}\]
Falltap i år 30: \[\Delta h_{t30}=\lambda\cdot (L/d)\cdot v^2/2g \newline =0,0178\cdot (350/3,00)\cdot 5,66^2/(2\cdot 9,81)=3,39\space\text{mVs}\qquad{(8)}\]
Falltap i år t: \[\Delta h_t = \Delta h_{t1} + (\Delta h_{t30}-\Delta h_{t1})\cdot (t/30)^m \newline =1,39+2,00\cdot (t/30)^{2,5}\qquad{(9)}\]
Er driftstiden n = 6200 timer pr. år, energiprisen kenergi = 15 øre/KWh og aggregatvirkningsgraden ηaggr=0,90 blir verdien av energitapet i år t (produksjonstapet):
\[K_t = k_{energi}\cdot \eta_{aggr}\cdot \rho\cdot g\cdot Q\cdot \Delta h_t\cdot n \newline =(0,15/1000)\cdot 0,90\cdot 1000\cdot 9,81\cdot 40\cdot (1,39+2,00\cdot (t/30)^{2,5})\cdot 6200 \newline = 328400\cdot (1,39+2,00\cdot (t/30)^{2,5})\qquad{(10)}\]
År 1 forutsettes å starte med korrosjonsbehandling av røret. Er enhetsprisen for behandling kmaling=500 kr/m2, kan total behandlingspris beregnes til:
\[K_{beh} = k_{maling}\cdot A_{flate}=500\cdot 3299 = \text{1 650 000 kr}\qquad{(11)}\]
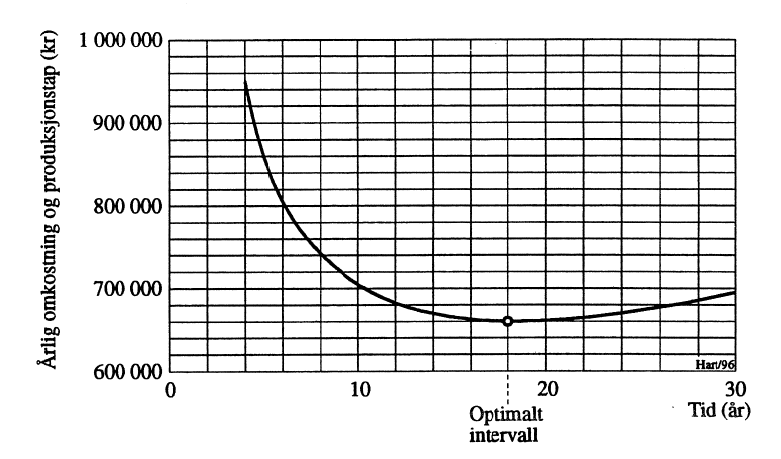
Nåverdi av behandlingspris og alle energitap over periode m år kan etter dette beregnes iht. formelen i Kapittel 5. Denne fordeles etter annuitetsprinsippet over årene i perioden, se uttrykk for Kkonst i Kapittel 5. Beregningene gjøres i regneark med m som variabel og 7% realrente. Den verdi av m som gir lavest Kkonst, blir følgelig det optimale rørrehabiliteringsintervallet. Resultatet av beregningen er vist grafisk i Figur 3. Som det fremgår bestemmes optimalt intervall til 18 år. Av figuren ser en også at det i dette tilfellet får liten økonomisk betydning om intervallet forlenges til 22-24 år.
Som kommentar til beregningen kan det påpekes at ruhetsutviklingen som i dette tilfellet er bestemmende for tapets tidsfunksjon, her er større enn det man forventer for dagens godkjente korrosjonsbeskyttelsesbelegg.
8 Vurderinger ifm. korrosjonssvekket luke
På samme måte som ved gjennomgangen av optimalberegning for rørrehabiliteringsintervall i Kapittel 7, vil en også eksemplifisere problemstillinger ifm. en korrosjonssvekket luke. Dette gjelder tappeluke i overføringstunnel mellom to kraftverksmagasiner. Motforestillinger ifm. de anvendte metodene blir drøftes.
Luken er vanskelig tilgjengelig for vedlikehold. Den har vært i drift i 60 år uten at vedlikehold er utført på lukekonstruksjonen. For luken da den var ny, antas det sannsynlighet for alvorlig funksjonssvikt i ikke tilgjengelige struktur og innen tidsintervallet 1 år, tilsvarende 10-5. I dagens situasjon med nåværende tilstand er antagelsen at nevnte sannsynligheter 3•10-2.
Med henvisning til manuskriptet “Sikkerhets- og pålitelighetsteknikk” kan muligheten for svikt innenfor tidsrommet At ved tiden t tilnærmet uttrykkes som: Δt•zT(t). Uttrykket forutsetter at Δt er liten. Antas det Weibulls feilfordeling, en fordeling som er anbefalt be- nyttet ved denne type problem, gjelder for tidsintervall Δt lik tidsenheten 1 år.
\[z_T(1)=\alpha\cdot \lambda\cdot (\lambda\cdot 1)^{\alpha-1}=10^{-5} \newline z_T(60)=\alpha \cdot \lambda \cdot (\lambda\cdot 60)^{\alpha-1}=(10^{-5}/\lambda^{\alpha-1})\cdot (\lambda\cdot 60)^{\alpha-1}=3\cdot 10^{-2}\qquad{(12)}\]
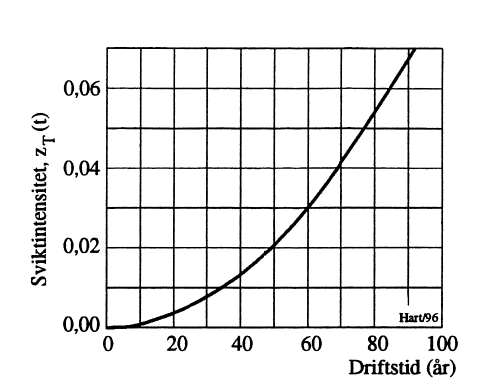
Løsning gir α=2,956 og λ=0,01410 med sviktintensitetsfunksjon som uttrykt på neste side og grafisk fremstilt i Figur 4.
\[\text{Sviktintensitet:}\hspace{1cm}z_T(t)=2,956\cdot 0,01410\cdot (0,01410\cdot t)^{(2,956-1)}=10^{-5}\cdot t^{1,956}\qquad{(13)}\]
Aktuelt vedlikeholdstiltak forutsettes å koste 6 mill. kroner. Ved alvorlig svikt blir summen av produksjonstap og tiltak 100 mill. kroner. Hevdes det at “siste” tidspunkt for å gjennomføre vedlikeholdstiltak er når risikoen ifm. alvorlig svikt tilsvarer vedlikeholdsomkostningen, blir:
\[\text{100 000 000}\cdot 10^{-5}\cdot t^{1,965}=\text{6 000 000}\hspace{1cm}\text{Utregnet: }\space t=85\space \text{år}\qquad{(14)}\]
I en tidsskriftartikkel beskrives en lignende beregning av dir. Otto Hartmann ved Motor Columbus Consulting Engineers, gjeldende vurdering av elektriske generatorer. Her tas det utgangspunkt i en “fysisk levetid” T. For ny maskin settes havarisannsynligheten lik k0. Ved t = T er kT = 100 %. For 0 < t < T defineres k(t) som eksponentiell funksjon, og vedlikeholdstidspunktet hevdes gitt ved: Kvedlikeh.=k(t)•Khavari
Når det gjelder forannevnte lukeproblem, har man tilsynelatende kommet til at luken fortsatt kan benyttes i 25 år uten vedlikehold. Til dette blir innvendingene:
Muligheten for alvorlig svikt vil i år 85 være 0,06. Dette er vesentlig mer enn det som aksepteres av sviktmulighet for tungt vannkraftutstyr. Eksempelvis må det nevnes at årlig gjennomsnittlig rørbruddsmulighet for smisveiste rør har vært i overkant av 0,002. Etter oppfatningen til det offentlige tilsynsorgan, NVE, er 0,002 for kraftverksrør en uakseptabel høy sviktsannsynlighet. Det kan ut fra dette neppe anses akseptabelt at en luke får en sviktsannsynlighet som er 30 ganger større.
Det er betydelig usikkerhet knyttet til forutsetningen av at sviktsannsynligheten i lukens 85. driftsår ikke overskrider 0,06. Ut fra praktisk erfaring kan det også synes som om Weibull-fordelingen gir for stor økning av sviktintensiteten i de første driftsår, og at økningen etter 60 år skulle vært større.
Oppstår det alvorlig svikt, påføres eieren et tap på 100 mill. kroner. Det er ikke gitt at eieren har økonomisk evne til å tåle dette.
I beregningen er det benyttet havaririsiko referert til tidsintervallet Δt = 1 år. Med annet tidsintervall blir også “sistetidspunktet” et annet.
Vanlig praksis fra norsk vannkraftmiljø vil imidlertid her, for nevnte luke, tilsi at de nødvendige vedlikeholdstiltak gjennomføres forholdsvis umiddelbart, etter en normal planleggingsprosedyre, men uten unødige forsinkelser.
Sistnevnte konklusjon kan støttes av de forannevnte matematiske forutsetninger. Faktum er at luken med angitte feilfordeling har hatt en sannsynlighet for å “overleve” 60 års drift gitt ved:
\[R_T(60)=e^{-(\lambda\cdot 60)^{\alpha}}=e^{-(0,0141\cdot 60)^{2,956}}=e^{-0,610}=0,54\qquad{(15)}\]
Det har med andre ord vært 46 % sannsynlighet for at luken allerede skulle ha havarert. Levetid settes dessuten ofte i “pålitelighetsfaget” lik MTTF (mean time to failure). Med Weibull-fordeling er det noe komplisert å beregne MTTF, men tiden t = λ-1 som blir den tid det er 37 % sannsynlighet for å overleve, avviker vanligvis mindre enn 10 % fra MTTF.
\[\text{MTTF = }\lambda^{-1}\pm10\%=0,0141^{-1}\pm10\%=71\pm7\text{ år}\qquad{(16)}\]
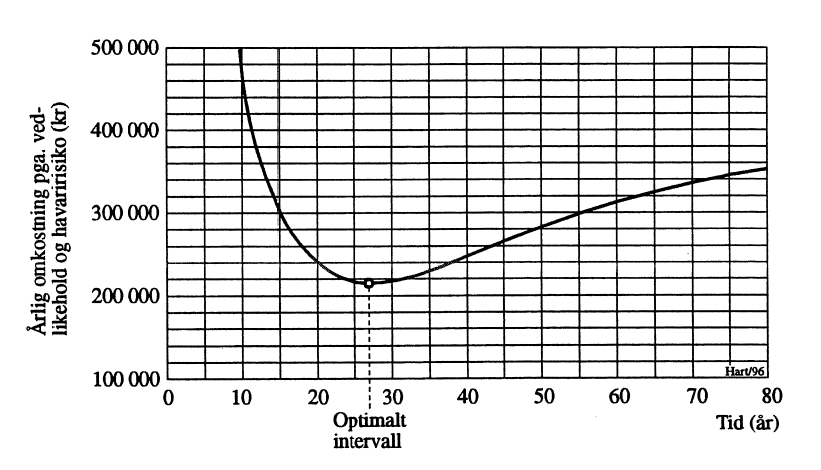
Videre kan man også nærme seg problemet ved å bruke tilsvarende betraktning som vist i Kapittel 7. Jevnt fordelte omkostninger K for en rehabiliteringsperiode fra t = 1 år til t=T gis da av ligningen i det etterfølgende. Resultatet av regnearkberegning med forannevnte tallverdier for å bestemme minimumsverdien av K, fremgår av Figur 5.
Innvendingen mot dette er at man etter feilfri drift i 27 år som fremkommer som det optimale tidspunkt for tiltak, ikke har hatt havariomkostningene som reelle utgifter. Beslutter man seg imidlertid for å anvende luken ett år til uten vedlikeholdstiltak, er sannsynligheten for havari i dette året 0,0068. Risikoen tilsvarer da 680 tusen kroner. Dette kan sammenholdes med ett års utsettelse av rehabiliteringen, hvilket gir en rentegevinst på kun 420 tusen kroner.
9 Praktiske vedlikeholdsoppgaver
Vedlikeholdsoppgavene varierer fra utstyr til utstyr. Enkelte hovedoppgaver kan midlertid fremheves.
| Grinder: | Rengjøring for å redusere falltap, korrosjonsbeskyttelse, eventuell utbedring av utmattingsskader. |
| Rør: | Rengjøring av utvendige flater for å hindre korrosjon eventuelt råte, korrosjonsbeskyttelse, rengjøring og utskifting av tetninger i ekspansjoner hvis lekkasje, oppretning av rørfundamenter hvis setninger / svikt. |
| Luker: | Rengjøring for å hindre korrosjon / slitasje / uakseptabel friksjon, smøring, fjerning av fremmedlegemer som kan hindre manøvrering, korrosjonsbeskyttelse, utskiftning av luketetninger hvis lekkasje. |
| Ventiler: | Stort sett tilsvarende luker. |
Ofte kan omkostningene ved forberedelser, riggearbeider, etc. bli betydelige. Stikkord i denne sammenhenger: Planlegging m/ valg av løsning, etablering av avstenging, produksjonstap ved ev. senking av magasin og manglende produksjonstilgjengelighet, helikoptertransport, bygging av adkomster (eksempelvis taubane), arbeidsstillinger, ventilasjons og avfuktingssystemer, pumpeanlegg.
Korrosjonsbeskyttelse går igjen for samtlige utstyr. For dette benyttes hovedsakelig korrosjonshindrende belegg. Mangeårige erfaringer gir i denne sammenheng grunn for å understreke de forhold som er listet på neste side.
Selgere av korrosjonsbeskyttende belegg kjenner ofte ikke vannkraftbransjens krav og lover til tider mer enn det produktene tilfredsstiller. Det er derfor en god regel å holde seg til utprøvde produkter som en har god erfaring med. Aktuelt krav til belegg har ellers vært feilfrihet etter ett års eksponering i kondenskammer. Regelen er at ansvaret for å kunne dokumentere at et produkt tilfredsstiller dette, påligger utførende korrosjonsentreprenør.
Det hender at malingsprodusenter endrer resepten for sine produkter uten at dette fremgår av produktenes tekniske dokumentasjon. Ved alle større korrosjonsvedlikeholdsarbeider bør derfor anleggseieren holde av utørket/uherdet prøve av hver anvendt “produksjons-batch” med tanke på eventuelle garantispørsmål.
Nye produkter til tross, har man dårlig erfaring med maling på våt eller ikke rengjort flate. Standardkravene som tilsier blåserensing til minst Sa 2,5 og at ståltemperaturen skal ligge minst 3 °C over luftens duggpunktstemperatur, må ikke fravikes. For herdende belegg er det dessuten viktig at ståltemperaturen også er høyere enn den minimumstemperatur hvor tilfredsstillende utherding kan skje for det angjeldende produkt. For mange herdende belegg er denne +10 °C. Generelt bør det aldri heller males med ståltemperatur under 0 °C. Rensemetoder som stålbørsting, etc. frarådes det at man aksepterer.
Ved viktige korrosjonsbeskyttelsesarbeider må det alltid stilles faglige krav til utførende personell. Relevant fagutdannelse og/eller sertifiseringsordning eksisterer ifm. så vel blåserensing og malingpåføring som inspeksjonsvirksomhet.
For korrosjonsbeskyttende belegg har vannkraftbransjen utarbeidet en “malingspesifikasjon”. Denne bør legges til grunn ved ethvert større korrosjonsvedlikehold.
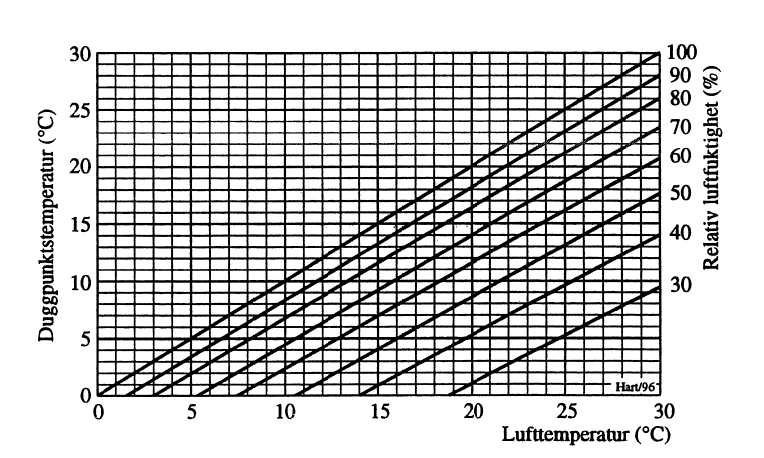
Vedr. kravet til ståltemperatur ift. duggpunkt, kan det bemerkes at duggpunktet bestemmes som funksjon av luftens temperatur og relative fuktighet. Disse to størrelser må måles på ett og samme sted. Funksjonssammenhengen mellom temperatur/fuktighet og duggpunkt fremgår av Figur 6.
